An Improved Radiative Transfer Model for Polarimetric Backscattering from Agricultural Fields at C- and X-Bands

Article information

J. Electromagn. Eng. Sci. 2021;21(2):104-110

Publication date (electronic) : 2020 April 30

doi : https://doi.org/10.26866/jees.2021.21.2.104

Yisok Oh ¹^,, Jisung Geba Chang ², Maxim Shoshany ²

¹School of Electronic and Electrical Engineering, Hongik University, Seoul, Korea

²Faculty of Civil & Environmental Engineering, Technion - Israel Institute of Technology, Haifa, Israel

^*Corresponding Author: Yisok Oh (e-mail: yisokoh@hongik.ac.kr)

Received 2020 July 23; Revised 2020 October 20; Accepted 2020 November 3.

Abstract

The first-order vector radiative transfer model (FVRTM) is modified mainly by examining the effects of leaf curvature of vegetation canopies, the higher-order multiple scattering among vegetation scattering particles, and the underlying-surface roughness for forward reflection on radar backscattering from farming fields at C- and X-bands. At first, we collected the backscattering coefficients measured by scatterometers and space-borne synthetic aperture radar (SAR), field-measured ground-truth data sets, and theoretical scattering models for radar backscattering from vegetation fields at microwaves. Then, these effects on the RTM were examined using the database at the C- and X-bands. Finally, an improved RTM was obtained by adjusting its parameters, mainly related with the leaf curvature, the higher-order multiple scattering, and the underlying-surface small-roughness characteristics, and its accuracy was verified by comparisons between the improved RTM and measurement data sets.

Keywords: Backscattering Coefficient; Leaf Curvature; Multiple Scattering; Radiative Transfer Model; Surface Roughness

I. Introduction

Microwave remote sensing of Earth’s terrain using satellite synthetic aperture radar (SAR) provides us valuable information nowadays. There are many SARs at C- and X-bands, such as SENTINEL-1(A and B) and RADARSAT-2 at the C-band and TerraSAR-X/TanDEM-X, COSMO-SkyMed(1, 2, 3, 4), and KOMPSAT-5 at the X-band. Therefore, in this study we focused on the C- and X-bands, and also on farming fields and rangelands that microwaves at C- and X-bands can penetrate through their vegetation canopies.

The radiative transfer (RT) technique has been widely used for microwave backscattering from vegetation fields [1, 2]. The radiative transfer model (RTM) has a relatively good accuracy for estimating the backscattering coefficients for a wide range of vegetation canopies [3, 4]. In the RTM, the phase matrix should be accurately calculated for a scattering particle with given incident, scattered, and orientation angles in elevation and azimuthal directions (θ_i,φ_i; θ_s,φ_s; θ_p,φ_p) as well as the size of the particles relative to the wavelength [1].

The phase matrix is obtained from a scattering matrix [S] that is calculated assuming that a leaf is a dielectric lossy flat rectangular or circular plate. The RTM may need to be examined further in terms of the effect of the curvature of a leaf on the radar backscatter to be more practical for applying this model to the determination of the backscattering coefficients of vegetation canopies. The effect of curvature on the radar backscatter is quite large for backscattering from a curved dielectric sheet at C- and X-band frequencies [5, 6]. Therefore, we may need to examine in detail the effect of the leaf curvature on the RTM.

The first-order vector RTM does not include the higher-order multiple scattering among scattering particles in a vegetation canopy. The cross-polarized backscattering coefficient (

σvh0 or σhv0) of a vegetation field is much more sensitive to the multiple/volume scattering from a vegetation canopy than the co-polarized backscattering coefficients ( σhh0 and σvv0), and consequently, σvh0 is used for calculating the radar vegetation index (RVI) or polarimetric radar vegetation index (PRVI) [7]. It was also shown with a numerical calculation that the cross-polarized backscattering coefficient is very sensitive to the higher-order multiple scattering, whereas the co-polarized coefficients are not [8]. Therefore, the reexamination of the multiple-scattering effect on the RTM might be crucial, especially for the cross-polarized backscattering coefficients of vegetation fields.

Although the backscattering from a bare soil surface can be accurately computed with theoretical and empirical models such as the integral equation method (IEM) [9] and polarimetric radar inversion for soil moisture (PRISM) [10], the reflection from a rough soil surface needs to be examined in more detail, because the microwave interaction between the vegetation canopy and the underlying soil surface mainly depends on the soil-surface roughness in addition to the soil moisture. We may need to redefine the surface roughness for microwave reflection in a different scale (small roughness) in comparison with the surface roughness for microwave backscattering (large roughness).

In this paper, we first examine the RTM for the effect of the leaf curvature in a vegetation canopy, the multiple-scattering effect for vv-, hh-, and vh- (hv-) polarization combinations, and the effect of the surface roughness on the reflection coefficient of an underlying soil surface. Then, the RTM is modified with the optimized input parameters in relation with the leaf curvature, the higher-order multiple scattering, and the small roughness of underlying surface. Finally, the accuracy of the modified RTM is verified by comparing it with experimental data sets.

II. Examination of RTM

The first-order RTM is a well-known theoretical model for radar backscattering from a vegetation canopy over an underlying soil surface, especially for range and farming fields, as shown in Fig. 1. In general, the RTM includes five scattering mechanisms:

Fig. 1

Scattering mechanisms in FVRTM model.

(1) the direct backscatter from the vegetation layer,
(4) the direct backscatter from the underlying soil surface with the attenuation through the vegetation layer, and
(2)–(3) the interactions between the vegetation layer and the underlying soil surface: i.e.,
(2a) incidence – reflection from the ground – forward scattering from the vegetation layer – backscatter,
(2b) incidence – forward scattering from the vegetation layer – reflection from the ground – backscatter, and
(3) incidence – reflection from the ground –backscattering from the vegetation layer – reflection from the ground – backscatter.

Then the backscattering coefficient of a vegetated surface can be computed by the following summation of the five scattering mechanisms:

(1) σpqo=σvo+σgvo+σvgo+σgvgo+σgo,

where the first four terms can be formulated with scattering matrices of vegetation particles such as lossy dielectric disks for leaves and lossy dielectric cylinders for stems and branches [1–3]. The last term of Eq. (1) can be obtained from a theoretical or empirical model for microwave backscattering from soil surfaces [9, 10].

Eq. (1) can be explicitly expressed in the following form:

(2) σpqo=4π cos θ0 Tmn,

where p or q denotes v- or h-polarization, m or n is 1 or 2, and vv-, vh-, hv-, and hh-polarizations correspond to 11, 12, 21, and 22 elements of the 4×4 transformation matrix T¯¯ that can be computed with the following matrix multiplications with the canopy scattering matrix A¯¯, the eigen matrix E¯¯, the diagonal extinction matrix D¯¯, the reflectivity matrix R¯¯, the Stokes scattering operator matrix M¯¯, and the phase matrix P¯¯ [1, 5].

(3) T¯¯=∑k=15secθ0T¯¯kwithT¯¯1=E¯¯4 A¯¯41 E¯¯1-1 T¯¯2=E¯¯4 A¯¯42 E¯¯2-1R¯¯ {E¯¯1 D¯¯1 E¯¯1-1} T¯¯3={E¯¯4D¯¯4E¯¯4-1}R¯¯ E¯¯3 A¯¯31 E¯¯1-1 T¯¯4={E¯¯4D¯¯4E¯¯4-1}R¯¯ E¯¯3 A¯¯32 E¯¯2-1R¯¯ {E¯¯1D¯¯1E¯¯1-1} T¯¯5={E¯¯4D¯¯4E¯¯4-1}M¯¯{E¯¯1D¯¯1E¯¯1-1},

where [A¯¯kl]ij=[E¯¯k-1P¯¯klE¯¯l]ij Ckl,ij [4].

The subscripts k = 1, 2, 3, 4, and 5 of the transformation matrix T¯¯k correspond to the scattering mechanisms 1, 2a, 2b, 3, and 4, respectively, in Fig. 1. The subscripts 1, 2, 3, and 4 of other matrices indicate the scattering or incident directions (↘), (↗), (↙), and (↖), respectively. The 4×4 phase matrix P¯¯ can be computed from the 2×2 scattering matrices S¯¯ of scattering particles, and the constant C_kl,ij can be obtained using the averaged scattering matrices 〈 S¯¯〉, for the ij^th elements of the matrices. The Stokes scattering operator matrix M¯¯ can be computed from a polarimetric theoretical or empirical surface scattering model for backscattering coefficients, such as the IEM model and the PRISM model [2].

1. Effect of Leaf Curvature

There are various shapes and sizes of leaves in rangelands and farming fields, such as blade-type and disk-type lossy dielectric leaves. Those natural and agricultural leaves usually have curved shapes and/or irregular surfaces. The reduction of radar cross section (RCS σ) of a curved dielectric sheet can be analytically computed accurately by multiplying a curve factor to the scattering matrix of a flat dielectric disk, using a Fresnel integral with the argument of leaf length a and the radius of curvature ρ for a given frequency [6].

(4) Sc=Sfp F(γ)/γ, with γ=a2k0ρ,

where S_c is the scattering matrix element for a curved lossy dielectric sheet, S_fp is the scattering matrix element for a flat plate, F(γ) is the Fresnel integral with an argument γ, and k₀ is the wavenumber. For example, the reductions of RCS at normal incidence are about 0.98, 0.75, and 0.4 in magnitude for L-, C-, and X-bands, respectively, when both the curvature radius and leaf length are 6 cm. The RCS reductions are 0.95, 0.75, and 0.32 for the curvature radii of 12, 6, and 3 cm, respectively, with a fixed leaf length of 6 cm at the C-band [6]. Therefore, we need to multiply a multiplicative factor, i.e., the “curve factor” C_factor, to the scattering matrices for leaves and stems to compensate for the RCS reduction because of the leaf-curvature effect in the RTM.

(5) Cfactor≡〈ScSfp〉=〈F(γ)/γ〉,

(6) [S]m=Cfactor [S],

where [S]_m is the modified scattering matrix of a leaf or a branch.

The curve factor may also cover the RCS reduction that would be caused by the irregularity deviating from the flatness of a leaf.

2. Effect of Multiple Scattering

The RTM does not include the higher-order multiple scattering as shown in Fig. 1, whereas the actual microwave backscatter will include the higher-order multiple scattering inside the vegetation layer and between the vegetation layer and the underlying ground surface. A full-wave analysis by the moment method for a relatively sparse vegetation field revealed that the effect of multiple scattering is negligible for co-polarization, whereas the cross-polarized backscattering coefficients are significantly influenced by the effect of multiple scattering [8]. For example, the difference between a full-wave analysis that includes all orders of multiple scattering and a theoretical model that includes only single scattering is about 9 dB for hv-polarization and less than 0.5 dB for hh-polarization for a sample vegetation canopy with only ten 2λ-length stems on a 2λ-diameter underlying surface [8]. The fully phase-coherent computation [11] for the backscattering coefficients of grasslands also showed that the higher-order scattering terms should be added to fit the radar measurements for the cross-polarized data [12].

The effect of multiple scattering can be accounted by multiplying a factor, the so-called “multiple factor” M_factor, to the transformation matrix elements for the higher-order multiple scattering from scatters in a vegetation layer.

(7) [T]km=Mfactor,k[T]k,

where [T]_km is the modified k^th transformation matrix, and the multiple factor may be obtained from an extensive database of experimental measurements.

3. Effect of Surface Roughness

For the backscattering from an underlying soil surface, the microwave radiates from an antenna of a radar far from the rough surface. Therefore, the surface roughness should be considered for the whole antenna footprint that provides a largescale roughness. However, for the reflection from the underlying soil surface in the scattering mechanisms 2a, 2b, and 3 in Fig. 1, the scattering particles are positioned near the surface. Therefore, the area of reflection might be small, which provides a small roughness. The retrieval of the RMS height depends on the length of the surface profile, and the measured RMS height rapidly decreases with a decrease in the profile length of the surface [13, 14]. Therefore, the use of large-scale roughness parameters for mechanism 4 and small-scale roughness parameters for mechanisms 2a, 2b, and 3 can be recommended.

The effect of small roughness would be implemented with the decrease in the RMS height for the computation of the microwave reflection, such as h_RMS_–_s = roughness factor (R_factor)×h_RMS, where h_RMS_–_s is the small-roughness RMS height for reflection, and h_RMS is the RMS height for backscattering from the soil surface. For the reflection from a rough surface, the following form of the reflection coefficient is used for the reflectivity matrix.

(8) [R]m=Rmult [R],

where [R]_m is the modified reflectivity matrix, and

(9) Rmult=[ΓspΓfp]2=[exp[-X] I0[X]]2

with X=2(kh_RMS_–_scosθ)², where Γ_sp is the reflection coefficient of a rough soil surface, Γ_fp is the Fresnel reflection coefficient of a flat plane, the subscript p is the polarization, θ is the incidence angle, and I₀[···] is the modified first-kind Bessel function.

III. Modification and Verification of RTM

The parameters of the RTM with regard to the effects of the leaf curvature, multiple scattering, and small roughness can be determined on the basis of comparisons between the measurements and the RTM. There are numerous data sets for radar backscattering coefficients of vegetation fields at the C- and X-bands. However, it is difficult to find the ground-truth data sets that include all input parameters of the RTM, such as the water contents of leaves and stems, the root-mean-square (RMS) height of the underlying soil surface, the volumetric soil moisture content, the height of the vegetation-crown layer, and the averages and standard deviations of leaf length, leaf width, leaf density, leaf thickness, leaf vertical and horizontal angles, stem length, stem diameter, stem density, and stem vertical and horizontal angles. Therefore, we collected the ground-truth data in relation with the input parameters of the RTM as well as polarimetric scatterometer measurement data sets.

1. Experimental Data Sets

The Hongik polarimetric scatterometer (HPS) was used to acquire the full-polarimetric backscattering coefficients of vegetation fields to closely examine the RTM. The backscattering coefficients of a cornfield in Suwon, Korea, were acquired at the C-band and five different incidence angles (20°, 30°, 40°, 50°, and 60°) from May 29 to July 11, 2013, covering a whole growing season. The HPS is a vector-network-analyzer-based full-polarimetric L-, C-, and X-band scatterometer, and it is calibrated by the differential Mueller matrix calibration technique (DMMCT) [15] with a single calibration target, namely, a trihedral corner reflector. The backscattering coefficients of a bean field in Suwon, Korea, were also collected by the COSMO-SkyMed SAR at the X-band at 40° for hh-polarization during the bean growth cycle from July 22 to September 24, 2010.

We also collected in situ measured ground-truth data for all the input parameters of the RTM on the same days when the radar data were collected. The parameters for vegetation fields were obtained by sampling. The surface roughness parameters such as the RMS height were obtained from surface profiles that were measured with a laser profilometer and a pin profilometer. The leaf-area index (LAI) values were acquired using AccuPAR LP-80 of Decagon Devices Inc., and the soil moisture contents were measured using EC-5 of the same company.

2. Determination of Parameters

By minimizing the root-mean-square error (RMSE) between the RTM and the scatterometer measurements of a cornfield at the C-band, we can obtain optimum curve, multiple, and roughness factors. It was found that the optimized curve factors for considering the effect of leaf curvatures are about 0.7 for leaves and 1.0 for stems at the C-band for scattering from cornfields. The curve factor depends on frequency (or wavelength) [6], and the curve factor becomes about 0.5 for leaves and 0.7 for branches (stems) at the X-band for scattering from soybean fields.

The co-polarized backscattering coefficients that were measured from vegetation fields agree well with the RTM, and consequently, the multiple factor is about 1.0 at vv- and hh-polarizations as determined by the RMSE technique while considering the effect of multiple scattering, which means that the first-order multiple scattering is dominant for the co-polarized backscattering coefficients. However, the RMSE technique provides about 50 for the cross-polarized scattering from the corn fields.

The RMSE technique leads us to the rough factor of about 0.7. The effect of the rough factor is negligible for very sparse and very dense vegetation canopies, because the interaction between the vegetation canopy and the underlying surface in these cases is negligible.

3. Verification

The RTM is modified with the induced parameters from the effects of the leaf curvature, multiple scattering, and small roughness for the reflection, and its accuracy is examined by comparisons between the modified RTM and the scatterometer measurements. Fig. 2 shows the comparison among the scatterometer measurements on May 29, the traditional RTM (“Old Model”), and the new RTM modified with the “curve factor,” “multiple factor,” and “roughness factor” as explained in the previous section, and with in situ field-measured 21 input parameters, for multi-polarized backscattering coefficients of the cornfield. The early-stage cornfield on May 29, 2013 was a sparse vegetation field with a plant height of 30 cm and an LAI of 0.48. The backscattering from the underlying soil surface would be dominant in this case. Therefore, the improvement of the modified RTM is minimal for co-polarized backscattering coefficients. However, the cross-polarized backscattering coefficient of the modified RTM is remarkably improved, such as 2.2 dB at 50° and 4.4 dB at 60° as shown in Fig. 2.

Fig. 2

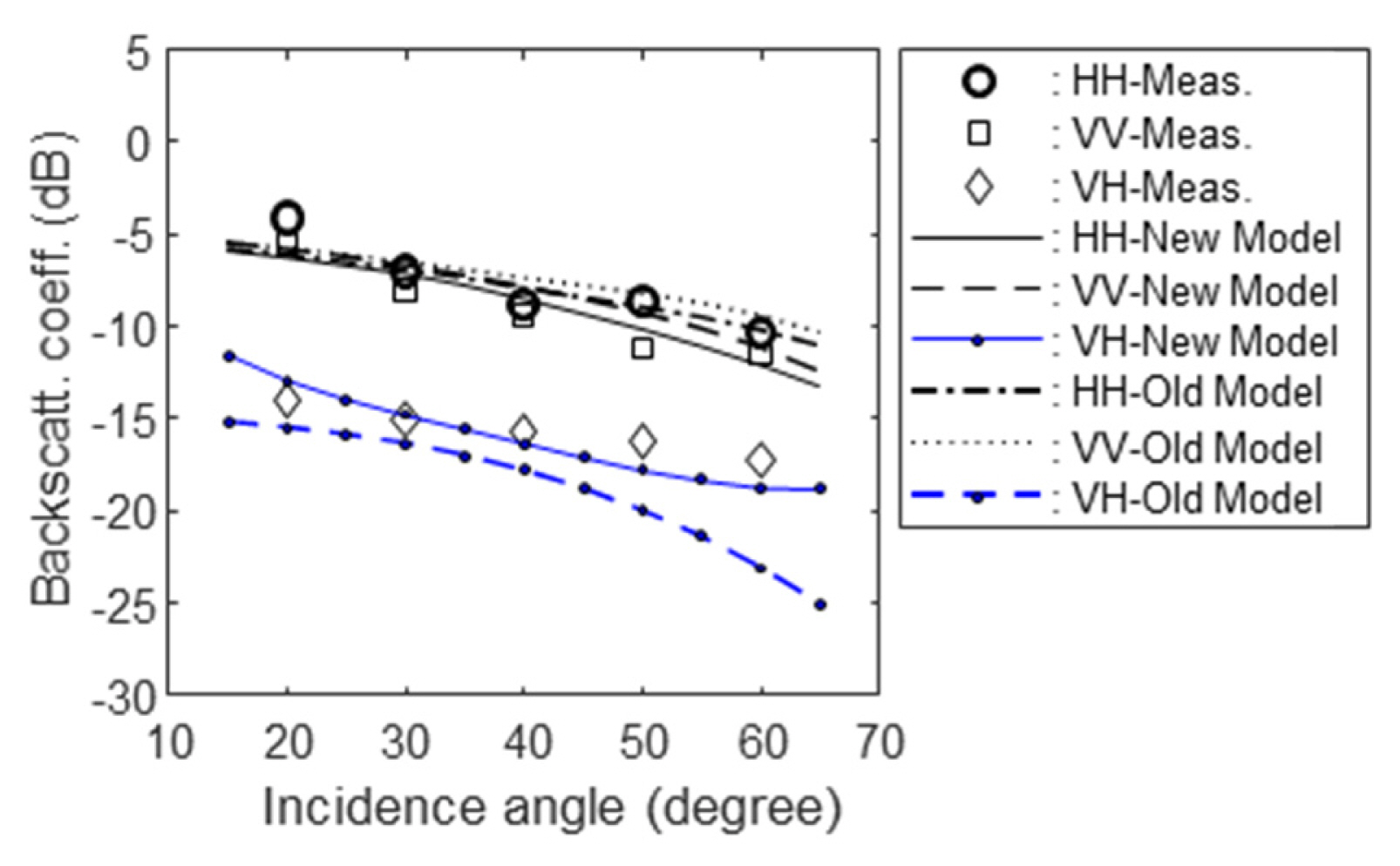
Comparison among HPS measurements on May 29, 2013, traditional RTM, and modified RTM for vv-, hh-, and vh-polarizations.

Fig. 3 shows the comparison among the scatterometer measurements on July 11, 2013, the traditional RTM, and the modified RTM for the multi-polarimetric data. The full-grown cornfield on July 11 was a dense vegetation field with a plant height of 250 cm and an LAI of 2.62. Fig. 3 shows that the traditional RTM provided about 2–3 dB higher co-polarized backscattering coefficient than the radar measurements without correction for the effect of leaf curvature, whereas the modified model and the measurements agree quite well for the co-polarized backscattering coefficients. The improvement of the cross-polarized backscattering coefficients with the modification for the higher-order multiple scattering is very large as shown in Fig. 3 and Table 1, especially for higher incidence angles, because of (1) the vertical structures of the corn-plant stems and (2) the effective depth increase at higher incidence angles. The discrepancy between the measurements and the modified RTM for vh-polarization at low incidence angles, especially 20° and 30°, may be from the fact that the RTM inherently does not include the shape and location of the full-grown leaves.

Fig. 3

Comparison between HPS measurements on July 11, 2003, traditional RTM, and modified RTM for multi-polarized data.

Table 1

Comparison of RMS deviations

The modified RTM is also compared with the COSMO-SkyMed data at the X-band, which were acquired from a bean field in Suwon, Korea, at 40° for hh-polarization during the bean growth cycle from July to October 2010. The ground-truth data were also collected in situ during the period for about two dozens of input parameters of the RTM. The LAIs of the bean fields were 0.73, 2.42, 3.21, 3.36, and 4.54 for 22, 37, 53, 70, and 86 days after planting, respectively. Fig. 4 shows the comparison between the COSMO-SkyMed data and the modified RTM for the bean field in a growing season. In this comparison, we used a curve factor of 0.5 for leaves and a curve factor of 0.7 for branches and stems, which are lower than the factors at the C-band, because the RCS reduction increases as frequency increases.

Fig. 4

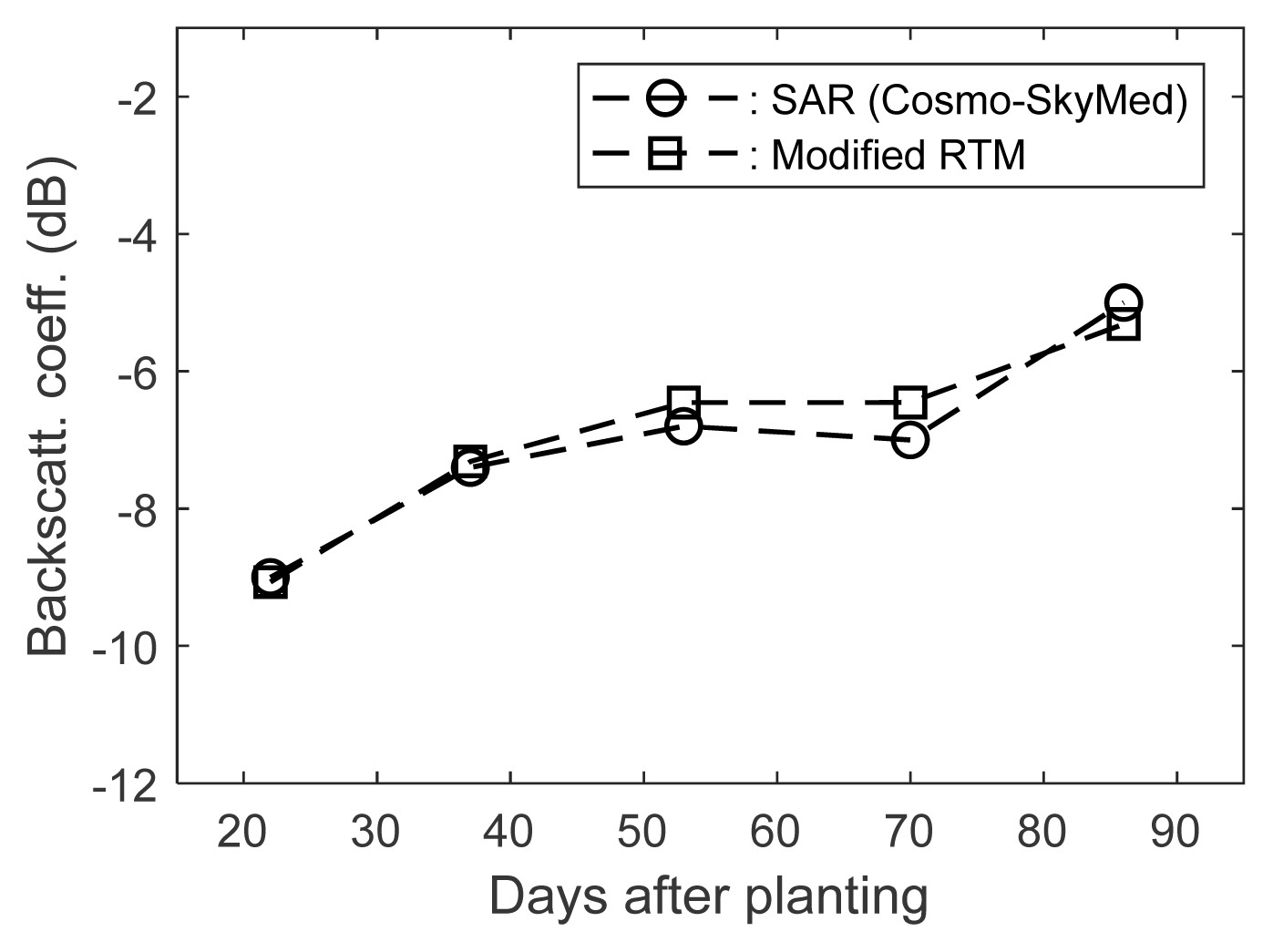
Comparison between COSMO-SkyMed data and modified RTM for a bean field for X-band hh-polarized backscattering coefficients at various days after planting.

There are no changes in the multiple and rough factors: i.e., a multiple factor of 1.0 for hh-polarization and a rough factor of 0.7 for the small-roughness effect.

IV. Concluding Remarks

First, a modified RTM was formulated for estimating the backscattering coefficients of one-layered vegetation fields, and the model was modified on the basis of the HPS measurements and in situ measured ground-truth data for typical agricultural canopies. The modified RTM was multiplied by two multiplicative factors: (1) one is the curvature factor for the curvature effect of leaves and branches (or stems) for all polarizations and (2) the other is the multiple-scattering factor for the cross-polarized backscattering because the cross-polarized backscattering coefficient is very sensitive to the higher-order multiple scattering. In addition to the aforementioned two multiplicative parameters, the small-roughness parameter for microwave reflection from the underlying soil surface was also introduced.

Acknowledgments

The authors would like to thank J. H. Hwang of Seoul National University and S. K. Kweon and S. M. Park of LIGNex1 Co. for providing their valuable measurement data. The authors also thank the anonymous reviewers for their thoughtful comments. This work was supported by the NRF of Korea (2016R1D1A1A09918412).

References

1. Tsang L, Kong JA, Shin RT. Theory of Microwave Remote Sensing 1st edth ed. Hoboken, NJ: Wiley; 1985.

2. Ulaby FT, Long DG. Microwave Radar and Radiometric Remote Sensing Norwood, MA: Artech House; 2014.

3. Ulaby FT, Sarabandi K, McDonald K, Whit M, Dobson MC. Michigan microwave canopy scattering model. International Journal of Remote Sensing 11(7):1223–1253. 1990;

4. Oh Y, Hong SY, Kim Y, Hong JY, Kim YH. Polarimetric backscattering coefficients of flooded rice fields at L- and C- bands: measurements, modeling, data analysis. IEEE Transactions on Geoscience and Remote Sensing 47(8):2714–2721. 2009;

5. Ulaby FT, Elachi C. Radar Polarimetry for Geoscience Applications Norwood, MA: Artech House; 1990.

6. Sarabandi K, Senior TB, Ulaby FT. Effect of curvature on the backscattering from a leaf. Journal of Electromagnetic Waves and Applications 2(7):653–670. 1988;

7. Chang JG, Shoshany M, Oh Y. Polarimetric radar vegetation index for biomass estimation in desert fringe ecosystems. IEEE Transactions on Geoscience and Remote Sensing 56(12):7012–7018. 2018;

8. Oh Y, Jang YM, Sarabandi K. Full-wave analysis of microwave scattering from short vegetation: an investigation on the effect of multiple scattering. IEEE Transactions on Geoscience and Remote Sensing 40(11):2522–2526. 2002;

9. Fung AK, Li Z, Chen KS. Backscattering from a randomly rough dielectric surface. IEEE Transactions on Geoscience and Remote Sensing 30(2):356–369. 1992;

10. Oh Y, Sarabandi K, Ulaby FT. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Transactions on Geoscience and Remote Sensing 30(2):370–381. 1992;

11. Stiles JM, Sarabandi K. Electromagnetic scattering from grassland–Part I: a fully phase-coherent scattering model. IEEE Transactions on Geoscience and Remote Sensing 38(1):339–348. 2000;

12. Stiles JM, Sarabandi K, Ulaby FT. Electromagnetic scattering from grassland–Part II: measurement and modeling results. IEEE Transactions on Geoscience and Remote Sensing 38(1):349–356. 2000;

13. Oh Y, Kay YC. Condition for precise measurement of soil surface roughness. IEEE Transactions on Geoscience and Remote Sensing 36(2):691–695. 1998;

14. Oh Y, Hong JY. Effect of surface profile length on the backscattering coefficients of bare surfaces. IEEE Transactions on Geoscience and Remote Sensing 45(3):632–638. 2007;

15. Sarabandi K, Oh Y, Ulaby FT. Measurement and calibration of differential Mueller matrix of distributed targets. IEEE Transactions on Antennas and Propagation 40(12):1524–1532. 1992;

Biography

Yisok Oh received his B.E. degree from Yonsei University, Seoul, Korea, in 1982, and his Ph.D. degree from the University of Michigan, Ann Arbor, MI, USA, in 1993, all in electrical engineering. In 1994, he joined the faculty of Hongik University, Seoul, where he is currently a professor at the School of Electronic and Electrical Engineering. His current research interests include polarimetric radar backscattering from various Earth surfaces and microwave remote sensing of soil moisture and surface roughness.

Jisung Geba Chang received his Ph.D. degree in geo-information from the Technion – Israel Institute of Technology in 2017. His research area is remote sensing of the environment using multi-temporal data, multi/hyperspectral data, and multi-frequency/polarization SAR data. His current research interest includes machine-learning-based integration of multi-source for classification/clustering and their decomposition.

Maxim Shoshany holds a Ph.D. degree in remote sensing from the University of Tasmania, Australia, in 1990. He is currently a full professor at the Faculty of Civil and Environmental Engineering at the Technion – Israel Institute of Technology. His research area is environmental geo-information, specializing in remote sensing and spatio-temporal modeling of Mediterranean and arid environments.

Article information Continued

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

	RMS deviation (dB)

	Fig. 2			Fig. 3

	Old	New	Δ	Old	New	Δ
VV	1.94	1.28	0.66	3.72	0.95	2.77
HH	1.01	1.39	−0.38	2.89	0.74	2.15
VH	3.39	1.13	2.26	7.88	2.70	5.18