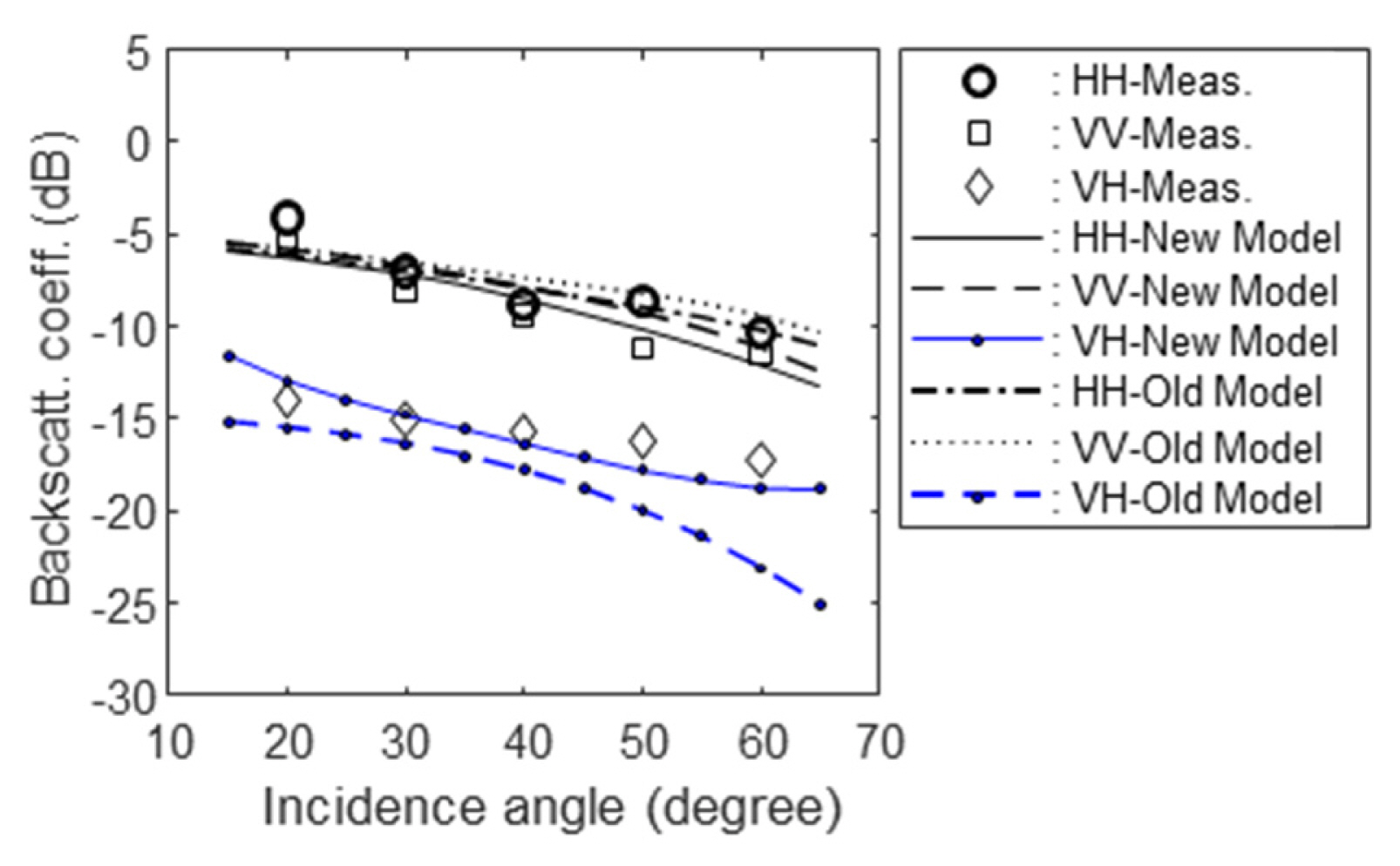
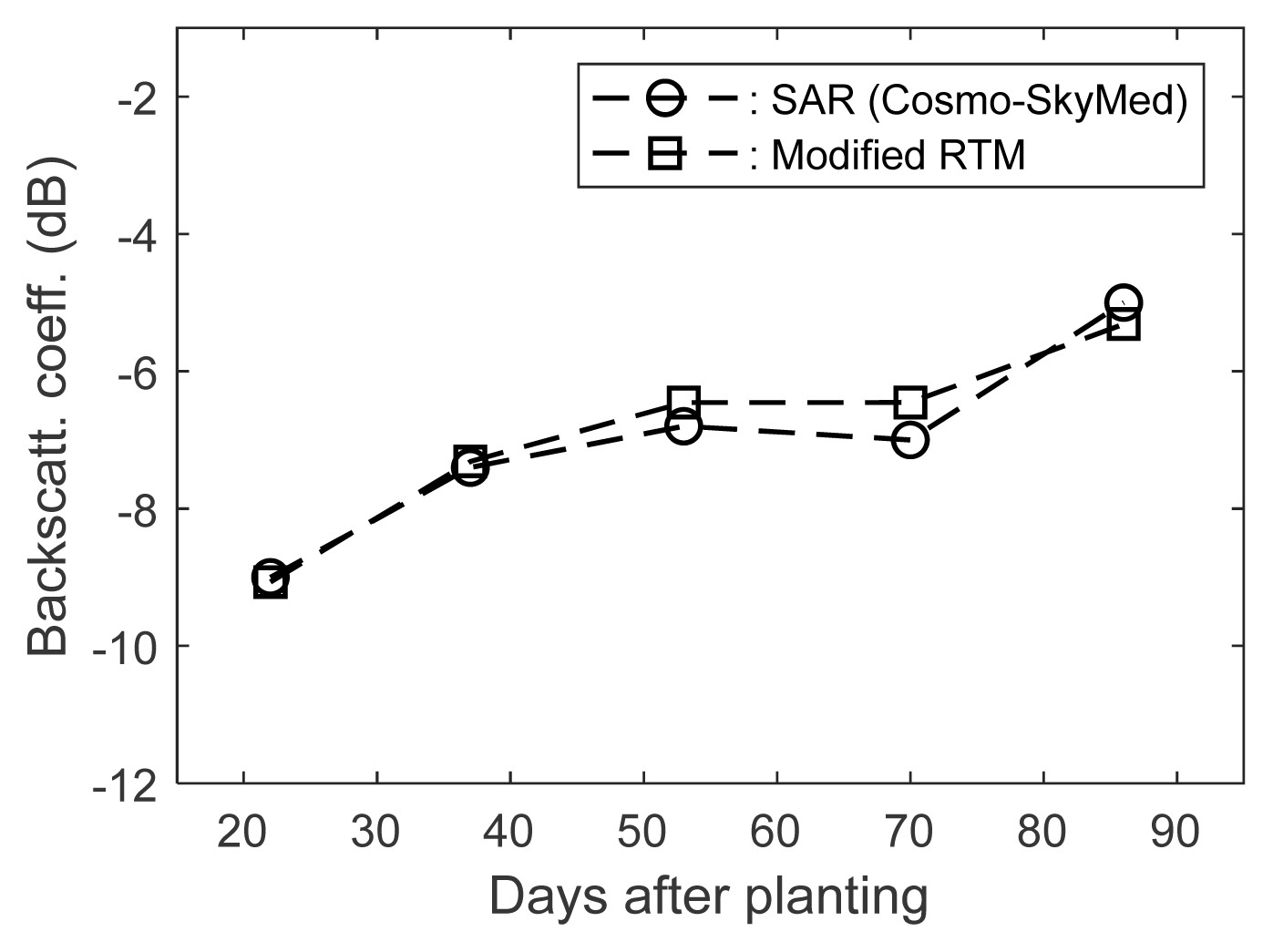
1. L Tsang, JA Kong, and RT Shin, Theory of Microwave Remote Sensing. 1st ed. Hoboken, NJ: Wiley, 1985.
2. FT Ulaby and DG Long, Microwave Radar and Radiometric Remote Sensing. Norwood, MA: Artech House, 2014.
3. FT Ulaby, K Sarabandi, K McDonald, M Whit, and MC Dobson, "Michigan microwave canopy scattering model,"
International Journal of Remote Sensing, vol. 11, no. 7, pp. 1223–1253, 1990.

4. Y Oh, SY Hong, Y Kim, JY Hong, and YH Kim, "Polarimetric backscattering coefficients of flooded rice fields at L- and C- bands: measurements, modeling, data analysis," IEEE Transactions on Geoscience and Remote Sensing, vol. 47, no. 8, pp. 2714–2721, 2009.
5. FT Ulaby and C Elachi, Radar Polarimetry for Geoscience Applications. Norwood, MA: Artech House, 1990.
6. K Sarabandi, TB Senior, and FT Ulaby, "Effect of curvature on the backscattering from a leaf," Journal of Electromagnetic Waves and Applications, vol. 2, no. 7, pp. 653–670, 1988.
7. JG Chang, M Shoshany, and Y Oh, "Polarimetric radar vegetation index for biomass estimation in desert fringe ecosystems,"
IEEE Transactions on Geoscience and Remote Sensing, vol. 56, no. 12, pp. 7012–7018, 2018.

8. Y Oh, YM Jang, and K Sarabandi, "Full-wave analysis of microwave scattering from short vegetation: an investigation on the effect of multiple scattering,"
IEEE Transactions on Geoscience and Remote Sensing, vol. 40, no. 11, pp. 2522–2526, 2002.

9. AK Fung, Z Li, and KS Chen, "Backscattering from a randomly rough dielectric surface,"
IEEE Transactions on Geoscience and Remote Sensing, vol. 30, no. 2, pp. 356–369, 1992.

10. Y Oh, K Sarabandi, and FT Ulaby, "An empirical model and an inversion technique for radar scattering from bare soil surfaces,"
IEEE Transactions on Geoscience and Remote Sensing, vol. 30, no. 2, pp. 370–381, 1992.

11. JM Stiles and K Sarabandi, "Electromagnetic scattering from grassland–Part I: a fully phase-coherent scattering model,"
IEEE Transactions on Geoscience and Remote Sensing, vol. 38, no. 1, pp. 339–348, 2000.

12. JM Stiles, K Sarabandi, and FT Ulaby, "Electromagnetic scattering from grassland–Part II: measurement and modeling results,"
IEEE Transactions on Geoscience and Remote Sensing, vol. 38, no. 1, pp. 349–356, 2000.

13. Y Oh and YC Kay, "Condition for precise measurement of soil surface roughness,"
IEEE Transactions on Geoscience and Remote Sensing, vol. 36, no. 2, pp. 691–695, 1998.

14. Y Oh and JY Hong, "Effect of surface profile length on the backscattering coefficients of bare surfaces,"
IEEE Transactions on Geoscience and Remote Sensing, vol. 45, no. 3, pp. 632–638, 2007.

15. K Sarabandi, Y Oh, and FT Ulaby, "Measurement and calibration of differential Mueller matrix of distributed targets,"
IEEE Transactions on Antennas and Propagation, vol. 40, no. 12, pp. 1524–1532, 1992.