|
 |
- Search
| J. Electromagn. Eng. Sci > Volume 24(2); 2024 > Article |
|
Abstract
This paper presents a novel method for removing noise from range-Doppler images by using a filter prior to conducting target classification using a deep neural network. Specifically, Kuan, Frost, and Lee filters are employed to eliminate speckle noise components from radar data images. Furthermore, a neural network that combines residual and inception blocks (RINet) is proposed. The RINet model is trained and tested on the RAD-DAR dataset—a collection of range-Doppler feature maps. The analysis results show that the application of a Lee filter with a window size of 7 in the RAD-DAR dataset demonstrates the most improvement in the model’s classification performance. On applying this noise filter to the dataset, the RINet model successfully classified radar targets, exhibiting a 4.51% increase in accuracy and a 14.07% decrease in loss compared to the classification results achieved for the original data. Furthermore, a comparison of the RINet model with the noise filtering solution with five other networks was conducted, the results of which show that the proposed model significantly outperforms the others.
Enhancing radar target classification performance using neural networks is a crucial task that researchers worldwide are striving to accomplish. A high-performing neural network model should be characterized by high classification accuracy, low computation time, and a low number of model parameters. Typically, scientists and researchers have employed various approaches to improve the radar target classification performance of neural network models, including feature extraction using preprocessing techniques [1–3], optimization of neural network structures [4, 5], hyperparameter optimization for network training [6], and application of data augmentation algorithms [7].
Notably, radar target classification has unique properties that are distinct from those of camera image classification. First, the signal reflected from radar targets does not display the clear and distinct characteristics of the objects in an image. Second, the noise intensity in radar data is often quite significant, with some cases presenting noise levels that surpass useful signal strength. Therefore, to accurately detect and distinguish targets amid background noise, the application of algorithms, particularly those pertaining to radar signal processing such as accumulation, compression filtering, and noise reduction, is necessary.
In practice, a received signal is susceptible to various types of noise—thermal noise, interference, and clutter [8]. Thermal noise, for instance, is generated by the received signal across the frequency band and the bandwidth of the radar. The other components of a radar, such as the antenna, mixer, and cables, may also contribute to such noise. Notably, thermal noise can be determined using the following equation:
where k is Boltzman’s constant, Bn refers to the frequency bandwidth, and TS indicates the system noise temperature (°K).
In radar systems, waves emitted by active sensors travel in phases, interacting only minimally on their journey to the target area. However, after interacting with the target area, these waves no longer remain in phase due to the different distances they travel from the target which leads to single/multiple bounce scattering. These factors, coupled with signals reflected from various sources, such as the ground, sea, rain, animals/insects, chaff, and atmospheric turbulence, cause interference and clutter noise.
The noise components mentioned above, which appear as light and dark pixels on radar data images, are commonly referred to as speckle noise. This type of noise can be mitigated by employing either multi-look processing or spatial filtering techniques [8]. Notably, multi-look processing is typically performed during the data acquisition stage, whereas speckle reduction through spatial filtering is conducted on the acquired image. Moreover, the spatial filter is generally categorized into two groups: non-adaptive and adaptive. The non-adaptive filter considers the parameters of the entire image signal, disregarding the local properties of the terrain backscatter or the sensor’s nature. As a result, these types of filters are unsuitable for non-stationary scene signals. One example of such filters is the fast Fourier transform technique. On the contrary, an adaptive filter accounts for changes in the local properties of the terrain backscatter and the sensor’s nature. In such filters, the speckle noise is considered stationary, and changes in the mean backscatters caused by different kinds of target are also factored in. An adaptive filter effectively reduces speckles while preserving the edges, thus clearly displaying the unique characteristics of each target. This is a particularly important feature for neural networks used in target recognition. Drawing on the above discussion, this study implemented adaptive filters, such as the Lee [9], Frost [10], and Kuan [11] filters, to reduce speckle noise in data images before feeding them into a neural network for target classification.
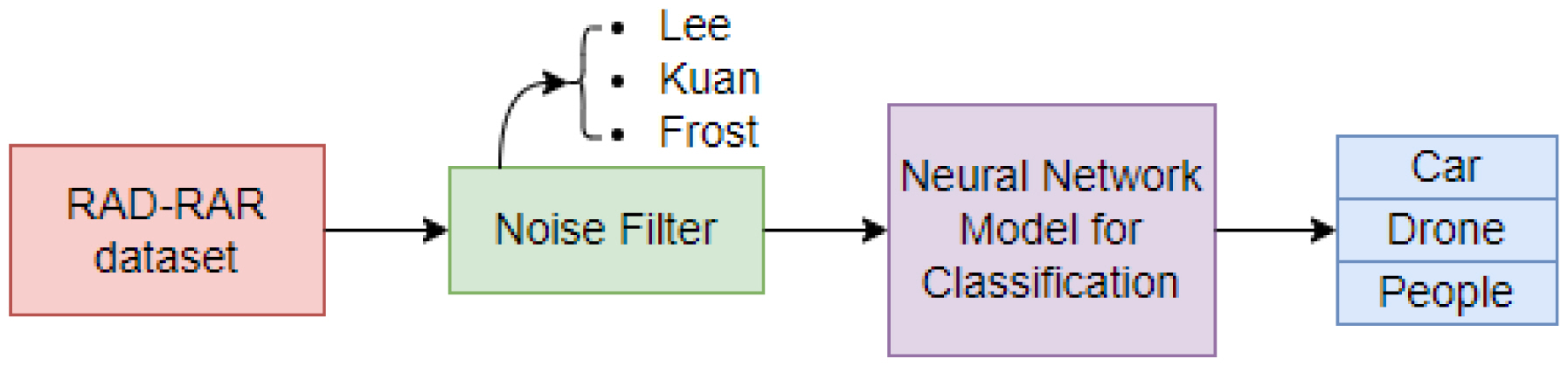
Specifically, this study proposes a residual-inception neural network (RINet) for target classification using range-Doppler radar image data. This involved applying a speckle noise filter to the radar data prior to using it for training and testing the neural network, the experimental process for which is illustrated in Fig. 1. The filter helped reduce speckle noise in the radar dataset by smoothing out the noise while retaining the edges or the sharp features in the image. The experimental results obtained using the preprocessed dataset indicate that the proposed approach can improve radar target classification accuracy by up to 4.51% and decrease loss by 14.07% compared to the classification results obtained using the original data.
The rest of this paper is organized as follows: Section II presents the Real Doppler RAD-DAR dataset and the experimental setup employed to train and test the RINet model, Section III introduces the RINet model used for radar recognition based on range-Doppler feature maps and noise filtering algorithms, Section IV details the experimental results, and Section V provides the concluding remarks.
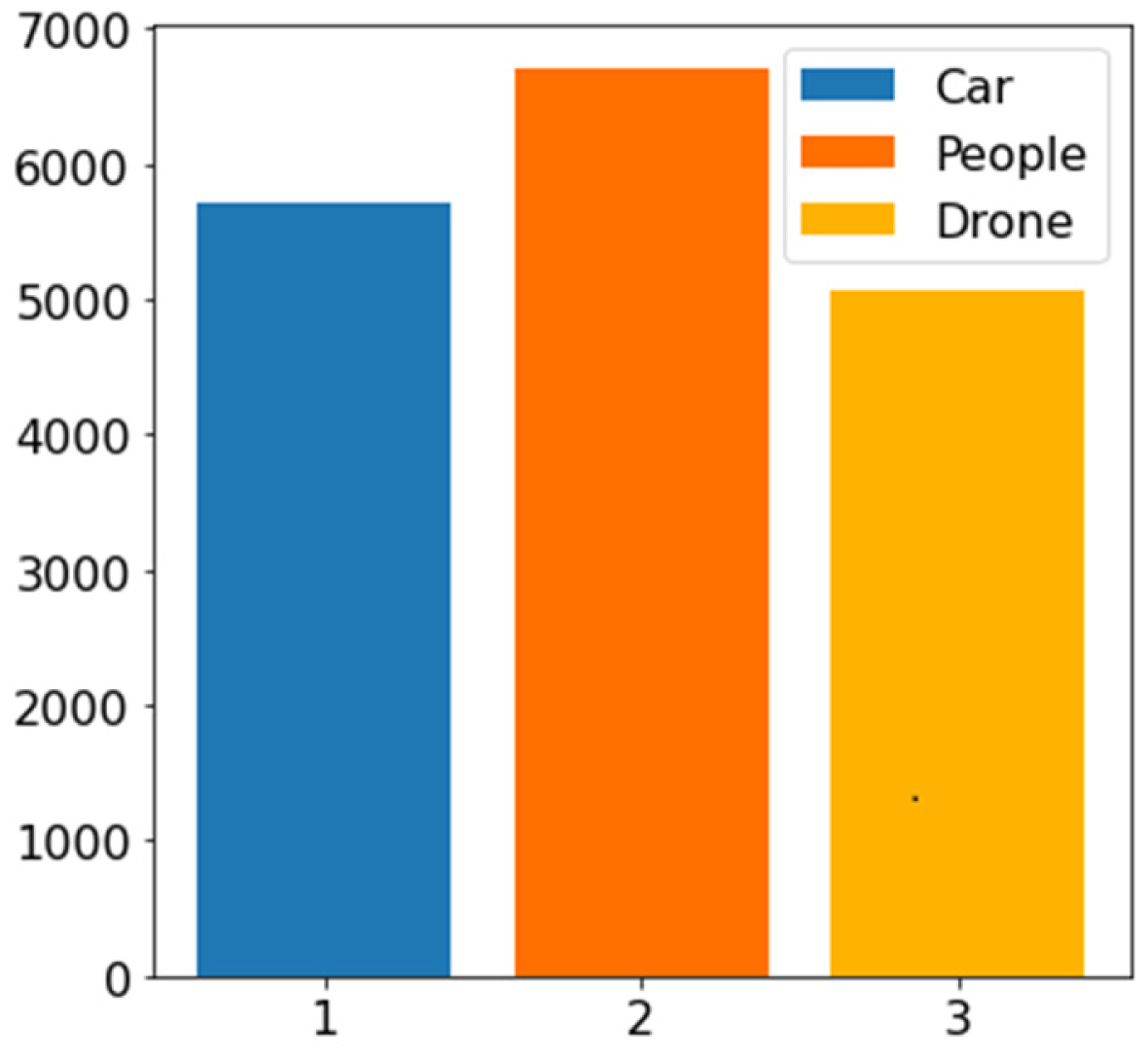
This study utilized the RAD-DAR dataset, collected using an X-band radar system equipped with a digital array receiver, to conduct its analyses. The system employed a frequency-modulated continuous wave with a maximum bandwidth of 500 MHz [4]. The RAD-DAR dataset contains 17,485 data images in the range-Doppler domain annotated with three types of targets: pedestrians, cars, and drones. The sample data for each target were saved in a CSV file with dimensions of 11 × 61 pixels, with 11 pixels corresponding to the range axis and 61 pixels corresponding to the Doppler frequency axis, as illustrated in Fig. 2. The value of each pixel represents the power of the received signal at the corresponding data cell, measured in dBm. The reflected signal strength of the targets in the RAD-DAR dataset was within the range of −140 dBm to −70 dBm. Furthermore, this dataset comprises a balanced distribution of the three target classes, with 38.32% pedestrian samples, 32.71% car samples, and 28.97% drone samples, as shown in Fig. 3.
The RINet model was trained on the RAD-DAR dataset, with 80% of the data for training and 20% for testing. The other predefined training options were a mini-batch size of 32 and an initial learning rate of 0.001. To prevent overfitting, the early-stop algorithm was applied to terminate the training process in the case of no observable improvement in the model’s accuracy for the test set after five training epochs. The RINet model was built using Python programming language and the TensorFlow framework, following which it was trained and tested on a computer with the following configurations: Intel Xeon E5-2678 v3 CPU, RTX 3060 GPU video card, and 32 GB RAM.
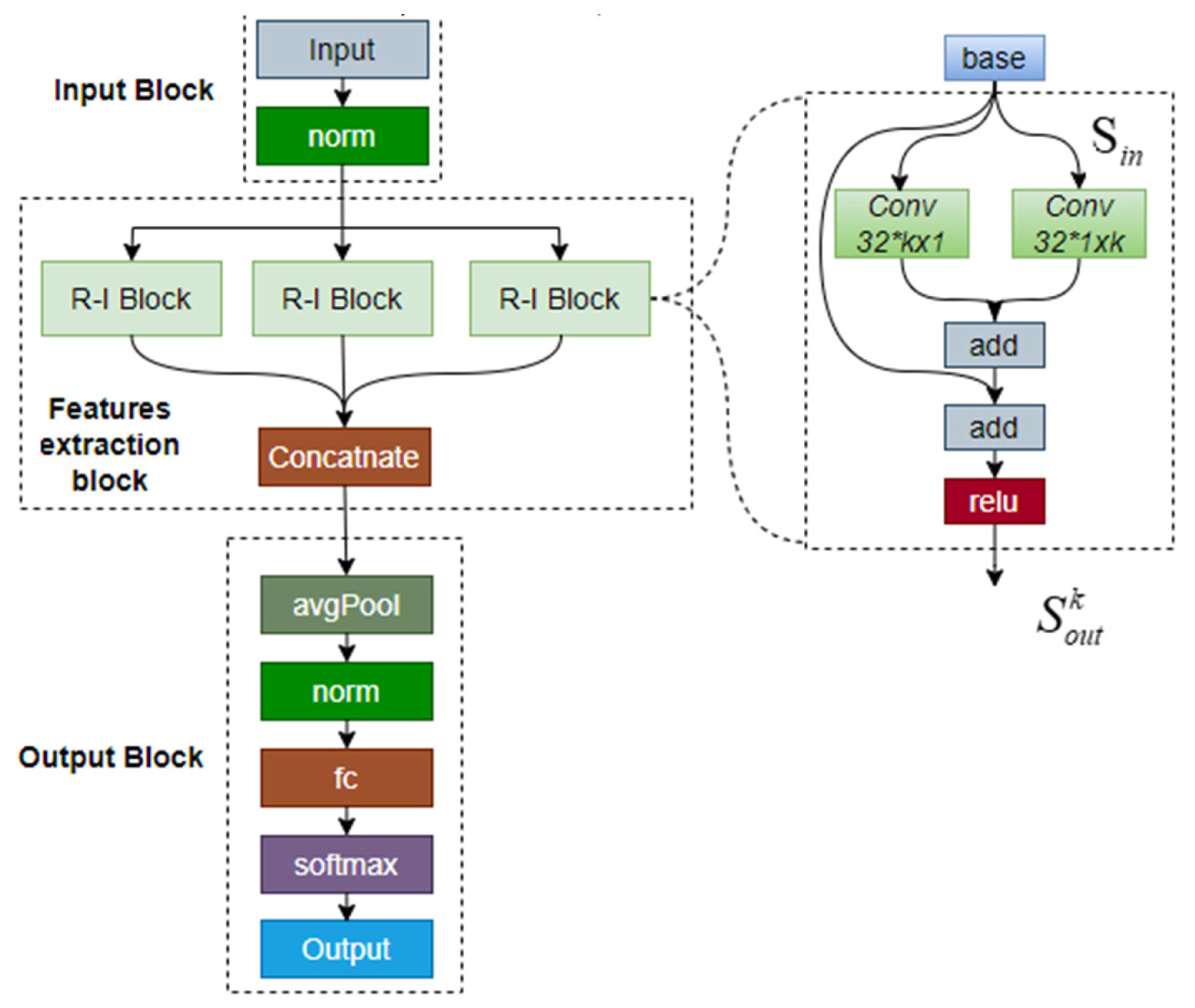
A convolutional neural network (CNN) is a popular algorithm utilized for carrying out deep learning through images and videos. The CNN considered in this study was designed to possess a residual-inception architecture, as shown in Fig. 4. The proposed RINet model comprises three main blocks: input, residual-inception, and output blocks. Furthermore, the feature extraction layer of the model consists of three parallel R-I blocks, each combining inception and residual structures. Each R-I block possesses an inception submodule and its skip connection. The inception module in each R-I block further comprise two parallel convolutional layers, each with 32 filters of size 1×k and k×1, respectively. This design facilitated the reduction of network trainable parameters. The filter size (k) in the three R-I blocks of the RINet model was set to 3, 5, and 7, respectively.
The rectified linear unit (ReLU) activation function was implemented to activate the output of each R-I block. By feeding the input signal Sin to the network’s input layer, the output of the R-I block was obtained using the following equation:
where Fk×1 denotes the convolution operation for the filter of size k×1, and δ denotes the ReLU activation. The output of the concatenation layer was expressed as a tensor combining the feature maps from the previous layer, as follows:
Subsequently, the output feature maps of the three convolutional branches were concatenated in the concatenation layer before being transferred to the output block for target classification. At the output block, average pooling and normalization were performed before feeding to the dense layer, which used the softmax activation function. The output size of the dense layer was three, corresponding to the three types of targets that the model needed to classify. Furthermore, the RINet model employed parallel convolution blocks similar to the inception structure and utilized filters of different sizes in each branch to enhance its feature extraction ability from the input images. The model also reduced the number of trainable parameters by utilizing filters of sizes 1×k and k×1 instead of k×k. Additionally, the RINet model avoided the problems of vanishing gradient and overfitting by employing residual connections.
As mentioned earlier, speckle filtering using adaptive filters involves moving a kernel over each pixel in the image and applying a mathematical calculation using the pixel values under the kernel, after which the central pixel is replaced with the calculated value. The kernel is then moved along the image, one pixel at a time, until the entire image is covered. This process creates a smoothing effect and reduces the visual appearance of the speckle. To examine this function, this paper built three filters—Lee [9], Frost [10], and Kuan [11]—with demonstrated speckle filtering capabilities [12] to filter the noise in the radar images.
The Lee filter reduces speckle noise in images by applying a spatial filter to each pixel. This filter first calculates the local statistics within a square window and then replaces the value of the center pixel with a value calculated using neighboring pixels. The algorithm for the Lee filter involves several steps: 1) calculating the local mean and variance of each pixel using a square window, 2) calculating the signal-to-noise ratio (SNR) for each pixel, 3) calculating the weight of each pixel using the local mean and SNR, and 4) applying the weight to the neighboring pixels to obtain the filtered value for the center pixel. Notably, the Lee filter is well known for its ability to preserve image details while also reducing speckle noise. The above steps of the Lee filter can be described by the following equation:
where K denotes the weight function, PC represents the center pixel value of the window, and LM refers to the local mean of the filter window. Furthermore,
where var(x) is the local variance of the filter window, zm represents the local mean, and
σ n 2
The Frost filter reduces speckle noise while preserving the key image features present at the edges using an exponentially damped circularly symmetric filter that leverages the local statistics within individual filter windows. Its implementation involves defining a circularly symmetric filter with a set of weighting values M for each pixel. The algorithm used in the Frost filter is as follows:
where B=D*(LV/LM*LM) is the weighting factor, S indicates the absolute value of the pixel distance from the center pixel to its neighbors in the filter window, D refers to the exponential damping factor (input parameter), LM is the local mean of the filter window, and LV represents the local variance of the filter window.
The Kuan filter follows a similar process as the Lee filter—reducing speckle noise by applying a spatial filter to each pixel in an image. It filters the data based on the local statistics of the central pixel value, which are calculated using neighboring pixels. Notably, the local statistics are computed using the same expressions as in the Lee filter in (4), with the exact expression for variable K being:
Fig. 5 illustrates the effects of applying the Lee, Kuan, and Frost filters, with a window size parameter of 3, on the range-Doppler map. The filtered output data displays a significant reduction in speckle noise intensity when compared to the original data. Notably, the Kuan filter yields a clearer representation of the target data in the range-Doppler image compared to the Lee and Frost filters. Furthermore, while the output data from the Kuan and Lee filters share a relatively high degree of similarity, both exhibit blurred edges. In contrast, the edges are well preserved in the output image of the Frost filter, although it is worth noting that it contains larger residual noise components compared to the Lee and Kuan filters.
This study evaluated the performance of the RINet model in classifying radar targets by employing four different datasets, including an original dataset and three datasets filtered using Lee, Kuan, and Frost filters bearing a 3 × 3 window size. Specifically, the model was evaluated in terms of classification accuracy and loss. The neural network model exhibited a significant enhancement in its target classification capabilities by utilizing input data noise filters, which effectively eliminated speckle noises. This enabled the neural network to concentrate solely on extracting features from the image regions carrying crucial information about the target. Upon applying the Lee and Kuan filters, the model’s classification accuracy remained comparable, attaining values of 98.17% and 98.06%, respectively. However, the model achieved the highest accuracy (98.17%) and the lowest loss (4.08%) for the dataset filtered by the Lee filter, as presented in Table 1. This outcome highlights the efficacy of the Lee filter in enhancing target classification accuracy.
The output image of the Kuan filter appeared to be cleaner than that of the Lee filter because the former accounts for both signal correlation and noise, as noted in (7). However, when dealing with data inputs possessing a small SNR (drones), the target pixels of the Kuan filter tended to be blurrier than the output image from the Lee filter, thereby hindering the ability to accurately classify the target.
Meanwhile, the Frost filter’s response was dependent on the coefficient of variation, with a high coefficient of variation indicating that the sharp features in the image would be better preserved. As demonstrated in Fig. 5, the Frost filter’s range-Doppler image output retains more noise areas compared to the Lee and Kuan filter output images. As a result, the target classification results of the RINet model for the dataset after the application of the Frost filter were inferior to those achieved by the other two filters.
The Lee filter’s window size parameter was observed to have a significant impact on the filter output data. Notably, larger filter sizes offer a higher noise suppression ability, but at the cost of a decline in the image features at the edges. Therefore, to identify the appropriate window size for the most suitable filter, experiments were conducted on the datasets by considering different window sizes—3, 5, 7, and 9—of the Lee filter. Table 2 reports the target classification results of the RINet model for these datasets. When comparing the three filters with window sizes 3, 5, and 7, it was found that the larger the window size, the better the target classification results. However, when the window size was increased to 9, not only did the filter cause a decline in the target feature but the neural network model’s target classification ability for the concerned dataset also declined, registering an accuracy of 96.14% and a loss of 10.33%. Therefore, for the RAD-DAR dataset, applying the Lee filter with a window size of 7 produced the best results for the RINet model, with an accuracy of 98.87% and an error of 2.61%.
The training and validation accuracy of the RINet model with regard to the RAD-DAR dataset equipped with a Lee filter of window size 7 are plotted in Fig. 6(a), while the training and validation losses are traced in Fig. 6(b). The accuracy and loss curves show that the model exhibits rapid convergence during the training process. Notably, since both the training and validation losses decreased steadily to reach a point of stability, resulting in a minimal gap between their final loss values, a favorable fit was established.
The confusion matrix depicted in Fig. 7 shows that the proposed RINet model attained the least optimal target classification results for the drone sample, achieving an accuracy of 97.31%. The model performed significantly better with regard to the car and people samples, achieving accuracies of 99% and 99.04%, respectively. In this context, it is worth noting that cars and drones share relatively similar visual features, leading to a higher probability of misclassification between these two types of targets compared to the people sample.
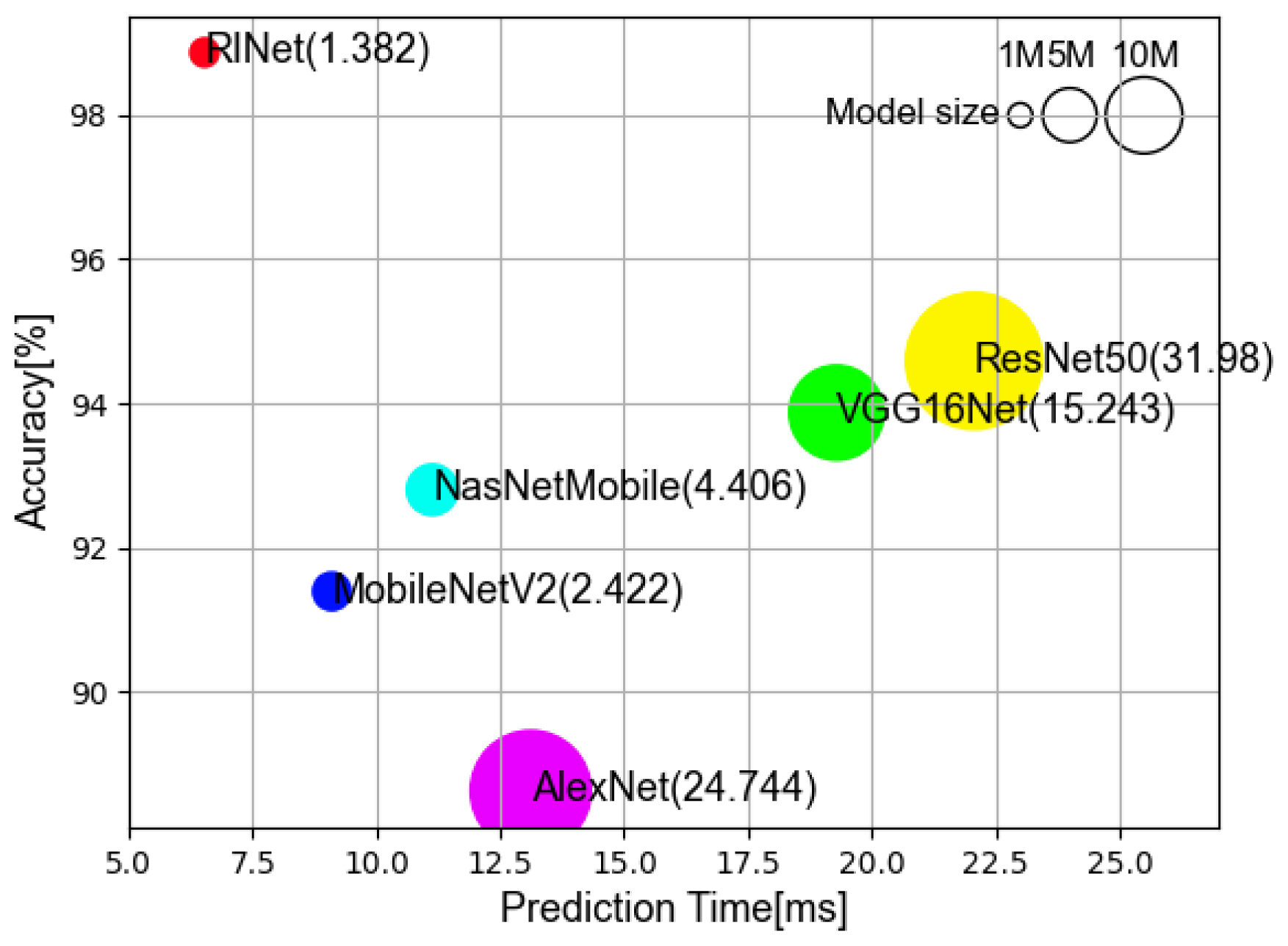
This section compares the classification performance of the proposed RINet model, trained on a dataset preprocessed using a Lee noise filter with a 7 × 7 window size, to those of several other well-known CNN models, namely AlexNet [13], VGG16 [14], ResNet50 [15], MobileNetV2 [16], and NASNetMobile [17], all of which were tested using the original RAD-DAR dataset. The criteria for assessing and contrasting the results were accuracy, prediction time, and model size. Notably, all models were trained using identical parameters to ensure a fair comparison.
The results of the comparison are illustrated in Fig. 8. Among the models tested, AlexNet achieved the lowest accuracy at 88.62%, but exhibited a larger size and prediction time compared to RINet, MobileNetV2, and NasNetMobile. Meanwhile, ResNet emerged as the most accurate model, boasting an impressive accuracy of 94.59%. However, this accuracy was accompanied by a trade-off—the size and prediction time of this model were the largest, amounting to 31.98 million and 22.07 ms, respectively. In contrast, the proposed RINet model demonstrated exceptional performance, was smallest in size, and registered the fastest classification speed, while also maintaining significantly better accuracy than the other models at an impressive 98.87%.
This paper proposes the application of speckle noise filters on the RAD-DAR dataset before conducting target classification using a RINet model that combines inception and residual conceptions to improve radar target classification accuracy. The classification performance of the proposed model, in terms of its accuracy and loss, was evaluated using four datasets. The numerical results showed that the application of data noise filters, such as Kuan, Frost, and Lee filters, helps increase classification performance compared to when only the original data is considered. Moreover, the Lee filter obtained better results than the Kuan and Frost filters. Regarding the impact of the window size of the Lee filter on the RINet model’s classification performance, a higher window size was observed to render more accurate model classification. However, when the filter size was too large, it degraded the target features in the radar data image, leading to a decrease in the model’s target classification accuracy. Therefore, in terms of the RAD-DAR dataset, the RINet model achieved its best radar target classification results when using a Lee filter with a window size of 7. This result was further verified by conducting a performance comparison with five other models: AlexNet, VGG16, ResNet50, MobileNetV2, and NASNetMobile. Drawing on the above-mentioned findings, future research on this topic should continue investigating and applying solutions to improve the probability of correct classification of important targets, such as the drone sample in the dataset considered in this study.
Acknowledgments
This research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 102.04-2021.14.
Fig. 2
Illustration of the gathered frames of the (a) drone, (b) human, and (c) car samples from the RAD-DAR dataset.

Fig. 5
Illustration of frames after applying the filters: (a) original data, (b) Lee filter, (c) Kuan filter, and (d) Frost filter.
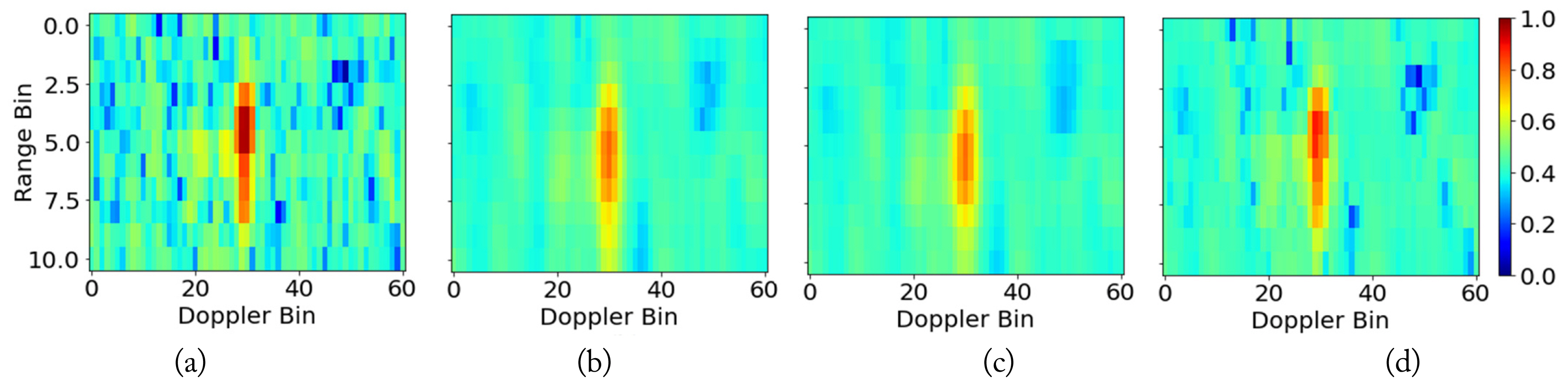
Fig. 6
The model’s target classification results: (a) training and validation accuracies and (b) training and validation losses.

Fig. 8
Comparison of the accuracy, prediction time, and size of the proposed model and other models.
References
1. J. Wan, B. Chen, B. Xu, H. Liu, and L. Jin, "Convolutional neural networks for radar HRRP target recognition and rejection," EURASIP Journal on Advances in Signal Processing, vol. 2019. article no. 5, 2019 https://doi.org/10.1186/s13634-019-0603-y

2. J. Lei and C. Lu, "Target classification based on micro-Doppler signatures," In: Proceedings of IEEE International Radar Conference; Arlington, VA, USA. 2005, pp 179–183. https://doi.org/10.1109/RADAR.2005.1435815

3. S. Lim, S. Lee, J. Yoon, and S. C. Kim, "Phase-based target classification using neural network in automotive radar systems," In: Proceedings of 2019 IEEE Radar Conference (RadarConf); Boston, MA, USA. 2019, pp 1–6. https://doi.org/10.1109/RADAR.2019.8835725

4. I. Roldan, C. R. del-Blanco, A. Duque de Quevedo, F. Ibanez Urzaiz, J. Gismero Menoyo, A. Asensio Lopez, D. Berjon, F. Jaureguizar, and N. Garcia, "DopplerNet: a convolutional neural network for recognising targets in real scenarios using a persistent range–Doppler radar," IET Radar, Sonar & Navigation, vol. 14, no. 4, pp. 593–600, 2020. https://doi.org/10.1049/iet-rsn.2019.0307

5. Y. Kim, I. Alnujaim, S. You, and B. J. Jeong, "Human detection based on time-varying signature on Range-Doppler diagram using deep neural networks," IEEE Geoscience and Remote Sensing Letters, vol. 18, no. 3, pp. 426–430, 2021. https://doi.org/10.1109/LGRS.2020.2980320

6. M. Zhou, B. Li, and J. Wang, "Optimization of hyperparameters in object detection models based on fractal loss function," Fractal and Fractional, vol. 6, no. 12, article no. 706, 2002. https://doi.org/10.3390/fractalfract6120706

7. X. Gao, G. Xing, S. Roy, and H. Liu, "RAMP-CNN: a novel neural network for enhanced automotive radar object recognition," IEEE Sensors Journal, vol. 21, no. 4, pp. 5119–5132, 2021. https://doi.org/10.1109/JSEN.2020.3036047

8. R. K. Raney, "Radar fundamentals: technical perspective," Principals and Applications of Imaging Radar: Manual of Remote Sensing. 3rd ed. New York, NY: John Wiley & Sons, 1998. p.9–130.
9. J. S. Lee, "Digital image enhancement and noise filtering by use of local statistics," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 2, no. 2, pp. 165–168, 1980. https://doi.org/10.1109/TPAMI.1980.4766994


10. V. S. Frost, J. A. Stiles, K. S. Shanmugan, and J. C. Holtzman, "A model for radar images and its application to adaptive digital filtering of multiplicative noise," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 4, no. 2, pp. 157–166, 1982. https://doi.org/10.1109/TPAMI.1982.4767223


11. A. Akl, K. Tabbara, and C. Yaacoub, "An enhanced Kuan filter for suboptimal speckle reduction," In: Proceedings of 2012 2nd International Conference on Advances in Computational Tools for Engineering Applications (ACTEA); Beirut, Lebanon. 2012, pp 91–95. https://doi.org/10.1109/ICTEA.2012.6462911

12. H. Choi and J. Jeong, "Speckle noise reduction technique for SAR images using statistical characteristics of speckle noise and discrete wavelet transform," Remote Sensing, vol. 11, no. 10, article no. 1184, 2019. https://doi.org/10.3390/rs11101184

13. A. Krizhevsky, I. Sutskever, and G. E. Hinton, "ImageNet classification with deep convolutional neural networks," Communications of the ACM, vol. 60, no. 6, pp. 84–90, 2017. https://doi.org/10.1145/3065386

14. K. Simonyan and A. Zisserman, Very deep convolutional networks for large-scale image recognition, 2014. [Online]. Available: https://arxiv.org/abs/1409.1556v1
15. K. He, X. Zhang, S. Ren, and J. Sun, "Deep residual learning for image recognition," In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; Las Vegas, NV, USA. 2016, pp 770–778. https://doi.org/10.1109/CVPR.2016.90

16. M. Sandler, A. Howard, M. Zhu, A. Zhmoginov, and L. C. Chen, "MobileNetV2: inverted residuals and linear bottlenecks," In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; Salt Lake City, UT, USA. 2018, pp 4510–4520. https://doi.org/10.1109/CVPR.2018.00474

17. B. Zoph, V. Vasudevan, J. Shlens, and Q. V. Le, "Learning transferable architectures for scalable image recognition," In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; Salt Lake City, UT, USA. 2018, pp 8697–8710. https://doi.org/10.1109/CVPR.2018.00907

Biography

Van-Tra Nguyen, https://orcid.org/0009-0002-3650-3454 received his M.Sc. degree in electronic engineering from Le Quy Don Technical University in 2016. He is currently pursuing his Ph.D. in radar and navigation technology at the Institute of Radar, Academy of Military Science and Technology, Hanoi, Vietnam. His research interests include radar systems, signal processing, and deep learning techniques.
Biography

Chi-Thanh Vu, https://orcid.org/0009-0008-4047-2877 received his Ph.D. in radar and navigation from Moscow Aviation Institute, Russia, in 2014. He heads the Signal Processing Research Group on Radar at the Institute of Radar, Academy of Military Science and Technology, Hanoi, Vietnam. His research interests include radar and sonar systems, signal processing, and deep learning techniques.
Biography

Van-Sang Doan, https://orcid.org/0000-0001-9048-4341 received his M.Sc. and Ph.D. degrees in electronic systems and devices from the Faculty of Military Technology, University of Defence, Brno, Czech Republic, in 2013 and 2016, respectively. He was awarded Honors degrees by the Faculty of Military Technology of the University of Defence in 2011, 2013, and 2016. From 2019 to 2020, he was a post-doctoral research fellow at the ICT Convergence Research Center, Kumoh National Institute of Technology, South Korea. He is currently a lecturer at the Faculty of Communication and Radar, Naval Academy in Nha Trang City, Vietnam. His current research interests include radar and sonar systems, signal processing, and deep learning.
- TOOLS
- Related articles in JEES