Analysis of Cross-Polarized Field by Panel Misalignment Errors in a Deployable Reflector Antenna

Si-A Lee; Seung-Joo Jo; Suk-Jin Kim; Taek-Kyung Lee; Jae Wook Lee

doi:10.26866/jees.2023.1.r.140

J. Electromagn. Eng. Sci > Volume 23(1); 2023 > Article

Lee, Jo, Kim, Lee, and Lee: Analysis of Cross-Polarized Field by Panel Misalignment Errors in a Deployable Reflector Antenna

Regular Paper

Journal of Electromagnetic Engineering and Science 2023;23(1):18-26.

Published online: January 31, 2023

DOI: https://doi.org/10.26866/jees.2023.1.r.140

Analysis of Cross-Polarized Field by Panel Misalignment Errors in a Deployable Reflector Antenna

Si-A Lee¹, Seung-Joo Jo¹, Suk-Jin Kim², Taek-Kyung Lee^2,^*, Jae Wook Lee²

¹Satellite System Team 1, Hanwha Systems, Yongin, Korea

²School of Electronics and Information Engineering, Korea Aerospace University, Goyang, Korea

^*Corresponding Author: Taek-Kyung Lee (e-mail: tklee@kau.ac.kr)

Received March 11, 2022 Revised July 18, 2022 Accepted November 11, 2022

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

This paper analyzes the generation mechanism of a cross-polarized field resulting from panel misalignment errors in a solid-surface deployable antenna. Misalignment of the panel in a deployable antenna results in path length error and rotation of the unit normal vector on the reflector surface. However, in terms of the analysis of cross-polarization (cross-pol) generation, rotational error is a more significant factor. In the aperture field, the distributions of cross-pol components are calculated to identify the polarization characteristics of the radiated field. For uniform misalignment, the peak-to-cross polarization (XPOL) is found to be smaller than −50 dB for misalignment angles less than 3°. Furthermore, when the panels are non-uniformly misaligned with a sinusoidal distribution, the cross-pol level depends on the angular position of the maximum misalignment.

Keywords: Cross-Pol Generation, Deployable Antenna, Normal Vector Rotation, Panel Misalignment

I. Introduction

Reflector antennas are increasingly being used in small- and medium-sized satellites because they are lightweight and operate over a broad bandwidth. Moreover, deployable reflector antennas can increase the storage efficiency of satellites in launch vehicles. Compared to a mesh reflector antenna, an antenna composed of solid material has higher surface accuracy and possesses the advantage of low cross-polarization (cross-pol) [1, 2]. Recently, the cross-pol characteristics of the antenna have been gaining significance in SAR systems, which can be operated in a polarimetric mode [3, 4]. This is because the cross-polar level in an antenna pattern induces cross-talk in polarimetric SAR images [3].

In a perfect parabolic reflector, cross-polarization is generated by an unbalanced feeder whose feed pattern is rotationally asymmetrical [5]. However, the surface error of the reflector may also generate cross-polarized radiation, even in the case of a balanced feeder. In solid-surface deployable antennas, panels are folded during launch and unfolded during deployment in space [6]. If the antenna is imperfectly deployed in space, the panels are misaligned from the ideal shape [7]. Furthermore, in the case of incomplete deployment, the panels are uniformly misaligned. The panels may also misalign non-uniformly, with the error changing smoothly in the angular direction due to malfunctions in the deployment mechanism. In view of these circumstances, it would be interesting to explore the effects of misalignment error on the radiation pattern of a deployable antenna.

The surface error in a reflector antenna leads to a phase error in the aperture plane due to the path-length difference [8]. For panel misalignment, degradations in co-polarization characteristics are calculated using the aperture phase error (APE) method, which calculates the radiated field from the aperture field by accounting for the phase errors caused by the surface error of the reflector [9]. When the panels are uniformly misaligned, the gain decreases, while the side lobe level also increases with an increase in the error. Apart from this, for an asymmetrical distribution of panel misalignment errors, tilting of the main beam is observed.

Cross-pol in far-field radiation is caused by the cross-pol component in the aperture [5]. However, the APE method does not provide sufficient information when it comes to analyzing cross-pol performances because the cross-polar component is not included in the calculation of the aperture field [8, 9]. When panels are misaligned, the direction of the normal vector on the surface rotates in terms of the misalignment angle, in addition to the path-length difference. In the aperture plane, disturbance of the polarization purity arises from the rotation of the normal vector, as well as from the phase difference. Notably, the rotation of the normal vector is a more important factor in cross-pol generation than the phase difference. Therefore, by investigating the rotational effect of the normal vector on the polarization characteristics in the aperture plane, it is possible to estimate the cross-pol performance of radiation in the far-field region. However, although it is convenient to calculate cross-pol radiation using commercial tools based on numerical methods [10], it is difficult to identify the causes of cross-pol generation resulting from panel misalignments. Therefore, to mitigate cross-pol generation from reflector antennas, a physical understanding of the causes leading to cross-pol occurrence in an aperture is required.

In this paper, the effects of panel misalignment errors on the cross-pol performance of a solid surface deployable antenna are analyzed. To separate the investigation of the influence of the panel error from that of the feeding unbalance, the incident field from the feeder is assumed to be a symmetrical Gaussian beam. The cross-pol performances are analyzed using the aperture cross-pol field (AXPF) method, in which the cross-pol radiation field is calculated from the aperture cross-pol field, which is obtained by counting the effects of the normal vector’s rotation as well as the phase error caused by panel misalignment. In other words, the AXPF method provides a physical interpretation of the mechanism of cross-pol occurrence in the aperture. For some typical types of error distributions, including uniform and cosine shapes, the generation of the cross-pol was analyzed and compared to each other by investigating the aperture field.

II. Cross-Pol Characterization using the Aperture Cross-Pol Field Method

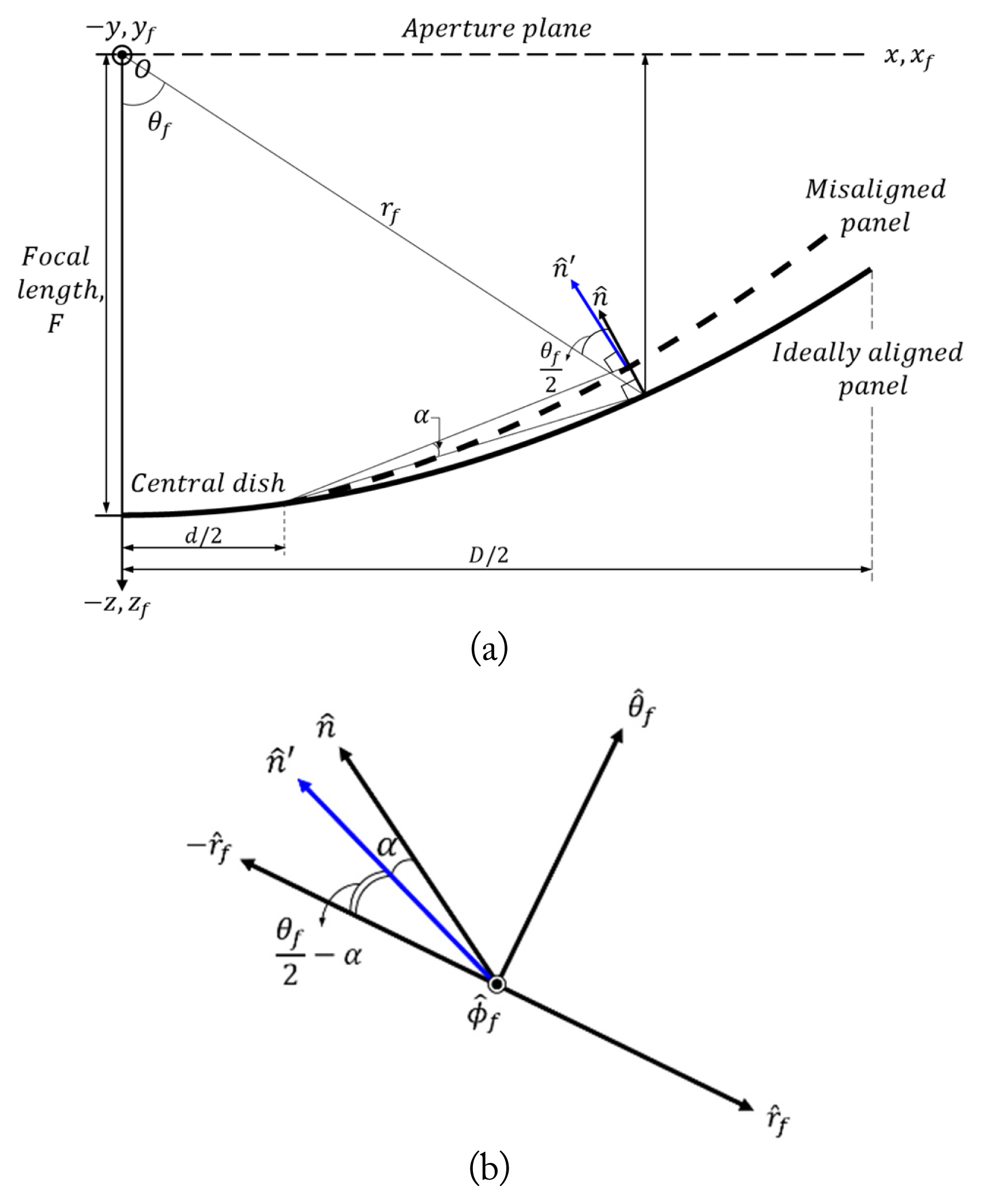
Fig. 1(a) presents the cross-sectional configuration of the reflector of the solid-surface deployable antenna. The reflector consists of a central dish and panels. The diameters of the reflector and the central dish are D and d, respectively. When the panels are completely deployed, the central dish and the panels are assumed to be ideally parabolic with no errors. The feeder is located at the focal point, which is the origin of the coordinates. If the panels are incompletely deployed, the misaligned panel, denoted by a dotted line in Fig. 1(a), is rotated to the misalignment angle α from the ideally aligned panel [9]. The misalignment angle α refers to the angle error of an incompletely deployed panel, which is rotated at the rim of the central dish from the ideal shape, as illustrated in Fig. 1(a). The panel misalignment accompanies the path-length difference from the feeder to the aperture plane, as well as the rotation of the normal vector on the reflector surface. In the AXPF method, the aperture field is calculated by counting the effects of the rotation of the normal vector and the phase error resulting from the path length difference. The unit normal vector of the misaligned panel, denoted by n^', is rotated to angle α from the normal vector n^ of the ideal surface. In the spherical coordinates (r_f,θ_f,φ_f) of the corresponding rectangular coordinates (x_f,y_f,z_f), the n^' for arbitrary φ_f can be expressed, as depicted in Fig. 1(b), as:

(1)

n^′=-r^f cos (θf2-α)+θ^f sin (θf2-α).

To investigate the effects of panel misalignment on cross-pol generation separately from the feeder unbalance, the feeder is assumed to have a balanced pattern in which the E-plane and H-plane patterns are equal. For a balanced feeder with an x-polarized radiation pattern, the incident wave onto the reflector is expressed as [5]:

(2)

Ei=V0e-jkrfrfC(θf)(θ^f cos φf-φ^f sin φf),

where C(θ_f) is the pattern in the E- and H-planes. Furthermore, the reflected wave from the misaligned panel is expressed as E_r =2(n^' · E_i)n^'–E_i [5], using the rotated unit normal vector n^'. For a misaligned panel with a misalignment angle α, the aperture field is given by considering the phase error and the rotated normal vector, which is expressed from the derivation in Appendix A as follows:

(3)

Ea(θf,φf)=V0e-jk2FrfC(θf)(x^ACO+y^ACX+z^AZ)ejδm,

where

(4)

ACO=2 sin2 α cos2 φf-1,ACX=-sin2 α sin 2 φf,AZ=-cos φf sin 2 α.

Here, δ_m indicates the phase error calculated from the path length error at the m-th panel [8, 9]. In the aperture field expressed in (3), A_CO and A_CX are the x- and y-direction components that contribute to the generation of co-polarized and cross-polarized radiation fields, respectively. Meanwhile, A_Z refers to the z-direction component of the aperture field, which does not contribute to the radiation field. The rotation of the normal vector by angle α and phase error δ_m result from the panel misalignment. Moreover, since α is small positive when the panel is incompletely deployed, A_CO exhibits almost unity although A_CX is not negligible for the small α. While the copol radiation degrades mainly due to the phase error δ_m [9], cross-pol generation is seriously affected by the rotation of the normal vector.

From (4), it is understood that the cross-pol does not occur in the aperture field if the panels are completely deployed (α=0 and n^'=n^). For the misaligned panels, the unit normal vector n^' can be decomposed into the normal component in the n-direction and the tangential component in the t-direction on the surface of ideally aligned panels, as shown in Fig. 2. The unit normal vector n^' on the surface of the misaligned panel can therefore be expressed using the unit vectors n^ and t^ as:

(5)

n^′=n^Pn+t^Pt,

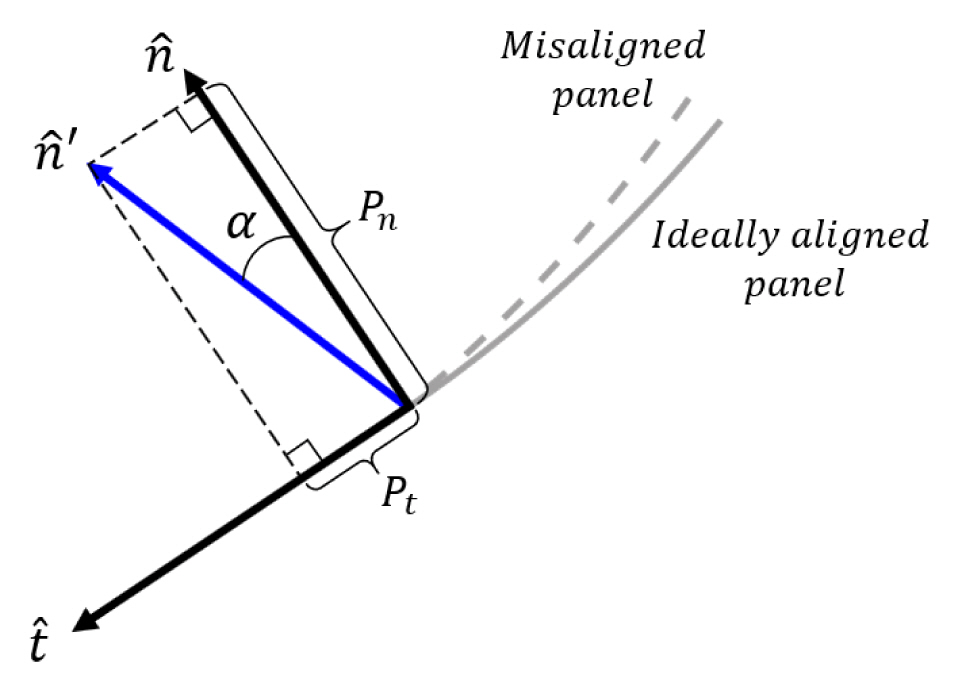
where P_n=cosα and P_t =sinα are the normal and tangential components of n^', respectively. Furthermore, in terms of the geometry in Fig. 1(a), the unit vectors n^ and t^ may also be expressed as:

(6)

n^=-r^f cos θf2+θ^f sin θf2,t^=-r^f sin θf2-θ^f cos θf2

Using (2) as an incident x-polarized field from the feeder and n^ in (5), we can derive the cross-pol component of the aperture field as:

(7)

ACX=Pt2 sin 2 φf.

From (7), it is clear that in the rotated unit normal vector n^' due to the misalignment, the cross-pol field at the aperture is generated from the tangential component P_t, while the normal component P_n is not related to the generation of any cross-pol field. Therefore, to investigate the generation of a cross-pol field, it is necessary to first observe the rotation of the unit normal vector on the surface of the panel that is caused by the misalignment.

III. Effects of Panel Misalignment on Cross-Pol Radiation

The generation of cross-pol fields due to panel misalignments in the deployable antenna utilized in this research is investigated by analyzing the aperture fields. The diameters of the antenna and the central dish are 1.5 m (D) and 0.2 m (d), respectively. Additionally, the operating frequency is fixed at 9.6 GHz, and the focal length is 0.45 m (F). The number of panels is 30. Furthermore, x-polarized balanced feeding is assumed. Additionally, C(θ_f) is defined using a Gaussian function when the edge taper is −12 dB.

1. Uniform Panel Misalignment

This section details the analysis of cross-pol characteristics when the misalignment angle (α) is equal for all panels. Since the radiation field is a Fourier integration of the aperture field in (3), the generation of the cross-pol field can be estimated by investigating the behavior of A_CX. It has been confirmed that the effect of δ_m on cross-pol generation is negligible for small α. Drawing on (7), Pt2 is considered to be a constant for uniform misalignment, with A_CX changing along with sin2φ_f. Fig. 3 shows the distribution of A_CX in the aperture resulting from normal vector rotation when α is 1°. It is observed that A_CX is negative in the 1st and 3rd quadrants, but positive in the 2nd and 4th quadrants. In addition, A_CX is noted to be point symmetric about the center. In addition, the net amount of the cross-pol component in the aperture is found to be zero, since A_CX changes two cycles of the sine function in the φ_f-direction.

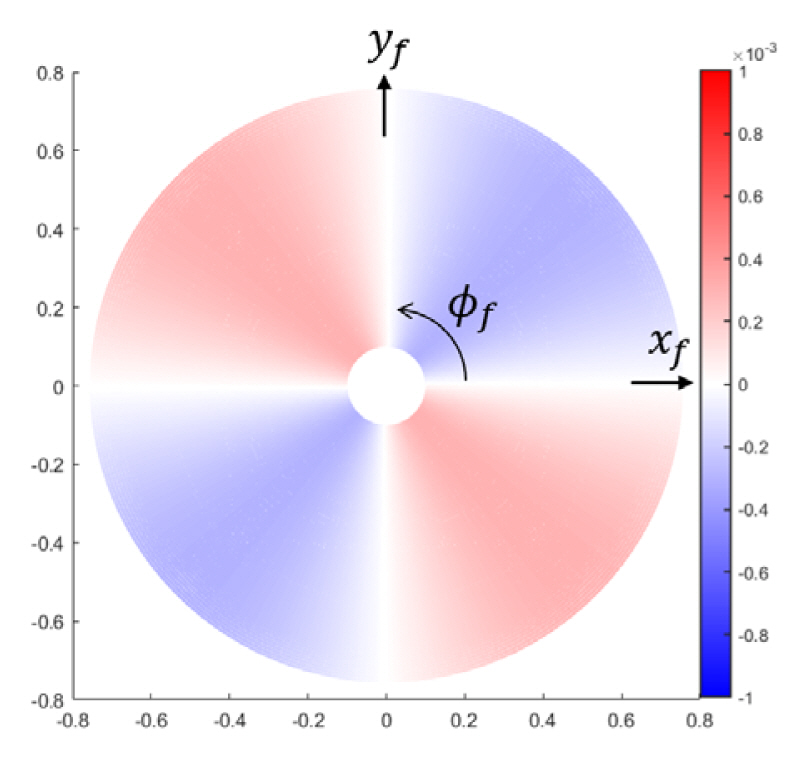
The pattern factor of the radiated field in the far-field region can be obtained from the two-dimensional Fourier integral of (3). This integration is performed numerically by dividing the aperture region into trapezoidal micro-regions using a Gaussian quadrature. In radiated electromagnetic fields, the cross-pol field defined by Ludwig [11] is generated from the y-component of the aperture field. Therefore, the distribution of A_CX, as shown in Fig. 3, is an important feature in terms of dealing with the cross-pol field.

With regard to the E-plane (φ=0 or π) and H-plane ( φ=π2 or 3π2), Fig. 3 indicates that the cross-pol field vanishes, since distances from the positive A_CX and negative A_CX to the observation point are the same, with the corresponding radiated fields canceling each other. In the φ=π4 plane, the radiated cross-pol field exists because A_CX at the same distances from the observation point are equal.

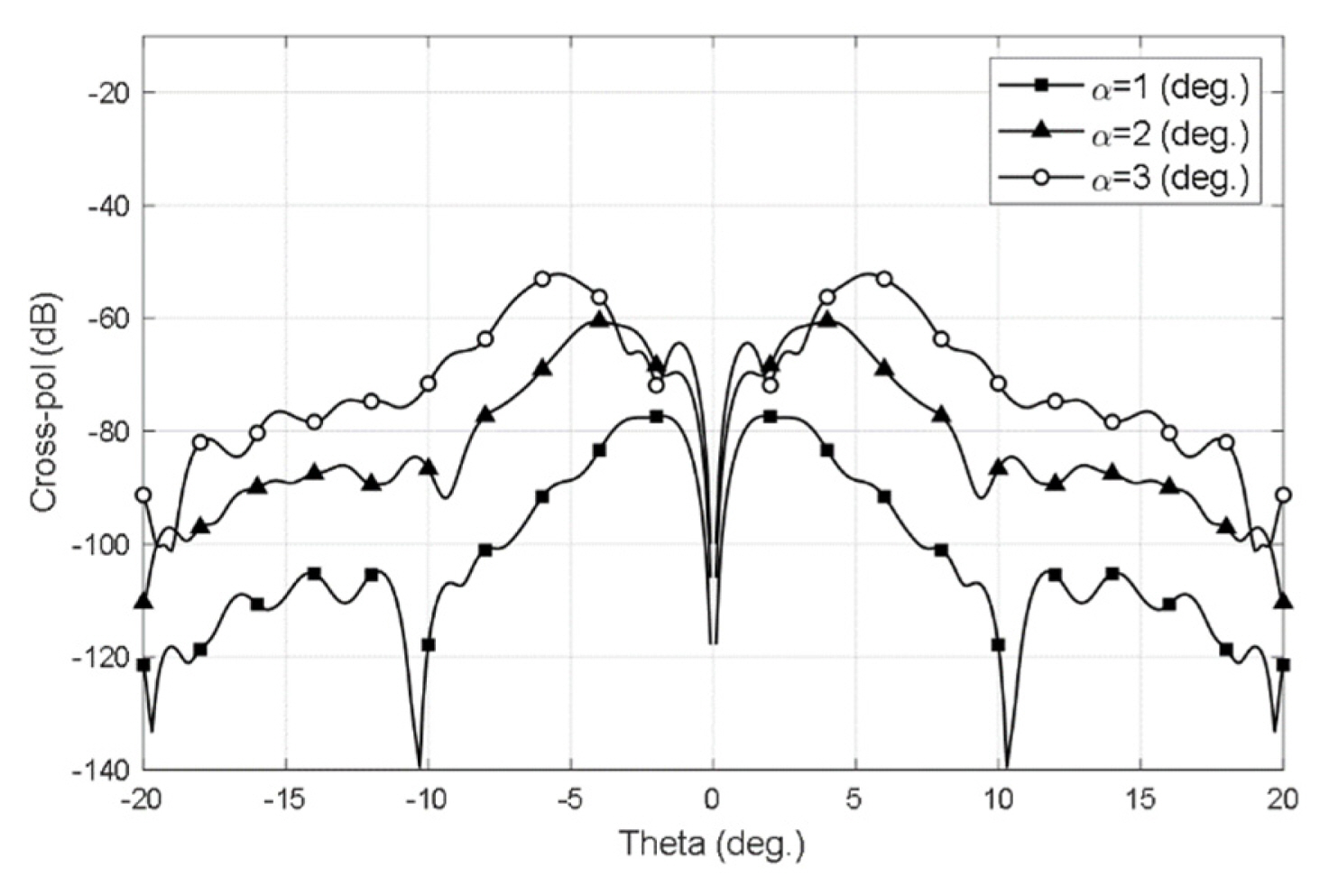
Fig. 4 depicts the cross-pol patterns in the φ=π4 plane for α=1°, 2°, and 3°. It is clear that cross-pol radiation increases along with an increase in the misalignment angle. However, for uniform misalignment error, the peak-to-cross polarization (XPOL) is smaller than −50 dB for a misalignment angle of up to 3°. Moreover, since the distribution of A_CX in the aperture is anti-symmetric about the x- and y-axes and the net amount is zero, the cross-pol radiation is very small. Notably, for co-pol radiation, the gain and pattern degrade significantly due to uniform panel misalignment [9].

2. Non-uniform Panel Misalignments

It would be interesting to investigate the generation of the cross-pol field in cases where the distribution of the panel misalignment error is non-uniform. By investigating aperture cross-pol fields, it is possible to estimate the levels of cross-pol radiation for non-uniform panel misalignments. As a typical model of the non-uniform distribution of misalignment errors, we chose sinusoidal functions. Since misalignment angles resulting from incomplete deployment always have a positive value, we assume the misalignment angle of the k-th panel to be:

(8)

αk=12αm (1+cos N (φk-φαm)),

where k indicates the sequential number of the panel, which increases from the panel at φ=0. Meanwhile, φ_k denotes the angle in the φ-direction at the middle of the k-th panel, α_m indicates the maximum error, and φ_α_{_m} refers to the angle exhibiting the maximum error. Inside the panel, the misalignment angle is assumed to be uniform.

2.1. 1-Cycle Non-uniform Misalignments

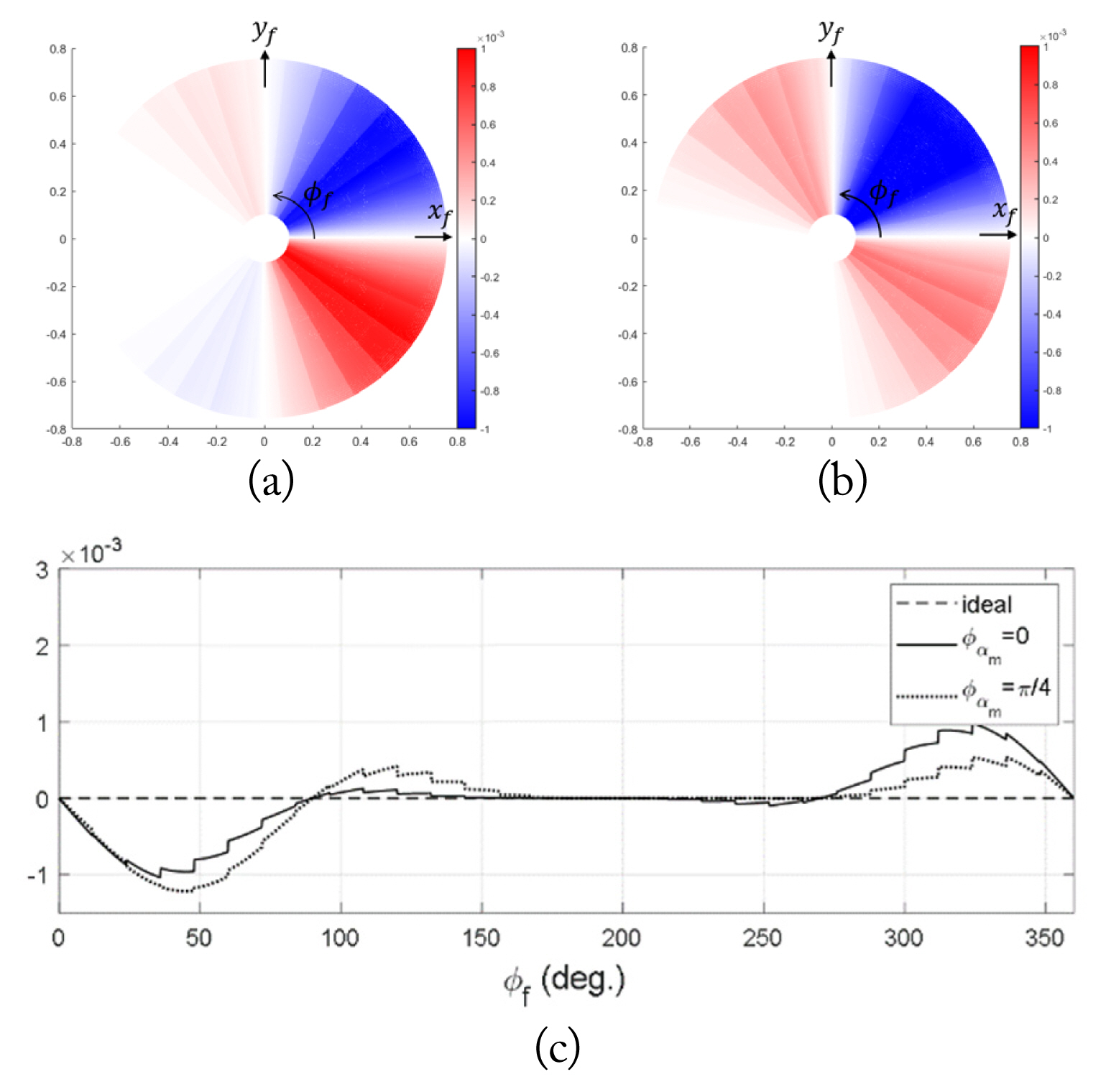
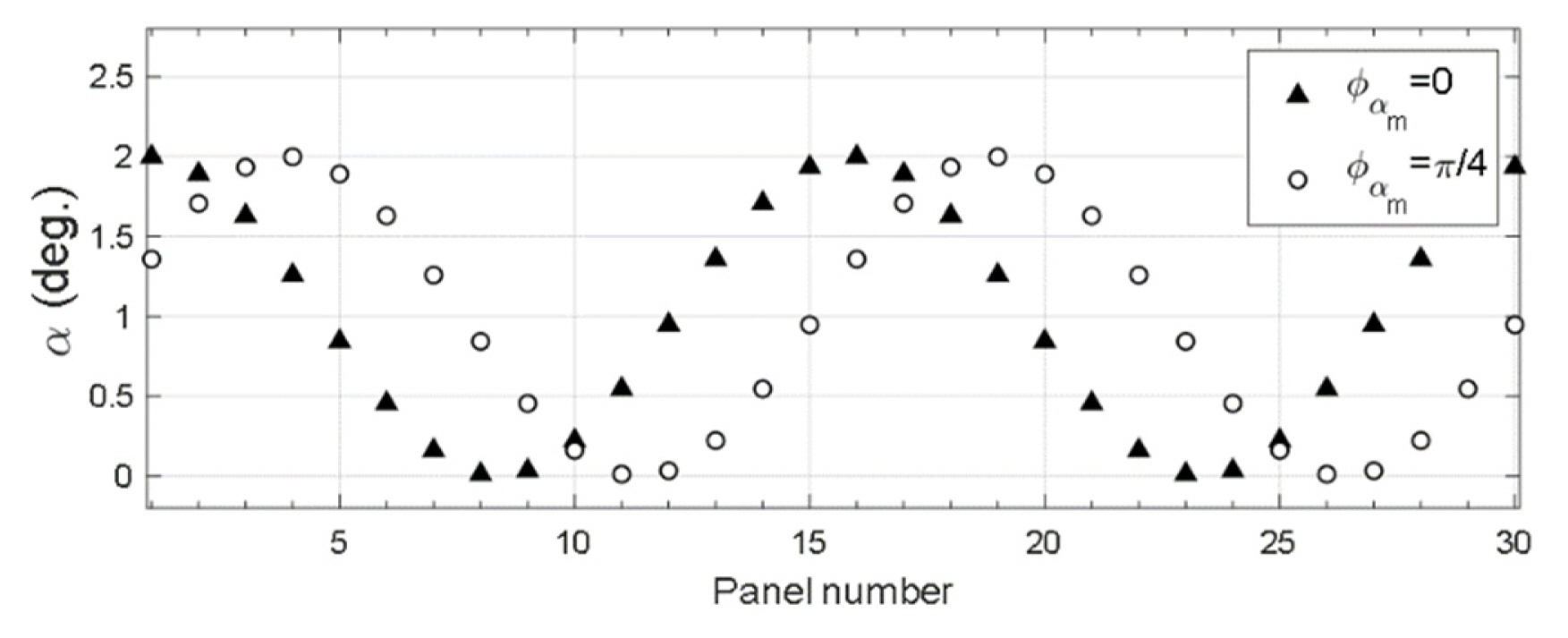
For N = 1, α_k varies one cycle for the change of φ_k from 0 to 2π. Fig. 5 depicts the variations in α_k for the panels when φ_α_{_m}=0 and π4. Here, α_m is 2° so that the average value is 1°. When φ_α_{_m}=0, the misalignment error is maximum at the 1st panel (φ_k =0) and minimum at the 16th panel (φ_k =π). Furthermore, as shown in Fig. 5, the configuration of the error distribution is rotated by φ_α_{_m} in the φ-direction for φαm=π4.

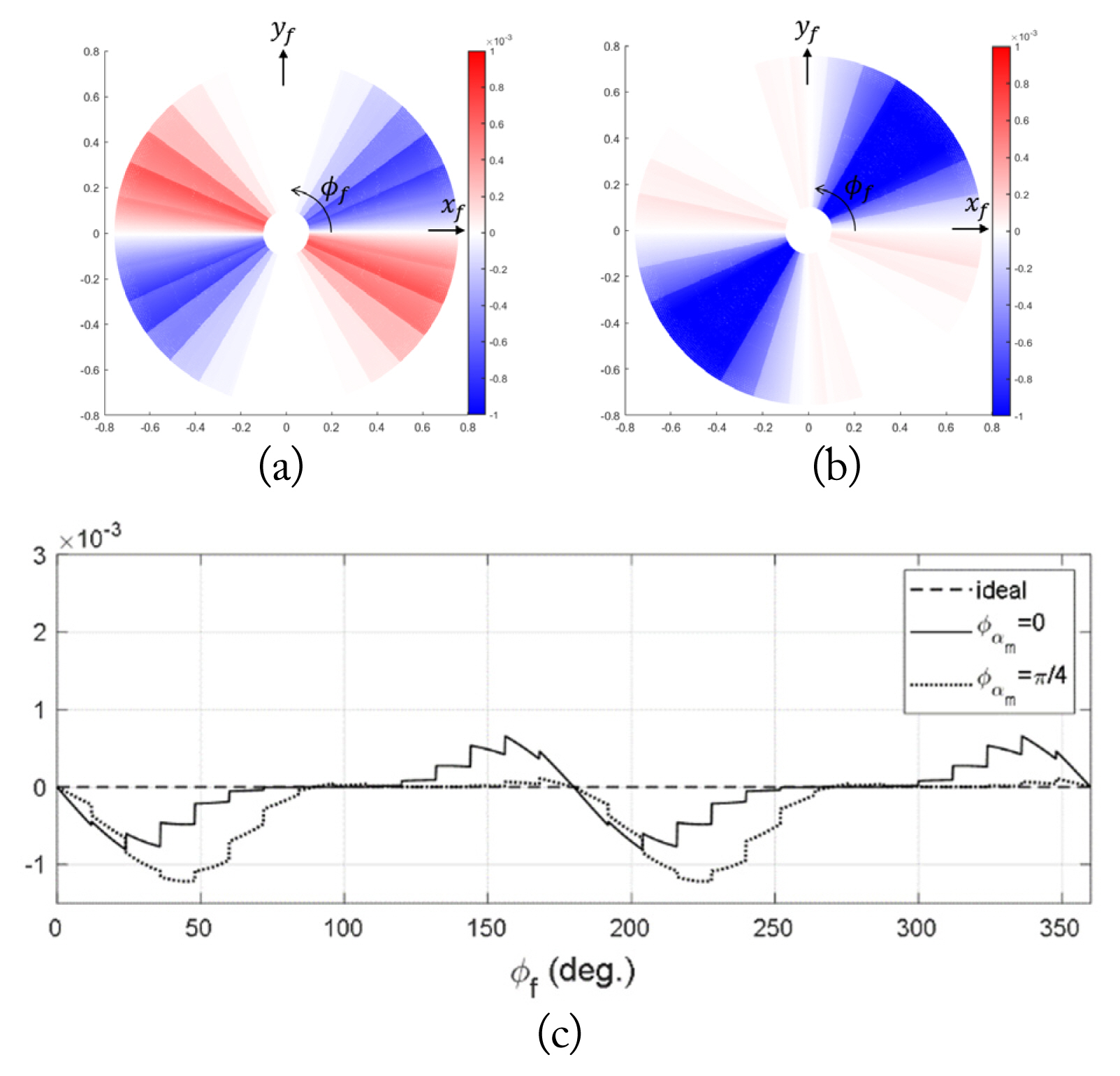
From (7), we note that A_CX is positive in the 1st and 3rd quadrants, while it is negative in the 2nd and 4th quadrants, regardless of whether the misalignments are uniform or not. Fig. 6(a) shows the A_CX distribution for 1-cycle misalignment with φ_α_{_m}=0. Since Pt2=sin2αk, with α_k’s in Fig. 5 for φ_α_{_m}=0, the A_CX about the x-axis is anti-symmetric. Furthermore, since the net amount of A_CX in the aperture vanishes, the cross-pol radiation is expected to be small. When φ_α_{_m} changes from zero, the anti-symmetry of the distribution is not sustained, while the net amount of A_CX does not vanish. In other words, cross-pol radiation increases when φ_α_{_m} changes its value from zero. Fig. 6(b) presents the A_CX distribution for φαm=π4, where the positive quantity in the 2nd quadrant is greater than the negative quantities in the 1st and 3rd quadrants. Fig. 6(c) illustrates the A_CX variations for φ_α_{_m}=0 and π4 in the φ-direction for comparison. Meanwhile, Fig. 7 shows the cross-pol patterns in the φ=π4 plane, where it is confirmed that the cross-pol level is higher for φαm=π4 than for 0.

Since the level of cross-pol radiation depends on the net amount of A_CX in the aperture, the average aperture cross-pol for a balanced feeder pattern may be expressed as:

(9)

FA=12π|∫02πACXdφf|=12π|∫02πPt2 sin 2 φfdφf|,

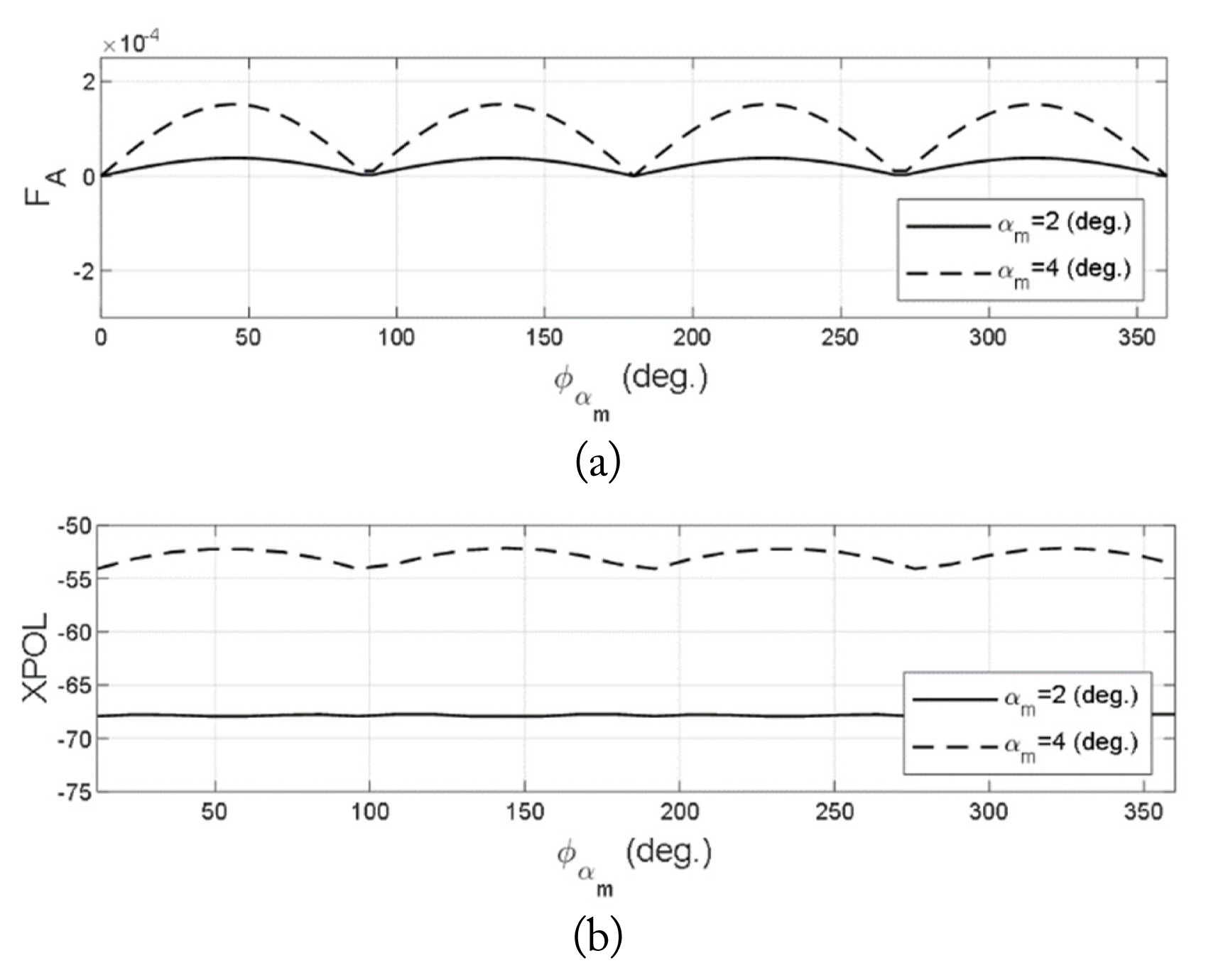
Here, F_A refers to the integration of the cross-pol component divided by an incident field from the feeder. From F_A, we can easily estimate the level of cross-pol radiation for various configurations of the misalignment error. Since F_A= 0 for the uniform misalignment error, the cross-pol level is very low. For a 1-cycle misalignment error with a cosine variation, F_A = 0 when φ_α_{_m}=0, although F_A≠ 0 and the cross-pol level increases when φ_α_{_m}≠0.

Moreover, for 1-cycle misalignments, a closed-form expression of F_A can be obtained from α in (8). A smooth change in the misalignment angle is assumed and φ_f is used instead of φ_k. By implementing Taylor’s series, P_t² is expanded into two terms, expressed as follows:

(10)

Pt2=sin2 α≅α2-α43.

Substituting (10) in (9), F_A for a 1-cycle misalignment error with a maximum misalignment angle of α_m at φ_α_{_m} is expressed as:

(11)

FA=12π|[(αm2)2π4-(αm2)2π48(27+cos 2 φαm)] sin 2 φαm|.

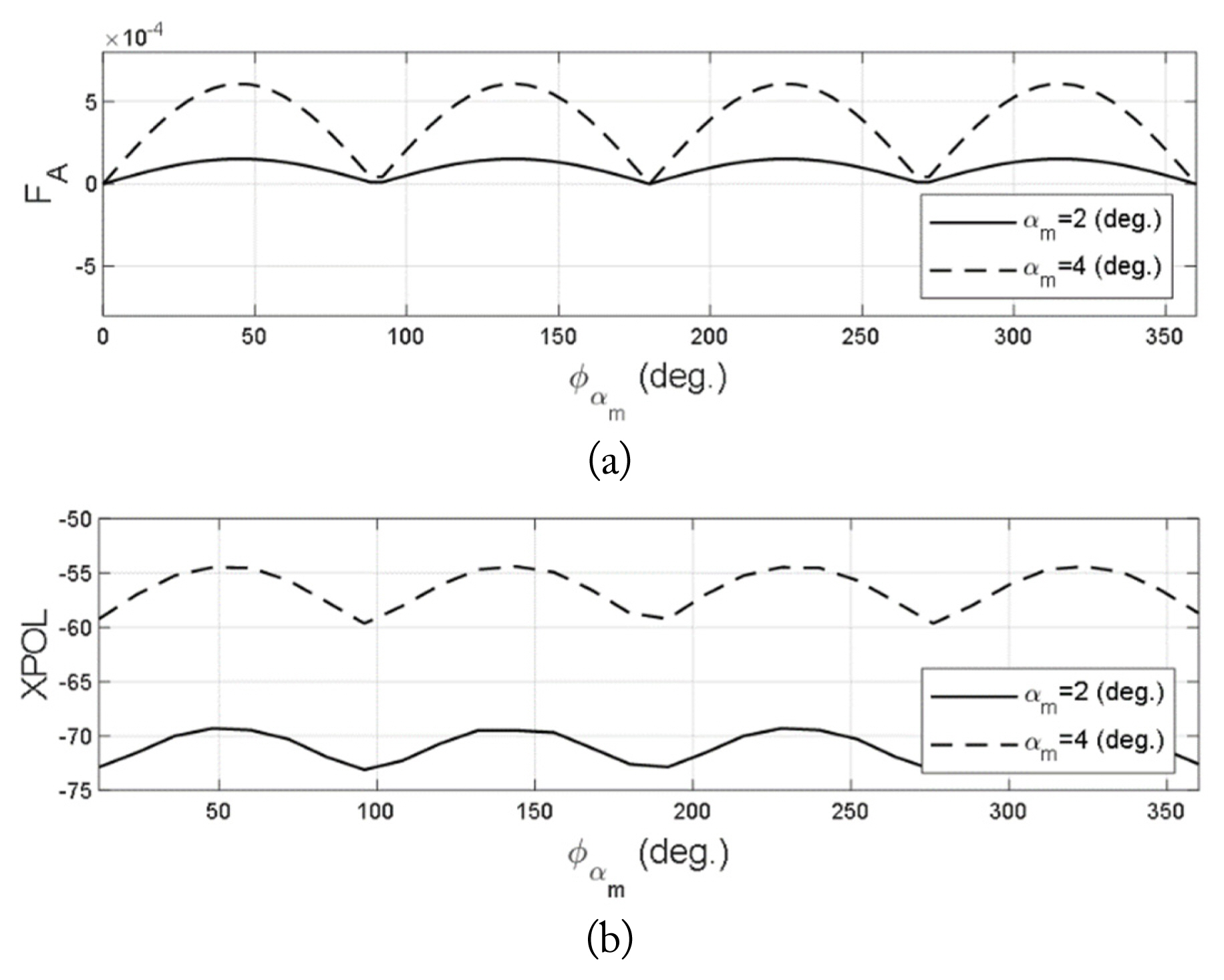
Fig. 8(a) shows the calculated F_A with respect to the change in φ_α_{_m} when α_m is 2° and 4°. It is observed that F_A changes along with φ_α_{_m}, reaching its maximum value when φαm=π4(2n-1), n=1, 2, 3, 4 and minimum when φαm=nπ4, n=1, 2, 3, 4. Fig. 8(b) shows the change in the XPOL of the far-field radiation. When α_m is 2°, the cross-pol level in the far-field radiation is low, while the change in φ_α_{_m} is small. However, when α_m is 4°, it is clearly observable that φ_α_{_m}'s for maximum and minimum of XPOL coincide with those of F_A. Effectively, the analysis of the cross-pol component in the aperture indicates that it is possible to minimize the level of cross-pol radiation by adjusting the angular position of maximum misalignment in a 1-cycle non-uniform error.

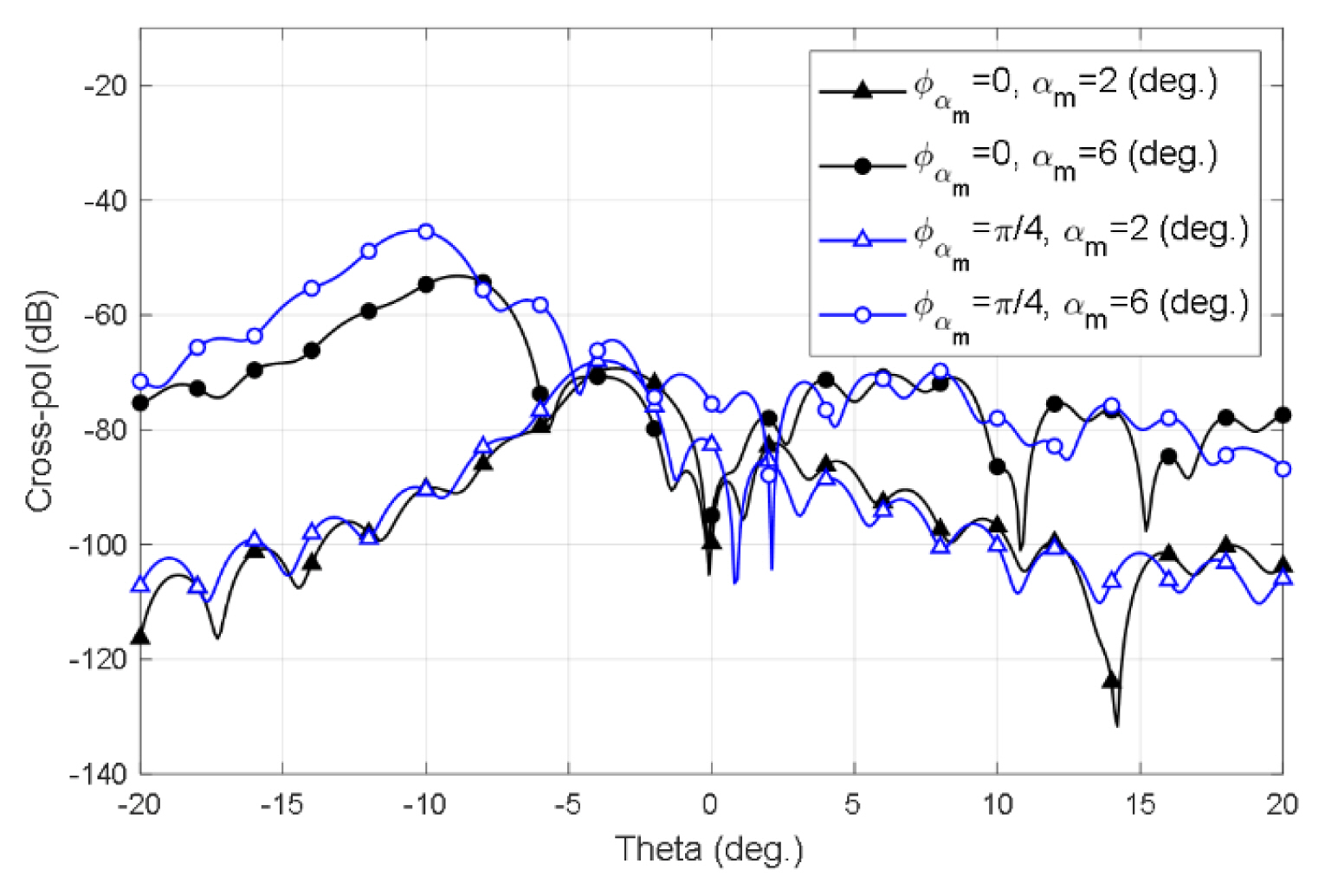
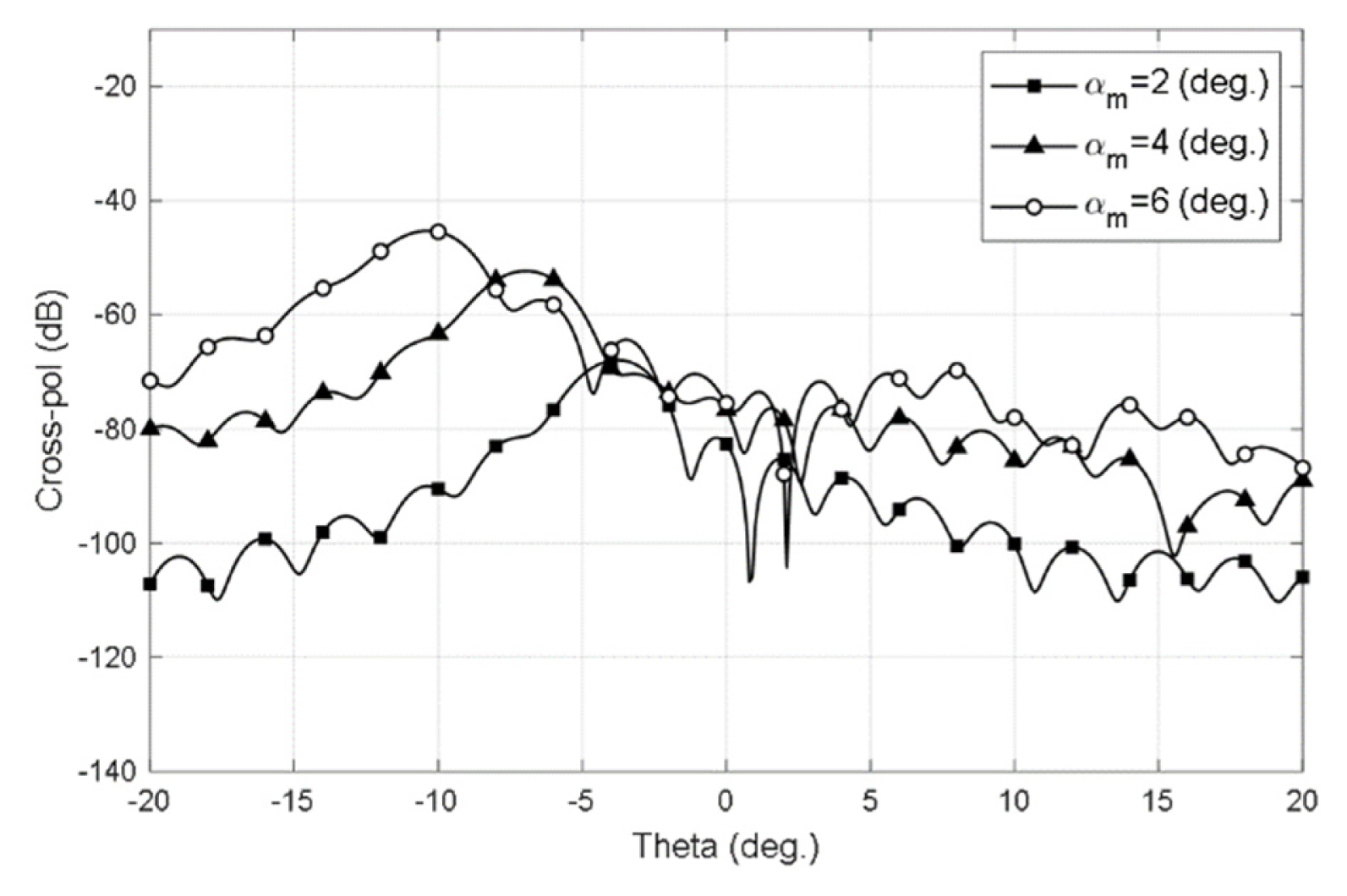
Fig. 9 depicts the cross-pol patterns in the φ=π4 plane for α_m = 2°, 4°, and 6°. The XPOL is −68 dB when α_m is 2°, while it increased to −45 dB when α_m is increased to 6°. Notably, the XPOL increased by more than about 7 dB compared to the uniform misalignment error. This indicates that the cross-pol radiation for the 1-cycle misalignment error is higher since the average of the cross-pol components in the aperture does not vanish.

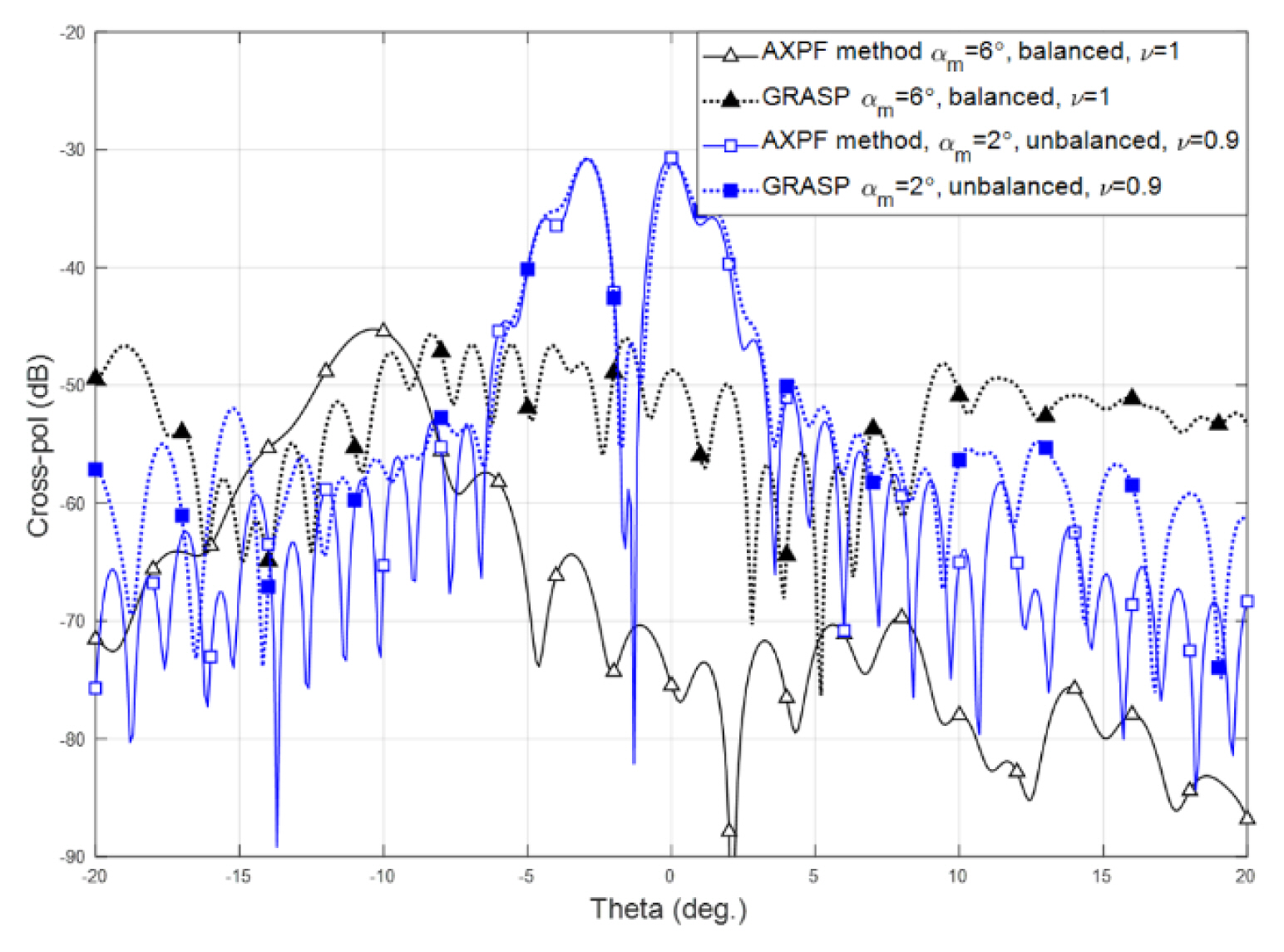
In Fig. 10, cross-pol patterns calculated by the AXPF method are compared with the results of physical optics approximation using the commercial GRASP program for one-cycle non-uniform errors. In the case of the unbalanced Gaussian feeder, in which the ratio of the standard deviations of C_H and C_E is v, the cross-pol patterns of the two methods show good agreement. The agreement between the results from the two methods in the unbalanced case implies that our analysis is valid for calculating cross-pol. In the balanced case, however, the level of cross-pol radiation is very low compared to that in the unbalanced case. Moreover, the patterns do not exhibit good agreement. The results of deploying the AXPF method clearly indicate tilting of the radiation field due to non-uniform panel misalignment. Apart from this, the AXPF analysis also provides adequate results with regard to the level of cross-pol radiation resulting from panel misalignments. Additionally, it demonstrates the physical implications for the generation of cross-pol components from panel misalignments.

2.2. 2-Cycle non-uniform misalignments

For N = 2, α_k varies across two cycles with regard to the change in φ_k from 0 to 2π, as shown in Fig. 11. When φ_α_{_m}= 0, the misalignment error reaches its maximum value at the 1st and 16th panels, and a minimum value at the 8th and 23rd panels. The configuration of the misalignment error is symmetric about the x- and y-axes. Meanwhile, the radiation patterns are symmetric, but vary in tandem with different angles of the observation planes. For φαm=π4, the error distribution is rotated, as shown in Fig. 11.

The distribution of A_CX in the aperture on the occurrence of a 2-cycle non-uniform misalignment is elaborated in Fig. 12(a) and 12(b), where α_m is 2°. These distributions are observed to be point symmetric about the center. For φ_α_{_m}=0, the net amount of A_CX is zero, while the cross-pol radiation is very small. However, for φαm=π4, the negative quantities in the 1st and 3rd quadrants prevail over the positive ones in the 2nd and 4th quadrants, as shown in Fig. 12(b). The noticeable net amount of cross-pol in the aperture is the cause of the high levels of cross-pol radiation for φαm=π4. Fig. 12(c) illustrates the change in A_CX in the φ_f-direction. It is clear that the average of A_CX is zero for φ_α_{_m}=0, but it does not completely vanish in the case of φαm=π4.

For the 2-cycle panel misalignment error (N = 2), we obtained the expression of the factor of the average cross-pol in the aperture F_A using (8) and (10).

(12)

FA=12π|[(αm2)2π-(αm2)476π] sin 2 φαm|.

Fig. 13(a) illustrates changes in F_A with φ_α_{_m} for N = 2, with F_A reaching its maximum value when φαm=π4(2n-1), n= 1, 2, 3, 4. The variation in F_A shows a similar feature as that in the case of N = 1, although the magnitude of F_A is larger for N = 2. The change in XPOL in the far field is shown in Fig. 13(b), which confirms that the φ_α_{_m} generating the maximum and minimum XPOLs coincides with the generation of the maximum and minimum F_A in the aperture.

Fig. 14 shows the cross-pol patterns in the φ=π4 plane for α_m = 2°, 4°, and 6°. When a 2-cycle misalignment error occurs, the cross-pol radiation pattern splits into two since these patterns are symmetric, and the peak value is lowered. Compared to the 1-cycle error, F_A for N = 2 is larger, but XPOL is lower by about 2 dB.

IV. Conclusion

This study first assumed the shape of the panel misalignment error that can occur in a deployable reflector antenna and then analyzed the generation mechanism of the cross-pol radiation caused by the panel misalignment error. The aperture field was calculated by considering the phase error of the signal and the rotation of the normal vector on the reflective surface resulting from the misalignment of the panel. The rotation of the normal vector caused by misalignment is an essential factor in the analysis of cross-pol performance. Moreover, the net amount of the cross-pol component in the aperture was found to be closely related to the level of cross-pol radiation. For non-uniform misalignment, the cross-pol radiation was higher, and the maximum cross-pol level was generated when φαm=π4(2n-1), n= 1, 2,3, …. It was also noted that the XPOL for the 2-cycle misalignment is higher by a maximum of 7 dB than that in the uniform misalignment, with α_m being 3°. Overall, the present method of analysis provides a design rule for deployable antennas, along with instructions for reducing the level of cross-pol radiation by adjusting the features of panel misalignment.

Acknowledgments

This work has been supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2020R1F1A107675512).

Fig. 1

(a) Rotation of the normal vector due to panel misalignment. (b) Normal vector on the r_f–θ_f plane.

Fig. 2

Generation of the components of t^due to panel misalignment.

Fig. 3

Distribution of A_CX in the aperture for the uniform misalignment error where α is 1°.

Fig. 4

Cross-pol radiation patterns for uniform misalignment errors of panels in the φ=π4 plane.

Fig. 5

α for 1-cycle misalignment errors.

Fig. 6

Distribution of A_CX in the aperture for 1-cycle misalignment errors when α_m is 2° for (a) φ_α_{_m} =0, (b) φαm=π4 , and (c) the magnitude changes with φ_f.

Fig. 7

Cross-pol radiation patterns for 1-cycle misalignment errors of panels in the φ=π4 plane for φ_α_{_m} =0 and π4

Fig. 8

Comparison with respect to φ_α_{_m} for 1-cycle misalignment errors of (a) F_A and (b) XPOL.

Fig. 9

Cross-pol radiation patterns for 1-cycle misalignment errors of panels in the φ=π4 plane.

Fig. 10

Comparisons of cross-pol patterns by GRASP using our method for analyzing the 1-cycle misalignment errors of panels in the φ=π4 plane for balanced and unbalanced feeders.

Fig. 11

α for 2-cycle misalignment errors.

Fig. 12

Distribution of A_CX in the aperture for 2-cycle misalignment errors when α_m is 2° for (a) φ_α_{_m} =0, (b) φαm=π4 , and (c) the magnitude changes with φ_f.

Fig. 13

Comparison with respect to φ_α_{_m} for 2-cycle misalignment errors of (a) F_A and (b) XPOL.

Fig. 14

Cross-pol radiation patterns for 2-cycle misalignment errors of panels in the φ=π4plane.

References

1. T. K. Lee, "Design of deployable lightweight antenna for satellite SAR," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 25, no. 11, pp. 1104–1112, 2014.

2. A. Miura and Y. Rahmat-Samii, "Analysis of mesh reflector antennas with complex mesh surfaces using physical optics combined with periodic method of moments," In: Proceedings of 2005 Asia-Pacific Microwave Conference; Suzhou, China. 2005.

3. C. Tienda, N. Bertl, M. Younis, and G. Krieger, "Characterization of the cross-talk SAR image produced by the cross-polarization in a single offset parabolic reflector," In: Proceedings of 2015 9th European Conference on Antennas and Propagation (EuCAP); Lisbon, Portugal. 2015, pp 1–4.

4. S. E. Park and S. G. Lee, "On the use of single-, dual-, and quad-polarimetric SAR observation for landslide detection," ISPRS International Journal of Geo-Information, vol. 8, no. 9, article no 384, 2019. https://doi.org/10.3390/ijgi8090384

5. W. L. Stutzman and G. A. Thiele, Antenna Theory and Design. 3rd ed. NJ: John Wiley & Sons, 2012.

6. S. S. Yoon, J. W. Lee, T. K. Lee, and J. H. Roh, "Insensitivity characteristics in the dual polarization of deployable CFRP reflector antennas for SAR," IEEE Transactions on Antennas and Propagation, vol. 66, no. 1, pp. 88–95, 2018.

7. J. Y. Lee, S. S. Yoon, S. H. Kim, T. K. Lee, J. W. Lee, J. H. Roh, and D. W. Yi, "Performance of solid surface deployable antenna for panel misalignment," In: Proceedings of 2016 URSI Asia-Pacific Radio Science Confer20ence (URSI APRASC); Seoul, South Korea. 2016, pp 877–879.

8. Y. Rahmat-Samii, "An efficient computational method for characterizing the effects of random surface errors on the average power pattern of reflectors," IEEE Transactions on Antennas and Propagation, vol. 31, no. 1, pp. 92–98, 1983.

9. S. J. Jo, J. Y. Lee, S. S. Yoon, T. K. Lee, and J. W. Lee, "Panel misalignment effects on the radiation pattern from a solid surface deployable antenna," Journal of Electromagnetic Engineering and Science, vol. 19, no. 4, pp. 253–258, 2019.

10. S. J. Jo Sia Lee, T. K. Lee, and J. W. Lee, "Effects of panel misalignment on polarization characteristics of deployable reflector antenna," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 19, no. 4, pp. 253–258, 2020.

11. A. Ludwig, "The definition of cross polarization," IEEE Transactions on Antennas and Propagation, vol. 21, no. 1, pp. 116–119, 1973.

Appendices

Appendix A.

Derivation of the formula for the electric field distribution at the aperture with panel misalignment

Eq. (3) in Section II indicates the electric field distribution at the aperture. By substituting (1) and (2) into E_r = 2(n^' · E_i)n^' – E_i, the reflected field in the aperture is given by:

(A.1)

Ea=V0e-jk2FrfC(θf)[-r^f cos φf sin(θf-2α)-θ^f cos φf cos(θf-2α)+φ^f sin φf].

The aperture field expressed in the spherical coordinates is transformed into one in the cartesian coordinates and expressed as follows:

(A.2)

Ea=V0e-jk2FrfC(θf)×[-cos φf sin(θf-2α)(x^f sin θf cos φf+y^f sin φf sin φf+z^f cos θf)-cos φf cos(θf-2α)(x^f cos θf cos φf+y^f cos φf sin φf-z^f sin θf)+sin φf (x^f sin φf+y^f cos φf)].

Finally, the formula for the electric field distribution in the aperture is derived by simplifying (A.2) in the (x,y,z) coordinates depicted in Fig. 1(a) as:

(A.3)

Ea(θf,φf)=V0e-jk2FrfC(θf)×[x^(2 sin2 α cos2 φf-1)-y^ sin2 α sin 2 φf-z^ cos φf sin 2 α].

Biography

Si-A Lee received her B.S. and M.S. degrees in electronics and information engineering from Korea Aerospace University, Goyang, Korea, in 2019 and 2021, respectively. She is currently a junior researcher at Satellite System Team 1 in Hanwha Systems. Her current research interests include satellite communication antennas and radar antenna design and analysis.

Biography

Seung-Joo Jo received her B.S. and M.S. degrees in electronics and information engineering from Korea Aerospace University, Goyang, Korea, in 2018 and 2020, respectively. She is currently a junior researcher at Satellite System Team 1 in Hanwha Systems. Her current research interests include satellite communication antennas and radar antenna design and analysis.

Biography

Suk-Jin Kim received his B.S. and M.S. degrees in electronics and information engineering from Korea Aerospace University, Goyang, Korea, in 2020 and 2022, respectively. His current research interests include satellite communications and radar antennas, spaceborne SAR systems, and antenna design and analysis.

Biography

Taek-Kyung Lee received his B.S. degree in electronic engineering from Korea University, Seoul, Korea, in 1983, and his M.S. and Ph.D. degrees in electrical engineering from the Korea Advanced Institute of Science and Technology (KAIST), Daejeon, Korea, in 1985 and 1990, respectively. From 1990 to 1991, he was a postdoctoral fellow at the University of Texas at Austin, TX, USA, under a grant from the Korea Science and Engineering Foundation. From 1991 to 1992, he was a research scientist at KAIST. In 1992, he joined the faculty of Korea Aerospace University (KAU), Goyang, Korea. He was an associate visiting research professor at the University of Illinois at Urbana–Champaign, IL, USA, from 2001 to 2002. From 2006 to 2007, he was the chairman of the School of Electronics, Information, and Computer Engineering at KAU, where he also held the position of director of the Aerospace and Aviation Electronics Research Center from 2011 to 2013. He was the chairman of the Radar Technical Group, Korean Institute of Electromagnetic Engineering and Science, Seoul, from 2012 to 2013, and served as the president of this institute in 2014. He is currently a professor at the School of Electronics and Information Engineering at KAU. His current research interests include computational electromagnetics, antennas, microwave passive circuits, satellite antennas, spaceborne SAR systems, and air surveillance systems.

Biography

Jae Wook Lee received his B.S. degree in electronic engineering from Hanyang University, Seoul, Korea, in 1992, and his M.S. and Ph.D. degrees in electrical engineering with a specialization in electromagnetics from the Korea Advanced Institute of Science and Technology, Daejeon, Korea, in 1994 and 1998, respectively. From 1998 to 2004, he was a senior member of the Advanced Radio Technology Department, Radio and Broadcasting Research Laboratory, Electronics and Telecommunications Research Institute, Daejeon. Additionally, he has been on the faculty of Korea Aerospace University (KAU), Goyang, Korea. He is currently a professor at the School of Electronics and Information Engineering at KAU. His current research interests include high power amplifier design, computational electromagnetics, electromagnetic interference and electromagnetic compatibility analysis on printed circuit boards, satellite antennas, and spaceborne SAR systems.