I. Introduction
Phase noise is the frequency-domain representation of a random fluctuation in the phase of a waveform. More precisely, it is defined according to the IEEE [1] as
where Ps, Pn, and fm represent the total signal power, the power density in one phase noise modulation sideband per Hz, and the offset frequency, respectively. When constructing a communication system, the phase noise performance of a source is generally an important specification that must be considered [2ŌĆō4]. However, accurate phase noise measurement remains an extremely challenging task.
Analog phase noise measurement methods can be classified into three: direct spectrum method, frequency discriminator method, and phase detector method [5, 6]. The direct spectrum method, the simplest method for measuring phase noise, uses a spectrum analyzer [5]. This method is unsuitable for measuring oscillators with ultra-low phase noise performance, as the noise floor of the instrument is comparatively high. In the frequency discriminator method, the frequency fluctuations of a signal are translated to low-frequency voltage fluctuations that can then be measured using a baseband analyzer. The phase noise is thus measured from the frequency fluctuations. This method is suitable for free running oscillators, such as LC oscillators or cavity oscillators [5].
In the phase detector method [5, 6], the most widespread method for measuring phase noise, a voltage-controlled oscillator with a low phase noise is necessary for the reference source, which is phase locked to an SUT (source under test) using a narrowband feedback loop. In the locked state, the reference source has the same frequency as the SUT and maintains a phase quadrature. The phase detector detects the phase difference of the SUT from the reference source, which corresponds to the phase noise. The phase detector method can measure extremely low phase noise with a good reference source. Using two-channel correlation, the phase noise floor of the phase detector method can be further improved: it can be further lowered by about 20 dB [5]. Today, combining the previous methods, state-of-the-art phase noise measurement equipmentŌĆöthat shows a phase noise floor close to ŌłÆ180 dBc/Hz at a far-out offset frequency of >1 MHz [7, 8]ŌĆöis available on the market.
Digital phase noise measurement systems began gaining interest for their suitability as a cheap automatic test equipment in mass-production tests [9]. In a digital phase noise measurement system, the SUT signal is digitally sampled, and its phase is detected using a digital quadrature demodulator. A simple fast Fourier transform (FFT) operation on the SUTŌĆÖs detected phase results in the phase noise. However, the phase noise floor of digital phase noise measurement systems is generally quite higher than that of the best analog phase noise measurement system. Furthermore, the frequency range of the digital phase noise measurement system is basically limited to low frequencies of about tens of MHz range.
Significant improvement in the phase noise floor of the digital phase noise measurement systems can be achieved by removing the ADC clock jitter noise [10]. The work in [10] used four identical ADCs characterized by 14 bits or more, and the two-channel cross correlation technique was applied to suppress the ADC noise after the ADC clock jitter removal. The work, implemented using FPGAs and DSPs, achieved a phase noise floor of about ŌłÆ170 dBc/Hz. However, the SUT frequency range of the work is still limited to the frequency range of 1ŌĆō30 MHz. Due to the low-frequency range, it must be used in conjunction with a down converter to measure the phase noise of SUTs at higher frequencies. Several studies have been conducted to extend digital phase noise measurement systems to higher frequencies using subsampling or downconverters [11ŌĆō13].
In this study, we aimed to measure phase noise using a digital oscilloscope. It offers easier hardware implementation than FPGA and DSP implementation for a digital phase noise measurement system. Moreover, it may allow the realization of cheap automatic solutions that can be released as a software option. Furthermore, the ADCs in the digital oscilloscope usually have a wide bandwidth up to several gigahertz, and the phase noise of a high frequency SUT for communication systems can be measured without external downconverters. However, a digital oscilloscope has nominally a 10-bit resolution, which inevitably results in poor phase noise floor. The phase noise sensitivity using the digital oscilloscope is usually poor and is above ŌłÆ110 dBc/Hz [14]. In this paper, we provide a digital noise measurement system using a 10-bit digital oscilloscope with a phase noise sensitivity of about ŌłÆ160 dBc/Hz.
Second, we present a novel analysis of the measured phase noise. As a result, the ADC clock jitter noise and the thermal phase noise floorŌĆöthe phase noises added by an ADCŌĆöcan be identified. The analysis leads to the novel cross correlation method capable of extracting the true SUT phase noise alone. Consequently, the true SUT phase noise can be obtained by removing the phase noises added by the ADC. In addition, the proposed method, unlike the previous works, does not need a reference signal whose phase noise is low enough compared to the SUT phase noise. The proposed method alleviates the choice of the reference source, and the optimal reference source frequency can be freely selected. In this paper, under the previously explained motivation, we present a novel phase noise measurement method using the digital oscilloscope MXR608A [15] from Keysight Technologies.
II. Phase Noise Measurement System
1. Configuration
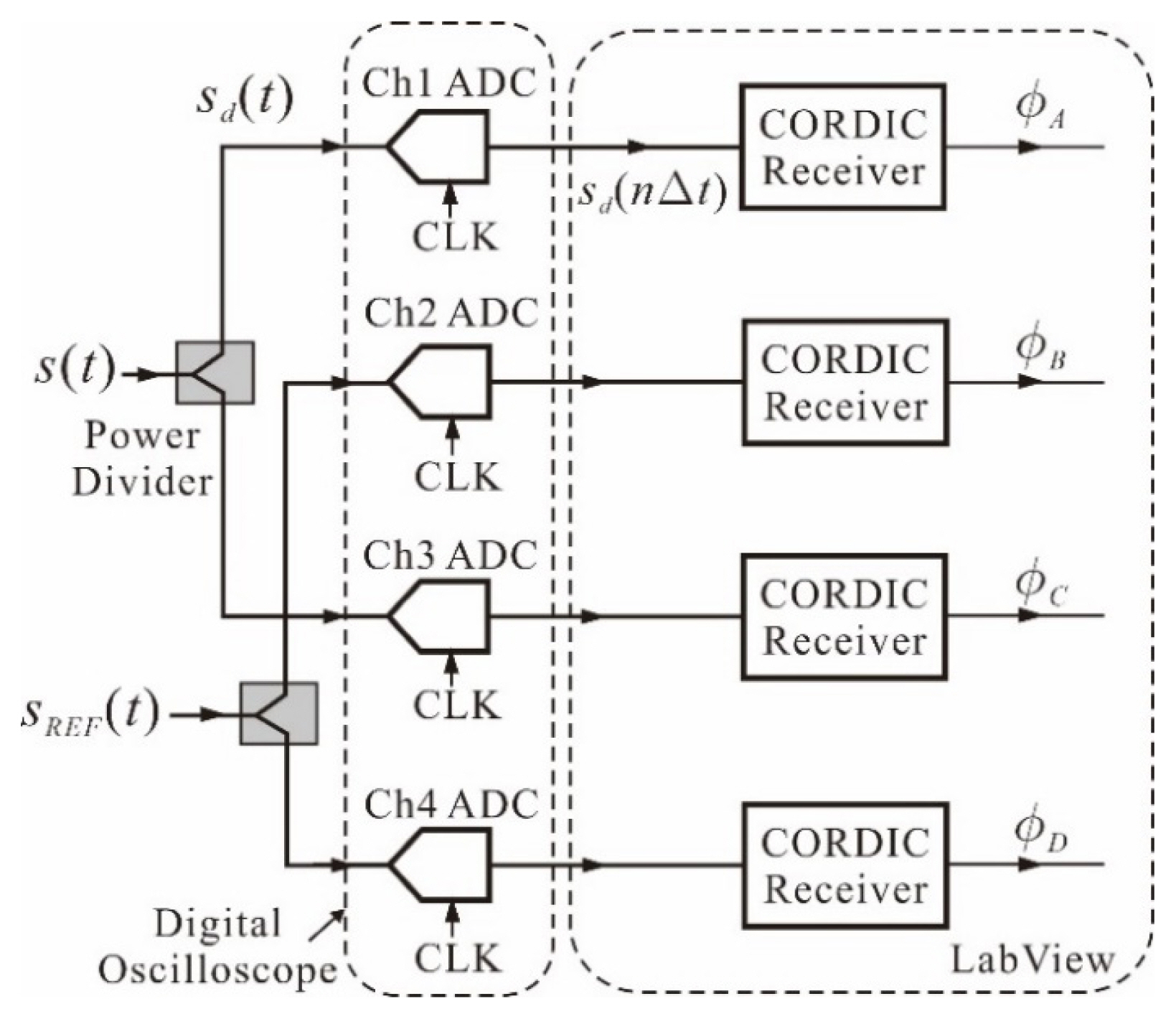
Fig. 1 shows our phase noise measurement system configuration. The analog time domain signals s(t) and sREF(t) in Fig. 1 represent the SUT and reference signals. The four ADCs represent the four channels of the digital oscilloscope MXR608A from Keysight Technologies. The two power dividers, ZFRSC-183ŌĆōS+ from Mini Circuits, divide s(t) and sREF(t). The divided s(t) and sREF(t) are applied to channels 1, 3 and 2, and 4 of the digital oscilloscope, respectively, and they are sampled at every ╬öt. The sampling frequency fs is thus (╬öt)ŌłÆ1.
The USB device port of MXR608A is connected to the host PC. The sampled channel data is first stored in the memory of MXR608A, and the stored data is read into the PC using the LabView of National Instruments. The length NL of the sampled channel data that can be read into a PC is limited by both the memory size and the Labview data processing capacity. In our setup, NL is limited by the LabView data processing capacity, and the maximum NL is about 4M samples. Both NL and fs determines the frequency range and resolution of the Fourier transform of the data read into PC. The frequency range is given by
1 2 f s
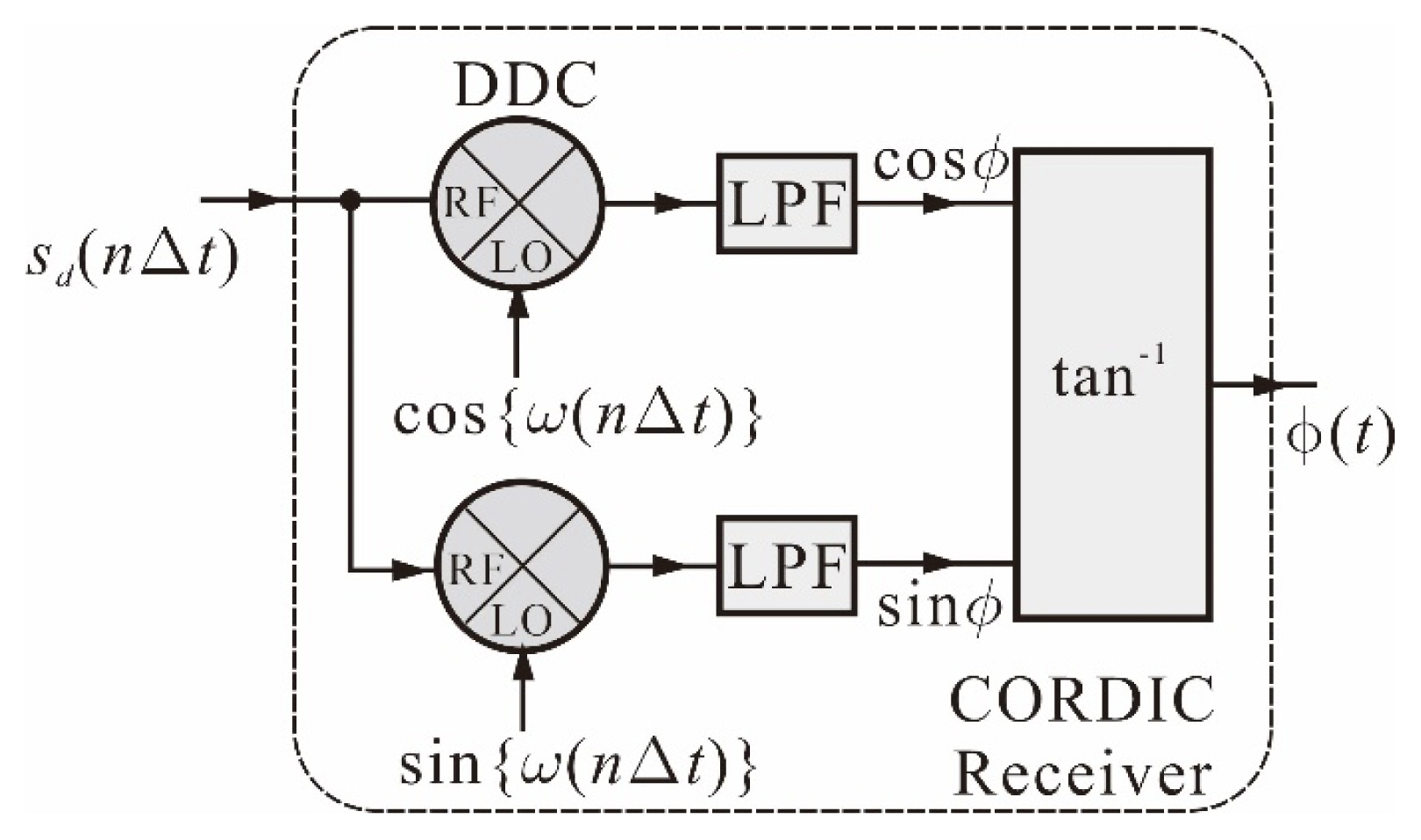
Fig. 2 shows the detailed CORDIC (coordinate rotation digital computer) [16, 17] receiver in Fig. 1. The CORDIC receiver is implemented using LabView and it detects the phase of the data read into the PC. The digital-down converters (DDC) is a multiplier that takes the product of two waveforms. The Žē of sd(n╬öt) was detected using Extract Single Tone Information.vi (virtual instrument) of LabView. The orthogonal LO signals cos{Žē(n╬öt)} and sin{Žē(n╬öt)}, where Žē is equal to that of sd(n╬öt) were generated using Sine Waveform.vi of LabView. The two DDCs produce cosŽå and sinŽå. The phase Žå is obtained by taking the tanŌłÆ1 operation. In FPGA programming, Žå is obtained from cosŽå and sinŽå by iterative calculation using the CORDIC algorithm. However, in LabView implementation, Žå is simply obtained using a tanŌłÆ1 operation, and implementing the CORDIC algorithm is unnecessary.
At the DDC output, the second harmonic appears. In addition, since cosŽå and sinŽå change slowly, the decimation of the higher input sample rate is necessary. The lowpass filter (LPF) in Fig. 2 both removes the second harmonic and decimates the input sample rate. The digital infinite impulse response (IIR) elliptic LPF is then added for the second harmonic rejection. After the digital IIR elliptic LPF, decimation is achieved using Waveform Resample.vi of LabView. Fig. 3 demonstrates the phase noise measurement system.
2. Phase Spectrum
In Fig. 2, Žå is a time domain signal, and the phase spectrum SŽå(fm) [1] can be obtained from the power spectral density (PSD) of Žå. Finally, the phase noise L(fm) in (1) can be obtained from SŽå(fm) as
The cross-power spectrum for the two selected phase fluctuations from ŽåA, ŽåB, ŽåC, and ŽåD in Fig. 1 is frequently necessary to obtain the phase noise. The cross-power spectrum is obtained using the Cross Spectrum (Real-Im).vi in LabView. The cross-power spectrum of two random signals results in a complex number in the frequency domain, one having real and imaginary parts. Moreover, in this paper, the cross-power spectral density of ŽåA and ŽåB and its real and imaginary parts are denoted as X(ŽåB, ŽåB; fm) = RAB + jIAB. Thus, X(ŽåB, ŽåB; fm) is
In Eq. (3)F(┬Ę) represents the Fourier transform, and the top bar of F(┬Ę) the complex conjugate of the Fourier transform. ╬öf represents bandwidth, and w the equivalent noise bandwidth (ENBW) of window function. The real part RAB corresponds to the power spectrum due to the correlated parts of two random signals, while the imaginary part IAB represents the power spectrum due to the uncorrelated parts. RAB converges to a finite value, while IAB converges to zero as the average number of the cross-power spectrum increases.
The selected window in Eq. (3) is a seven-term Blackman Harris window and w = 2.63191. The spectral leakage of the four-term Blackman Harris window is known to be below about ŌłÆ90 dB. Taking the dynamic range of phase noise measurement into consideration, ŌłÆ90 dB may not be enough, and the seven-term Blackman Harris window, which yields a spectral leakage of about ŌłÆ150 dB, is selected [18].
Phase noise L(fm) is usually plotted on a log scale fm. However, SŽå(fm) is usually computed from equidistant time domain samples. As a result, SŽå(fm) is uniformly spaced on fm defined over [fstart, fstop]. When SŽå(fm) is plotted on a log scale fm, it is densely spaced at a higher fm, which results in higher fluctuation. The way to reduce the fluctuation of SŽå(fm) at higher fm is to increase its average number, particularly at a higher fm. Since the average number of SŽå(fm) increases as fm increases, the successively decimating FFT structure [19] is efficient for reducing the fluctuation of SŽå(fm) at higher fm. This structure is appropriate for FPGA implementation.
However, instead of using the successively decimating FFT structure, the fluctuation at higher fm can be efficiently reduced by increasing the averaging bandwidth as fm increases. Instead of linearly spaced fm defined over [fstart, fstop], a new set of log-spaced offset frequency, fm,log(n) can be defined on [fstart, fstop]. The n-th element of log-spaced offset frequency fm,log(n)=fstart10kn for a constant k and n = 0, ŌĆ”, N, where N is the number of log-spaced offset frequencies. For a newly defined log-spaced fm,log, the bandwidth BW can be defined to increase with fm,log as
where Q is constant, specifying the number of uniformly spaced spectrums to be included for averaging at fm,log(n). Now, the value of SŽå(fm,log) can be computed as the average of the spectrums SŽå(fm) within BW. Consequently, SŽå(fm,log) will show the reduced fluctuation at higher fm,log. Similar spectral estimation methods can be found in [20] and [21]. We named this the logarithmic bandwidth averaging (LBA), which is more efficient in LabView programming than the successively decimating FFT structure. The LBA is programmed using MATLAB and implemented using the MATLAB Script Node.vi in Lab-View.
III. ADC Phase Noises
The time domain phase fluctuations ŽåA, ŽåB, ŽåC, and ŽåD in Fig. 1 can be modeled simply by the sum of the phase fluctuations as follows:
In Eq. (5), Žåd and Žåref represent the SUT and reference signal phase fluctuations, while Žåc represents the phase fluctuation due to the ADC clock jitter. The constants a and b represent the scaling constants of the phase fluctuation due to the ADC clock jitter. Since the frequencies of the SUT and reference signal are generally different, the phase fluctuation due to the ADC clock jitter differs, as in Eqs. (5a) and (5b). The Žå1, Žå2, Žå3, and Žå4 represent the phase fluctuations originating from the quantization and thermal noises of the ADCs, which are almost white in the frequency domain. In addition, Žå1, Žå2, Žå3, and Žå4 are uncorrelated.
1. ADC Phase Noise Floor
The phase fluctuations Žå1, Žå2, Žå3, and Žå4 in Eq. (5) due to the ADC noises correspond to the phase noise floor for the digital phase noise measurement. Usually, instead of ADC phase fluctuations like Žåj (j = 1, 2, 3, or 4), ADC performance is characterized by signal-to-noise ratio (SNR). The ADC SNR is given by [22] as follows:
where B is the number of bits of the ADC, and fs is the sampling frequency (or sampling rate). The SNR in Eq. (6) can be used to estimate the measurable phase noise range at a higher fm because L(fm) in Eq. (1) can be interpreted as SNR. Thus, the SNR in Eq. (6) corresponds to the phase noise floor. In the case of the 10-bit digital oscilloscope, the value of the SNR is computed to be about ŌłÆ140 dBc/Hz for a sampling frequency of fs = 100 MHz. However, the real ADCs are imperfect and introduce additional noise and distortion. The SNR estimation by Eq. (6) shows a significant gap from the real SNR. The concept of the effective number of bits (ENOB) was introduced based on the measured SNR or SINAD. However, even the ENOB is not a true phase noise floor. In this paper, we propose the measurement method of the true phase noise floor PŽåj(fs) due to Žåj (j = 1, 2, 3, and 4) in Eq. (5) using the cross-correlation. The true phase noise floor PŽåj(fs) can be computed from the phase spectrum of SŽåj(fm) as
P Žå j ( f s ) = 1 2 S Žå j ( f m )
In Eq. (5), the correlated part between (ŽåA ŌĆō ŽåC) and ŽåA is only Žå1. Similarly, the correlated part between (ŽåA ŌĆō ŽåC) and ŽåC is only Žå3. Therefore, SŽå1(fm) and SŽå3(fm) are given by
Here, <┬Ę> represents the average operation and M is the average number. Now, the phase noise floors due to Žå1 and Žå3 are determined as
P Žå 1 ( f s ) = 1 2 S Žå 1 ( f m ) P Žå 3 ( f s ) = 1 2 S Žå 3 ( f m )
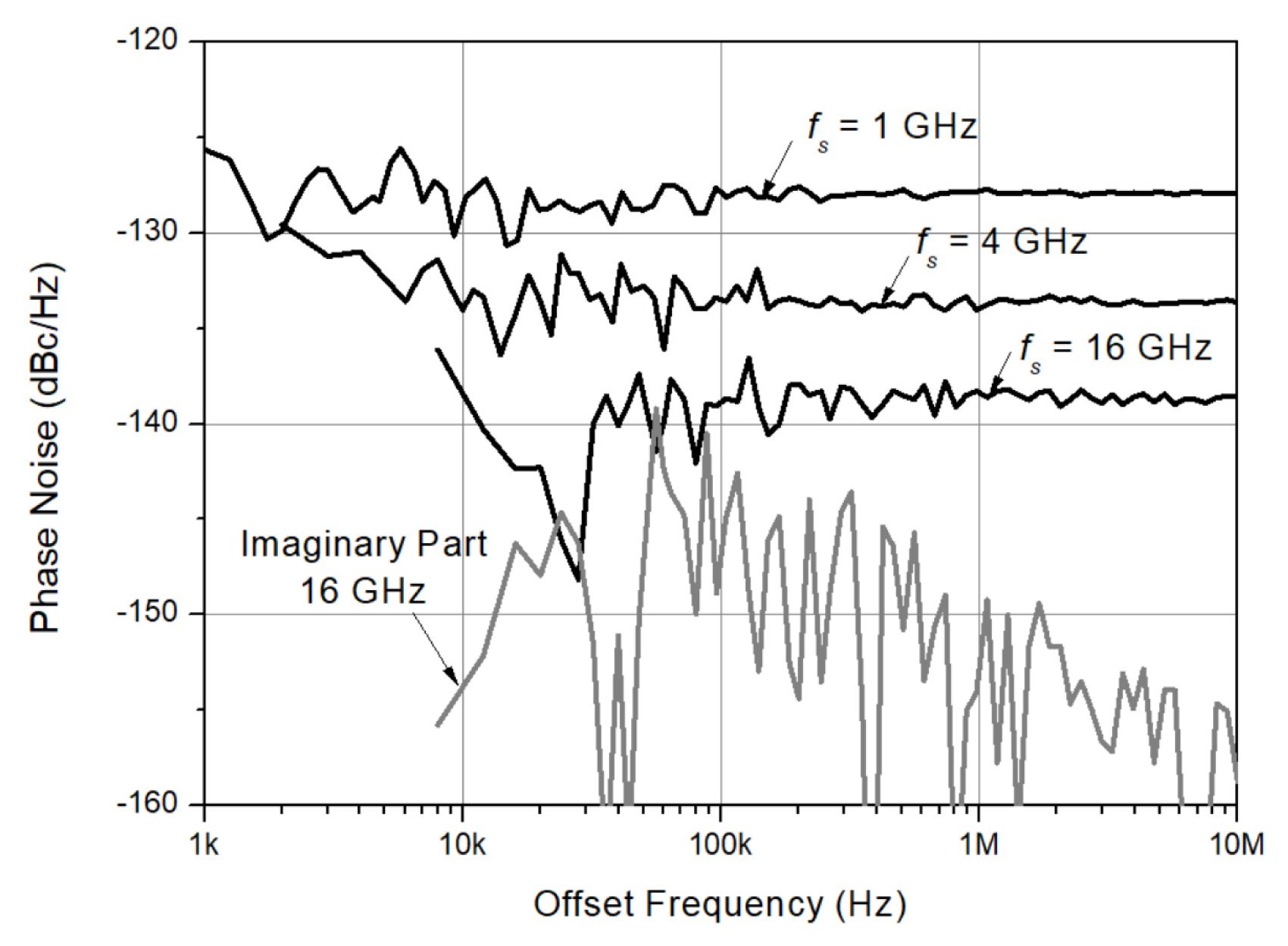
The measured phase noise floor values in Fig. 4 for fs = 1, 4, 16 GHz are about ŌłÆ128 dBc/Hz, ŌłÆ134 dBc/Hz, and ŌłÆ139 dBc/Hz (about ŌłÆ150 dBc/Hz, ŌłÆ156 dBc/Hz, and ŌłÆ162 dBc/Hz by Eq. (6)), respectively. As expected, the phase noise floor value predicted by Eq. (6) shows a significant gap. Since the digital oscilloscope has a 10-bit resolution, the phase noise floor is poor, as shown in Fig. 4, even though fs is set to several gigahertz. As fs increases, the phase noise floor is lowered and is about 6 dB down per one octave increase in fs. The measured PŽåj(fs) (j = 1, 2, 3, and 4) are almost equal. Thus, the phase noise floors at fs are denoted by PŽå1(fs) = PŽå2(fs) = PŽå3(fs) = PŽå4(fs) = PŽå(fs).
The phase noise floor limits the practically measurable phase noise range of an SUT. To simplify the explanation, we assume that the phase fluctuation due to ADC clock jitter is 0. In this case, Žåc = 0 for ŽåA and ŽåC in Eqs. (5a) and (5c). Under the assumption, the SUT phase noise SŽåd(fm) can be obtained from Ōī®X(ŽåA, ŽåC; fm)Ōī¬MŌåÆŌł×. Note that the X(ŽåA, ŽåC; fm) includes the cross-power spectrums of the uncorrelated terms as well as SŽåd(fm). As MŌåÆŌł×, the cross-power spectrums of the uncorrelated terms converge to 0, and SŽåd(fm) can be obtained. Therefore, the cross-power spectrums of the uncorrelated terms in X(ŽåA, ŽåC; fm) become the phase noise floor. It is known that the cross-power spectrum of two uncorrelated signals decreases by about 5 dB per a decade increase of M [23]. However, it is impossible to increase the average number MŌåÆŌł×. The time necessary for the cross-power spectrum average number M = 10,000 is about a day for a PC with a 3.6 GHz Intel i3 CPU and a RAM of 64 GB. We take the time necessary for the average number M = 10,000 as the practical time limit for the phase noise measurement. Therefore, the phase noise floor improvement using the cross-correlation technique is practically limited by 20 dB.
Under the assumption Žåc = 0, the phase noise floor for the cross-power spectrum X(ŽåA, ŽåC; fm) is determined by X(Žå1, Žå3; fm), which decreases with M as follows:
Since PŽå(fs) in Fig. 4 is about ŌłÆ128 dBc/Hz at a sampling frequency of fs = 1 GHz, Ōī®X(Žå1, Žå3; fm)Ōī¬M = 10,000 will be about ŌłÆ148 dBc/Hz. To decrease the phase noise floor further by 10 dB more requires a time of about 100 days, which is intolerable and impossible. Therefore, the phase noise of about ŌłÆ148 dBc/Hz for fs = 1 GHz is the limit value that can be measured using this setup. The SUT with the phase noise above ŌłÆ148 dBc/Hz at far-out offset frequencies can be measured, but the phase noise below ŌłÆ148 dBc/Hz cannot be measured. From Fig. 4, the measurable phase noise range for fs = 16 GHz is estimated to be about ŌłÆ160 dBc/Hz.
Lower phase noise can be measured by increasing the sampling frequency fs. However, to measure the phase noise at a lower offset frequency fm, the length of the sampled data NL should be increased in proportion to the increase in fs. The minimum offset frequency fm,min for a given sample data length NL is determined by
As explained in Section II-1, the sample data length NL cannot be increased without limit due to the LabView data processing capacity. As a result, a phase noise lower than the minimum offset frequency given by Eq. (9) cannot be measured.
2. Phase Noise due to ADC Clock Jitter
The ADC clock jitter also affects the phase noise of the sampled signal. To find this, the total phase ŽåT(t) of sd(t) in Fig. 1 is represented by
In Eq. (10), Žēd and Žåd are the frequency and phase of the SUT respectively. Note that Žåd randomly fluctuates. For an ADC sampling frequency Žēs = 2ŽĆfs, the time ts that sampling occurs is
In Eq. (11), ╬öt = 1/fs, and Žåc is the phase fluctuation caused by the phase noise of the ADC clock signal. Eq. (11) means that the sampling time ts jitters due to the phase fluctuation Žåc. Thus, ŽåA in Eq. (5a) without Žå1 due to the ADC clock jitter is
The last two terms Žåd and
Žē d Žå c Žē s
In this paper, we propose a method to verify the relation given by Eq. (13) using the cross correlation. The phase noise due to the ADC clock jitter can be obtained by averaging the cross-power spectrum of ŽåA and ŽåB as follows:
Similarly, averaging the cross-power spectrum of ŽåA and ŽåC
In Eq. (15)SŽåd(fm) is the SUT phase spectrum. When the SUT with a low phase noise is selected, Ōī®X(ŽåA, ŽåC; fm)Ōī¬MŌåÆŌł× can be approximated by a2SŽåc(fm) as in Eq. (15).
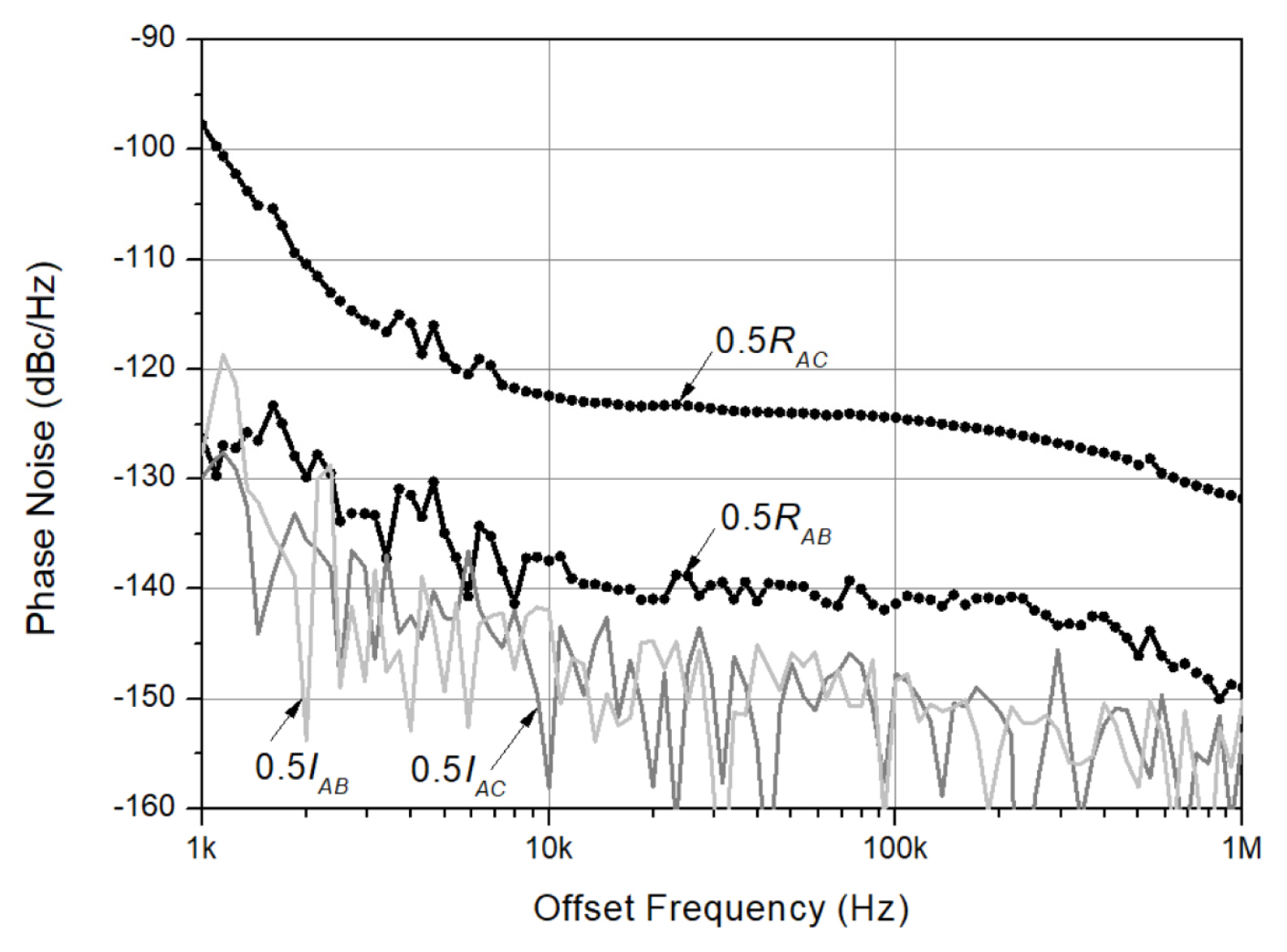
Fig. 5 shows RAB and RAC in Eqs. (14) and (15). The SUT and reference signal frequencies are 1.4151 GHz and 50 MHz, respectively. The synthesized signal generator E8257D [24] is used as the SUT signal, and 50 MHz OCXO from Wenzel Associates [25] is used as the reference signal. The sampling frequency is set to fs = 200 MHz, and the average number is set to M = 10,000. In Fig. 5, it can be found that the approximation holds because RAC = a2SŽåc(fm) is sufficiently larger than SŽåc(fm), the phase noise of 1.4151 GHz signal given in the datasheet.
From RAB and RAC in Eqs. (14) and (15), they have the same frequency dependence. Note that the frequency dependence of RAC and RAB on fm in Fig. 5 are found to be almost equal. Their ratio should be b/a = (50 MHz/1.4151 GHz)ŌłÆ1 = (28.3)ŌłÆ1 = ŌłÆ14.5 dB. To confirm b/a, the phase noise values are read from Fig. 5 at fm = 10 kHz. The phase noise values are ŌłÆ122.3 dBc/Hz and ŌłÆ137.4 dBc/Hz, respectively, and the difference is about ŌłÆ15.1 dB, which is close to the predicted value of b/a = ŌłÆ14.5 dB.
In the case of RAB, M should be sufficiently increased to attenuate the uncorrelated components in ŽåA and ŽåB. For fs = 200 MHz, the phase noise floor due to the ADC phase fluctuation is about ŌłÆ124.5 dBc/Hz, as explained in Section III-1. The proper average number M is estimated to be more than 105 to measure the phase noise of about ŌłÆ150 dBc/Hz. Consequently, the imaginary part of the cross-power spectrum is not sufficiently suppressed as shown in Fig. 5, and RAB shows a significant fluctuation.
IV. SUT Phase Noise Extraction
As explained in Section III, the SUT phase noise can be determined by removing the added ADC phase noises in Eq. (5). However, the removal is not simple, and the removal method was first proposed in [10]. Fig. 6 shows the block diagram of the method presented in [10]. As a result, they achieved the digital phase noise measurement system with a phase noise floor about ŌłÆ170 dBc/Hz for the frequency range of 1ŌĆō30 MHz. Based on the technique in [10], a digital phase/amplitude modulation (PM/AM) noise measurement system [11] and a full digital phase noise measurement system [12] have been developed. To explain the pros and cons of our method, comparing it with the method in [10], which we refer to as the traditional method, is necessary.
There may be several methods other than those shown in Fig. 6 to extract the SUT phase noise. When comparing the various methods, the question is about the properties of the cross-correlated output like SA(fm) in Fig. 6 and about the phase noise floor levels of Žå╬▒ and Žå╬▓ that are used to obtain the cross-correlated output. Note that the phase noise floor levels of Žå╬▒ and Žå╬▓ are different from those of ŽåA, ŽåB, ŽåC, and ŽåD as a result of the operation. Whether or not SA(fm) contains phase noises other than the SUT phase noise should be investigated because the phase noise contributions of the other phase noises should be subtracted to obtain the true SUT phase noise from SA(fm). In addition, as explained in Section III-1, the phase noise floor levels of Žå╬▒ and Žå╬▓ determine the measurable phase noise range. In this paper, the theoretical investigation on cross-correlated outputs and phase noise floor levels is presented. Based on the investigation, we propose a novel cross-correlation method for extracting the SUT phase noise.
1. Traditional Method
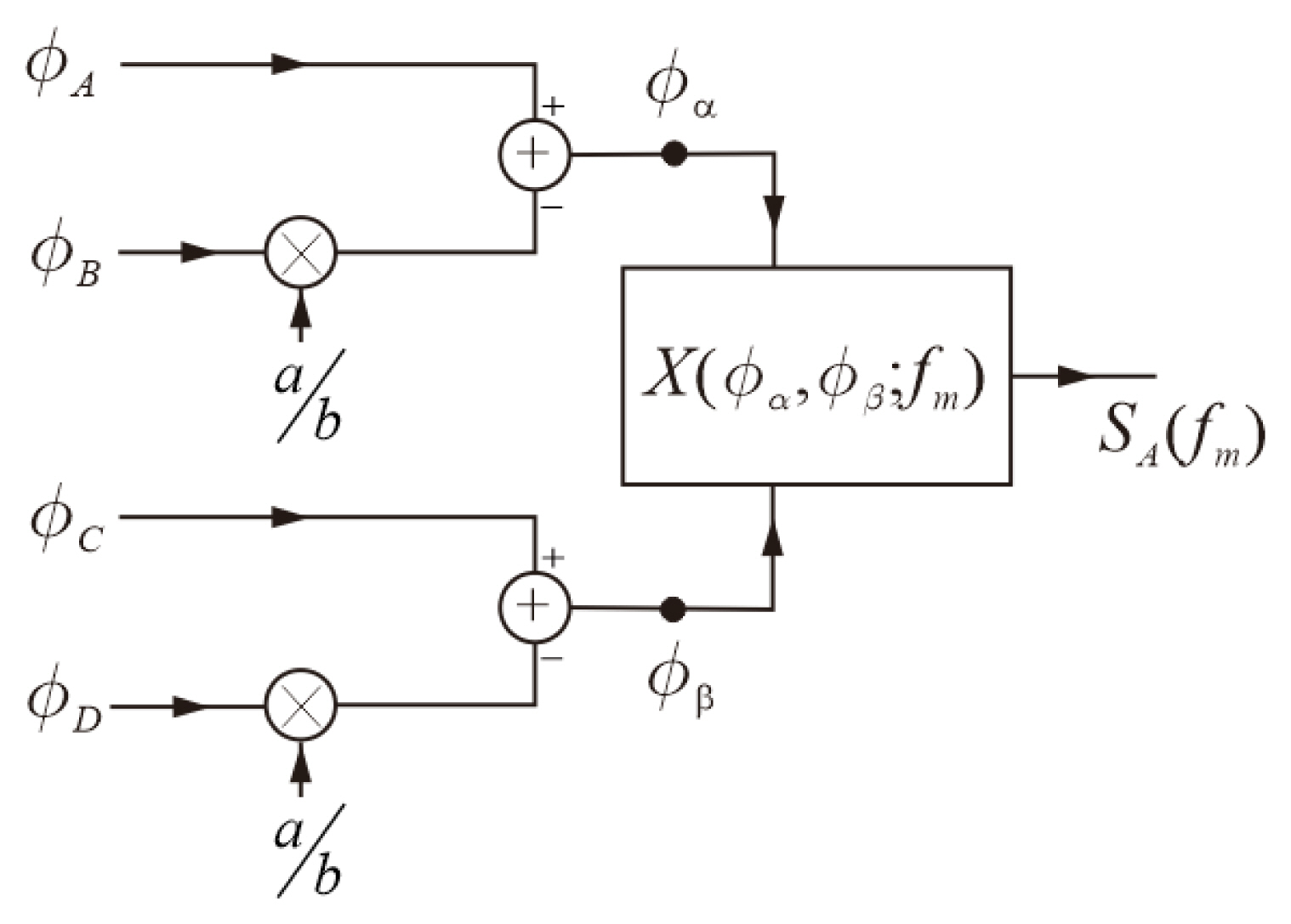
From Fig. 6, Žå╬▒ and Žå╬▓ are given by
As shown in Eq. (16), the correlated term is Žåd ŌĆō (aŽåref)/b, while UA and VA are uncorrelated. Therefore, the phase spectrum SA(fm) in Fig. 6 obtained from Ōī®X(Žå╬▒, Žå╬▓; fm)Ōī¬MŌåÆŌł× is
Notably, SA(fm) in Eq. (17) includes the reference signal phase noise scaled by
a 2 b 2
In addition, the phase noise floor for SA(fm) is determined by the cross correlation of UA and VA. From UA and VA in Eq. (16), the thermal phase noise floors are Žå1 ŌĆō (aŽå2)/b and Žå3 ŌĆō (aŽå4)/b. Thus, the cross correlation of UA and VA for the average number of M is
where PŽå(fs) is the phase noise floor value of Žåj (j = 1, 2, 3, and 4) explained in Section III-1. It should be noted that the phase noise floor rises from PŽå(fs) by the factor
1 + ( a b ) 2 1 + ( a b ) 2
In case that the SUTŌĆÖs frequency is lower than the reference signalŌĆÖs frequency, the factor (a/b) is small and the rising factor
1 + ( a b ) 2
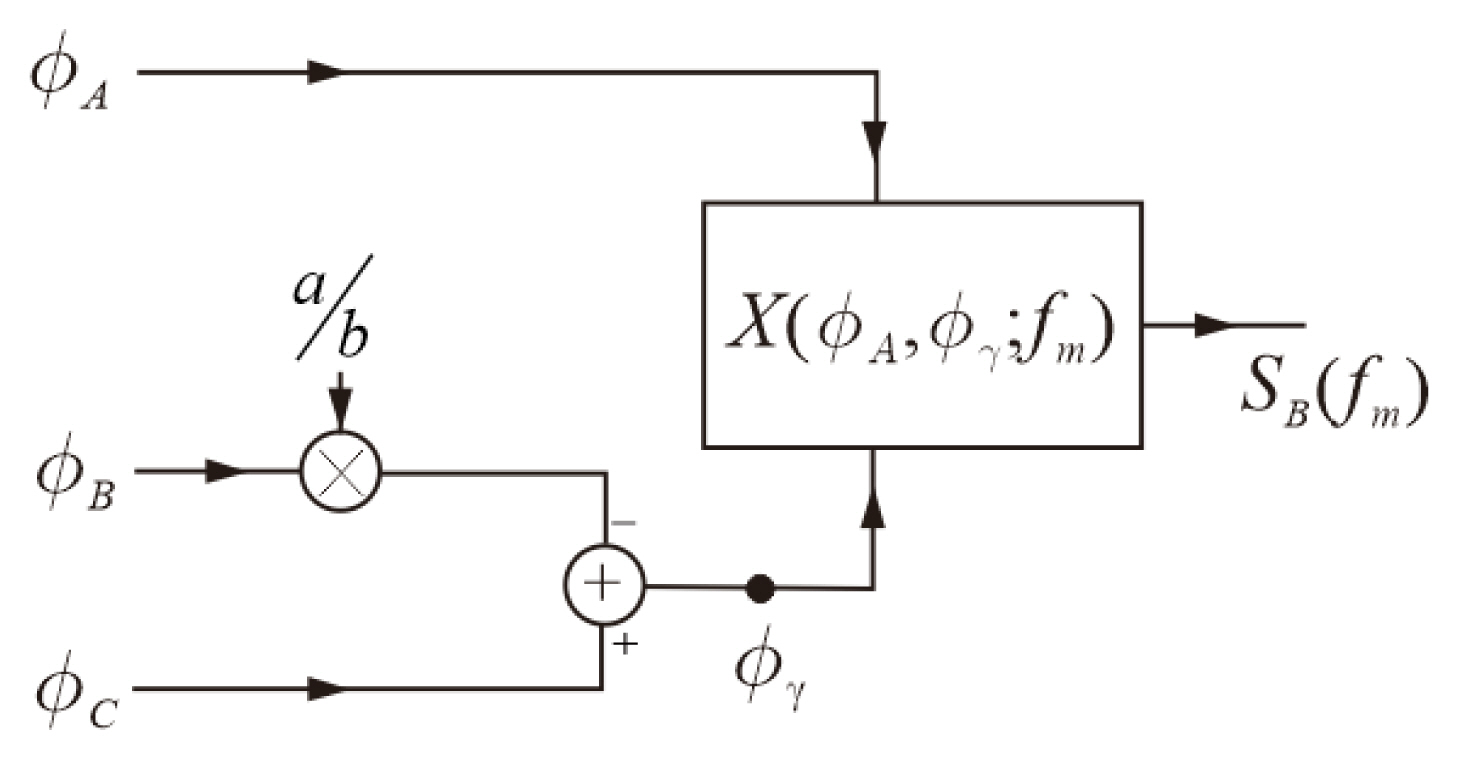
2. Proposed Cross-Correlation Method
From (19a) and (19b), the only correlated term is Žåd. Note that UB and VB are uncorrelated. Therefore, SB(fm) = Ōī®X(ŽåA, Žå╬│; fm)Ōī¬MŌåÆŌł× is given by
In contrast to SA(fm) in Eq. (17)SB(fm) does not contain the reference signal phase noise. Similarly, the phase noise floor for SB(fm) is determined by the cross correlation of UB and VB. Note that UB at higher fm is determined by Žå1 because aŽåc rapidly decreases as fm increases, and VB at higher fm is determined by Žå3 ŌĆō (aŽå2)/b. The phase noise floor for SB(fm) is determined by
The comparison of the traditional and proposed phase noise measurement methods from Eqs. (16) to (21) is summarized in Table 1.
It is important that SB(fm) in Eq. (20) does not contain the reference signal phase noise. The SB(fm) in Eq. (20) makes it possible to obtain the SUT phase noise from SB(fm) even if the reference signal phase noise is not sufficiently low or if it is comparable to the SUT phase noise. In such a condition, the variable frequency signal generator with an appropriate phase noise can be chosen for the reference signal instead of a fixed frequency oscillator with an ultra-low phase noise like OCXO. Because the frequency of the reference signal generator can be freely chosen, the factor (a/b) can be made arbitrarily small. Consequently, the measurable phase noise range explained in Section III-1 can be preserved, and the phase noise of the SUT within the measurable phase noise range can be measured. In contrast, in the traditional method, the factor (a/b) is fixed, and the measurable phase noise range may be significantly reduced for a high frequency SUT.
V. Measured Phase Noises
1. Synthesized Signal Generator E8257D
The first SUT is the synthesized signal generator E8257D [24], and its phase noise is measured using the proposed phase noise measurement method. The frequency and power are set to 1.4151 GHz and 5 dBm, respectively. First, the phase noise of E8257D is measured using the signal source analyzer E5052B. The phase noise measured by E5052B at fm = 10 MHz is about ŌłÆ149 dBc/Hz.
The phase noise of E8257D was measured using the proposed phase noise measurement method. The sampling frequency fs = 8 GHz is selected. The phase noise floor is about ŌłÆ136 dBc/Hz, and it will be lowered to about ŌłÆ156 dBc/Hz for M = 10,000 (Fig. 8). Due to higher fs = 8 GHz, the phase noise at lower fm cannot be measured. The minimum offset frequency is set to fm,min = 8 kHz from Eq. (9). The frequency of the reference signal is selected as fref = 2.41 GHz. The reference signal is provided using the synthesized signal generator E4438C [26] from Keysight Technologies. The E4438C phase noise at 2.41 GHz is measured by E5052B, and it is higher by about 5 dB below fm = 1 MHz than the E8257D phase noise. From fref = 2.41 GHz, a/b = Žēd/Žēref = 0.587. The phase noise floor rise is about
10 ŌĆē log 1 + 0.587 2 = 0.64 ŌĆē dB
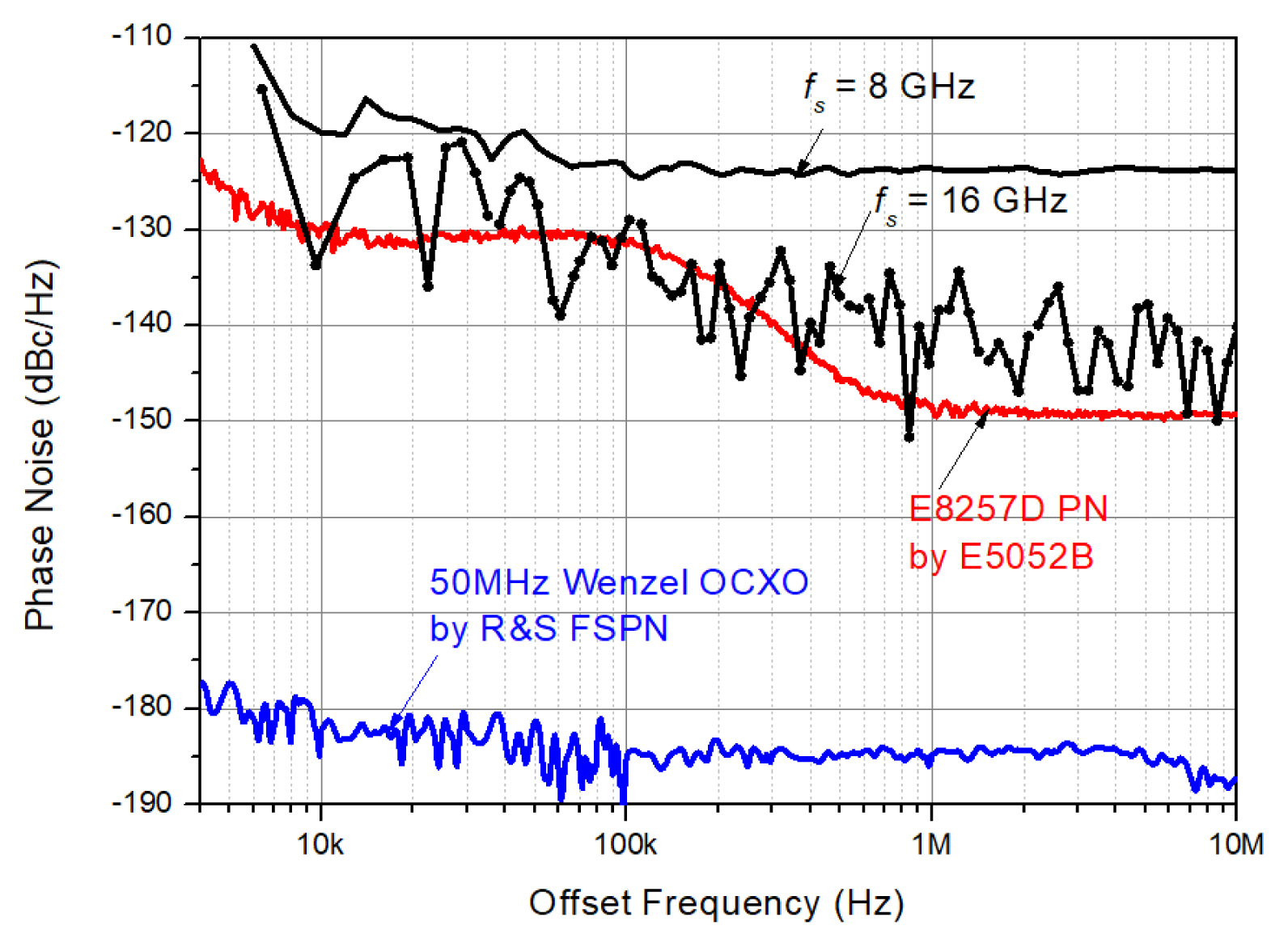
For fs = 8 GHz and fref = 2.41 GHz, the measured phase noise of E8257D for M = 10,000 is compared in Fig. 8, and it shows remarkable agreement with that measured by E5052B. The imaginary part is also shown in Fig. 8, which is about 10 dB lower than the real part. Therefore, the uncorrelated noise is found to be sufficiently attenuated compared with the correlated noises.
To compare the proposed and traditional methods, the phase noise of E8257D is measured again using the traditional method. In the traditional method, the reference signal is the 50 MHz OCXO from Wenzel Associates [25], and its phase noise is shown in Fig. 9. The phase noise of Wenzel OCXO is measured using R&S FSPN, and it is about ŌłÆ184 dBc/Hz at fm = 100 kHz. The measured phase noise for fs = 8 GHz using the traditional method shows a significant gap with that measured by E5052B. Even the measured phase noise for fs = 16 GHz, which is the maximum sampling frequency of MXR608A for the lower phase noise floor, shows a significant gap.
This is because the phase noise floor rise is quite high to measure the phase noise of E8257D. Due to the significant phase noise floor rise, it can be seen that the two-phase noises measured using the traditional methods show a significant gap. For the selected 50 MHz reference signal, the phase noise floor rise and the added reference phase noise between the proposed and traditional methods are compared in Table 2.
From Table 2, the reference phase noise in SA(fm) is ŌłÆ155 dBc/Hz and the reference signal phase noise in SA(fm) can be neglected. However, the phase noise floor rise is 29 dB, and the resulting phase noise floor at fs = 8 GHz and M = 10,000 is about ŌłÆ127 dBc/Hz, which is quite high for measuring the SUT phase noise having a value of about ŌłÆ150 dBc/Hz. Even the improved phase noise floor obtained by altering fs = 16 GHz and M = 10,000 is ŌłÆ130 dBc/Hz, which is still high for measuring the SUT phase noise. Thus, due to the significant phase noise floor rise, the correct value of the SUT phase noise cannot be measured.
From Fig. 9, we can conclude that the correct SUT phase noise cannot be measured using the traditional method when the SUT frequency is higher than the reference signal frequency. A higher SUT frequency generates a higher phase noise floor. Consequently, the measurement of the correct phase noise for a higher-frequency SUT is not possible. It should be noted that the traditional method raises the phase noise floor in the course of the ADC jitter removal. Note that the phase noise floor of the digital oscilloscope is sufficiently low. In contrast, the proposed method almost preserves the phase noise floor of the digital oscilloscope, and the phase noise of E8257D can be successfully measured.
2. Function Generator 33600A
The second SUT is the function generator 33600A [27] from Keysight Technologies. The frequency and power are set to 49.1 MHz and 5 dBm, respectively. This is the case when the SUT frequency is close to the reference signal frequency. The phase noise of 33600A is measured using E5052B (Fig. 10). The phase noise at a frequency offset of 1 MHz is about ŌłÆ146 dBc/Hz.
To measure the phase noise using the proposed method, the sampling frequency fs = 4 GHz is selected. The phase noise floor for M = 10,000 is about ŌłÆ153 dBc/Hz, which is low enough to measure the phase noise of 33600A with ŌłÆ146 dBc/Hz. The signal generator E8257D is used for the reference signal, and its frequency is set to 1.4151 GHz. For the selected reference signal, the phase noise floor rise and the added reference signal phase noise are computed in Table 3. From the table, it can be seen that the phase noise floor rise for the proposed method is negligible. The measured SUT phase noise using the proposed method for M = 10,000 is shown and compared in Fig. 10. The measured phase noise using the proposed method shows remarkable agreement with that measured by E5052B. The imaginary part of this work is shown in Fig. 10, which is about 10 dB lower compared with the real part.
The phase noise of 33600A is measured again using the traditional method. The 50 MHz OCXO from Wenzel Associates is the reference signal for the traditional method. The same sampling frequency fs = 4 GHz as the proposed method is used. For the 50 MHz reference signal, the phase noise floor rise and the added reference signal phase noise are computed and shown in Table 3.
From Table 3, it can be seen that the 50 MHz reference signal adds a negligible reference signal phase noise to SA(fm), and the SUT phase noise can be directly determined from SA(fm). However, the phase noise floor rises by about 3 dB, and the resulting phase noise floor is about ŌłÆ150 dBc/Hz. The phase noise floor ŌłÆ150 dBc/Hz is close to the SUT phase noise ŌłÆ146 dBc/Hz. Fig. 11 shows the measured phase noises using the traditional method for fs = 4 GHz. It can be seen that the measured phase noise using the traditional method shows a close agreement with a lower fm, but it shows the gap at far out fm. The gap of 1.5 dB at a higher fm is due to the phase noise floor rise. Therefore, we can find that the traditional method yields the SUT phase noise close to the correct one for the SUT whose frequency is lower than the reference signal frequency. However, the method shows a significant gap for a higher-frequency SUT.
3. Phase Noise Floor
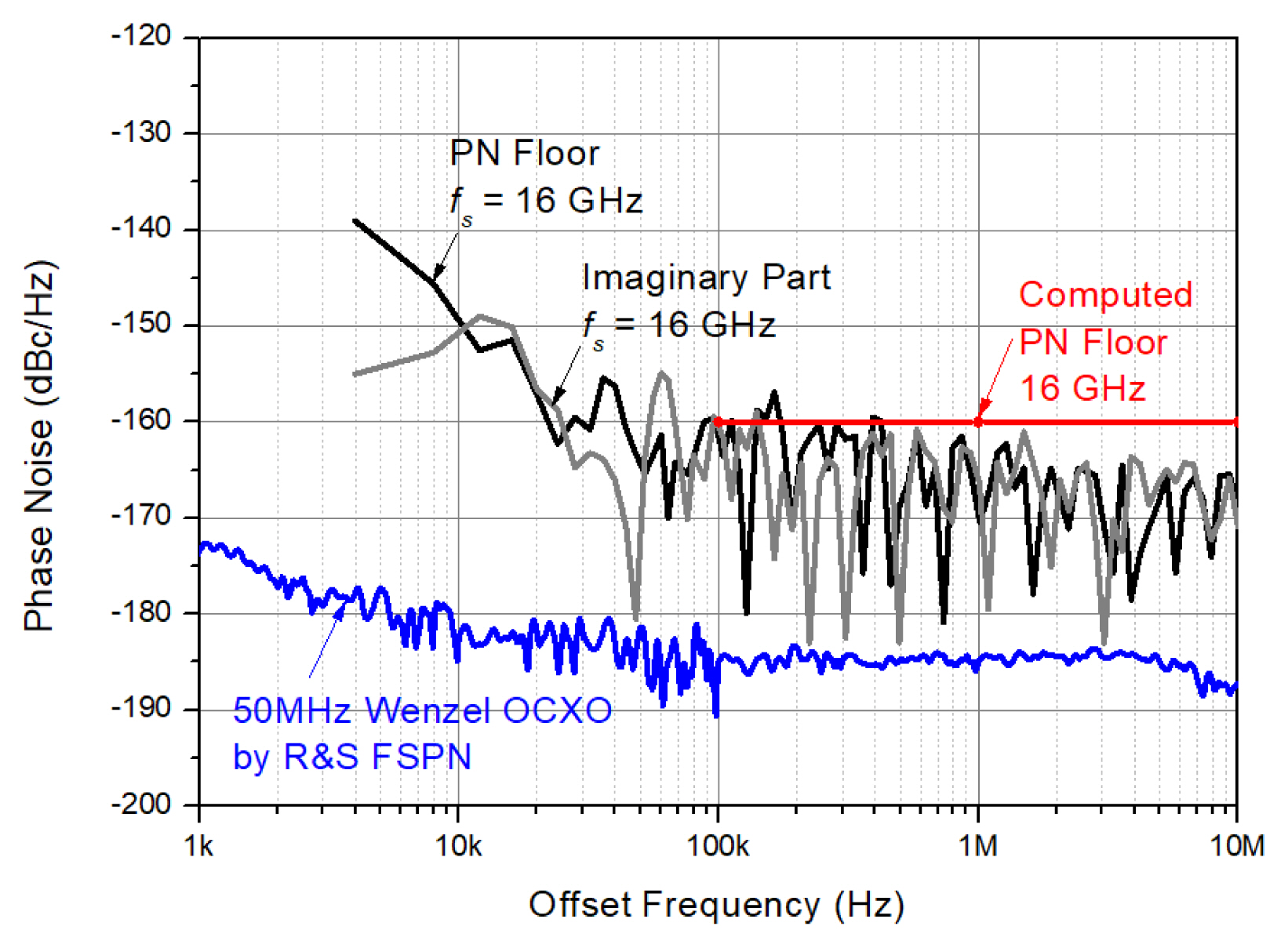
The Wenzel 50 MHz OCXO was selected as the third SUT. The E8257D is used as the reference signal, and its frequency was set to 1.4151 GHz. The phase noise of the Wenzel 50 MHz OCXO is about ŌłÆ180 dBc/Hz as shown in Fig. 9. Therefore, the sampling frequency is set to fs = 16 GHz for the lowest phase noise floor. According to Section III-1, when fs = 16 GHz and M = 10,000, the phase noise floor is estimated to be about ŌłÆ160 dBc/Hz, which is the lowest phase noise floor value.
Taking the phase noise value of about ŌłÆ160 dBc/Hz into consideration, the phase noise of the SUT, the Wenzel 50 MHz OCXO cannot be measured. The measured phase is inferred to show the phase noise floor value of ŌłÆ160 dBc/Hz. The measured phase noise of the Wenzel 50 MHz OCXO is shown in Fig. 12. As expected, it can be seen that it has a phase noise of about ŌłÆ160 dBc/Hz above fm = 100 kHz. The measurement in Fig. 12 provides a way of measuring the phase noise floor value or the sensitivity of the phase noise measurement system. In other words, the system phase noise floor can be alternatively determined by measuring the phase noise of the SUT whose phase noise is below its phase noise floor value instead of the analysis explained in Section III-1. Therefore, the phase noise floor of the phase noise measurement system in this paper is about ŌłÆ160 dBc/Hz.
VI. Conclusion
In this paper, we proposed a phase noise measurement method using a 10-bit digital oscilloscope MXR608A from Keysight Technologies. In addition, we analyzed the ADC phase noise floors and the phase noise due to ADC clock jitter. To evaluate the proposed phase noise measurement method, the phase noises of the synthesized signal generator E8257D and the function generator 33600A from Keysight Technologies were measured. The phase noises measured using the proposed phase noise measurement method were compared with those measured using E5052B. The measured phase noises using the proposed phase shows close agreements with those measured with E5052B.
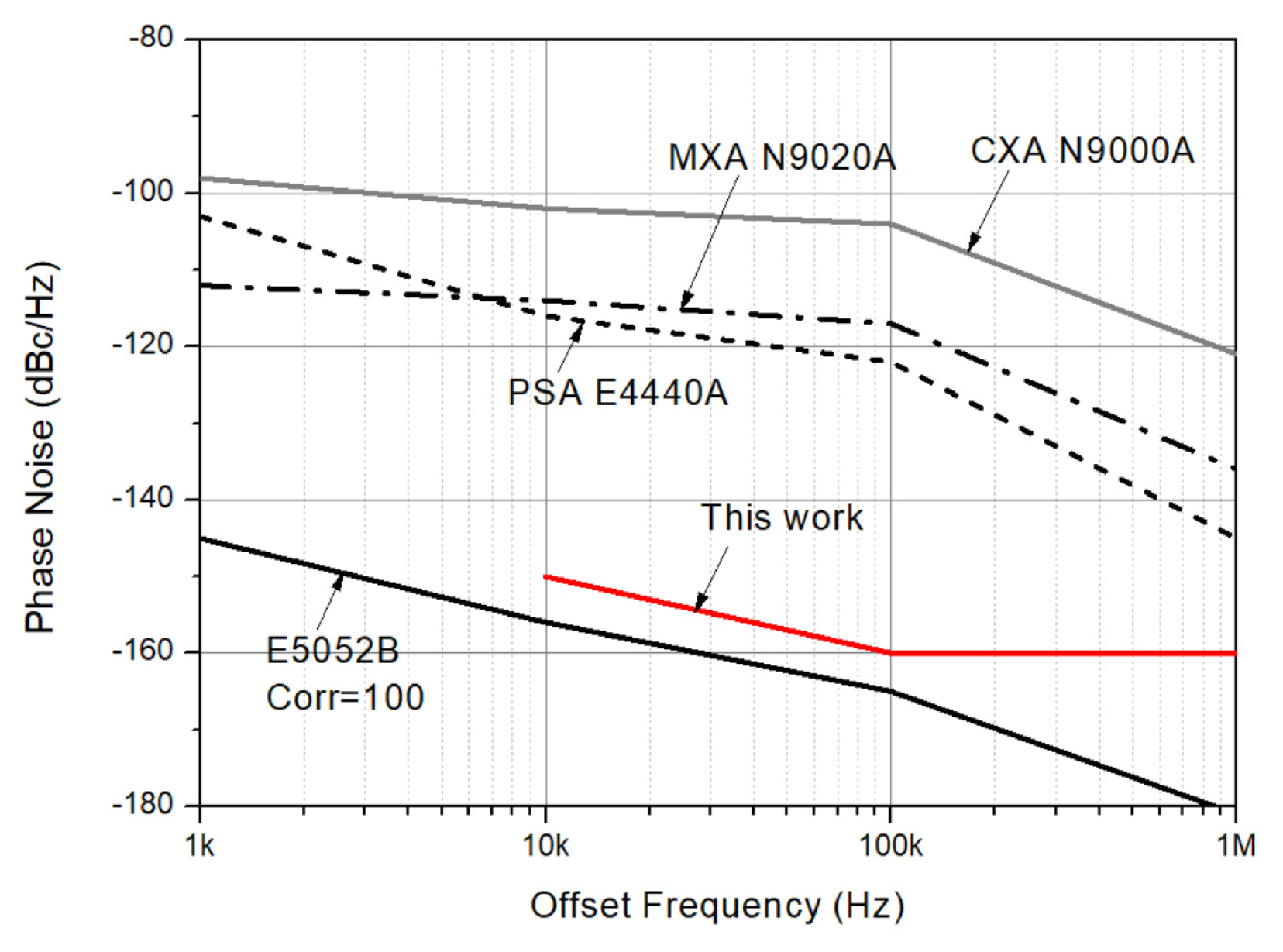
To assess the proposed phase noise measurement method, the phase noise floors of the various general-purpose spectrum analyzers [28] and E5052B for the number of correlation (=100) are shown in Fig. 13. In the case of the spectrum analyzers, typical values instead of specification values were employed to plot. In addition, the phase noise floor of this work was shown for comparison. As shown in Fig. 13, the phase noise floor of this work is far below those of the spectrum analyzers. Therefore, although the phase noise floor of the proposed technique still does not reach that of E5052B, it can be used to measure the phase noise of various SUTs below the phase noise floors of general-purpose spectrum analyzers.
Table 4 compares this work with other works on digital phase noise measurements. Although the number of the ADC bits of this work is smaller compared with other works (phase noise floor degradation of about 20 dB more), the phase noise floor is comparable or better. In particular, the bandwidth is wider than any other works, which is advantageous as a phase noise measurement equipment. We believe that the proposed method is valuable when considering future advances in the number of ADC bits and the bandwidth of digital oscilloscope hardware.