I. Introduction
Ground-penetrating radar (GPR) is a non-destructive electromagnetic system that allows the imaging of subsurface objects. The advantage of GPR is that it senses any kind of material based on variations in its dielectric permittivity and electrical conductivity. As long as the aforementioned responses of buried materials are different from their surroundings, the measured GPR image will contain enough information to distinguish the buried material signature, namely the target, from its surrounding environment [1].
The basic principle of GPR is based on sending and receiving electromagnetic pulses. In one iteration, a 1D signal containing many numbers is obtained, which varies with respect to the dielectric permittivity and electrical conductivity of the penetrated environment. This 1D signal is called an A-scan. When the GPR antenna is used to scan a certain area, many A-scans are collected and concatenated next to each other to construct a 2D signal, which is called the B-scan or the GPR image. Generally, missing data recovery and target detection methods are implemented on GPR images [1].
However, the GPR-based buried target detection concept also faces various challenges. The GPR measurement procedure is highly vulnerable to cases such as difficultly accessing some regions (because of obstacles or other inhibitory factors), highly damaged or corrupted A-scans during data collection, data with clutter that makes buried objects less visible, failures during measurements, or other instrumental problems.
As a result of these issues, partial missing information is a very likely characteristic of GPR measurements [2].
Moreover, missing information leads to poor identification, detection, and analysis of the measured GPR image [3]. Various matrix completion methods have been introduced in the literature, especially in the image processing domain as inpainting methods. They have also been successfully implemented for seismic data recovery issues [3–6]. Generally, these methods are based on interpolation [4], low-rank matrix completion [5], or, more recently, on deep learning-based [6] approaches.
Among these approaches, the low-rank matrix completion-based ones are the most popular. Many techniques have been proposed for low-rank-based matrix completion, such as convex relaxation, gradient, and alternating minimization-based algorithms [7–10]. In one study [7], the available methods were applied to missing information cases in GPR images and a detailed analysis of the various cases was presented. Among the applied methods, the low-rank matrix fitting (LmaFit) [8], nuclear norm minimization (NNM) [9], and non-negative matrix completion (NMC) [10] showed better performance compared to the others and proved their superiority even in extreme cases of missing information in GPR images. Drawing on the above results, this study focused on these three best-performing methods for matrix completion on pixel- and column-wise missing cases with various missing rates.
The region-based convolutional neural network (R-CNN) is one of the most common deep learning architectures used for object detection. Over time, it evolved into Fast R-CNN and Faster R-CNN [11]. The latter integrates a region proposal network (RPN) to produce region proposals directly in the network instead of using an additional algorithm, such as edge boxes. The RPN structure utilizes anchor boxes for object detection. Using region proposals in the network is a faster and better way to converge the loss function with the training data. Because of its model accuracy and end-to-end structure, RPN is used in a wide range of object detection solutions, even in GPR images. Faster R-CNN presents higher accuracy for buried target detection in GPR images, even with a small training dataset [12]. However, in order to implement Faster R-CNN, the GPR image has to be in its proper form (no measurement failures/missing information, as previously discussed). If there are any missing regions in the GPR image because of corrupted A-scans, Faster R-CNN fails to detect the buried target, even if target signature is partially observed. Thus, some pre-processing operations are required for the purpose of presenting a reasonable confidence score for buried object detection.
In this study, we propose a novel framework using cascading matrix completion methods with deep learning-based buried target detection. In our implementation, GPR images with various pixel- and column-wise missing rates are recovered using three different matrix completion methods—LmaFit, NNM, and NMC. After this, the results are fed into the Faster R-CNN for buried target detection purposes. The relation between the matrix completion performance and confidence score of the target detection is analyzed, and both quantitative and visual results are presented.
The rest of this paper is organized as follows: in Section II, the related research on matrix completion approaches is presented. Section III introduces Faster R-CNN-based buried target detection. Section IV is dedicated to explaining the proposed method. In Section V, the visual and quantitative results are presented. Finally, Section VI concludes the paper.
II. GPR Image Recovery
Image recovery methods are extensively applied to image processing problems in different scenarios, such as cases of pixel-wise and column-wise missing information [3]. However, in GPR measurements, column-wise missing cases (missing A-scans) are significantly more common than pixel-wise missing cases. Thus, this study primarily focused on the column-wise missing cases, since they are more challenging. In the experimental results section of this study, two different column-wise and one pixel-wise missing cases are presented.
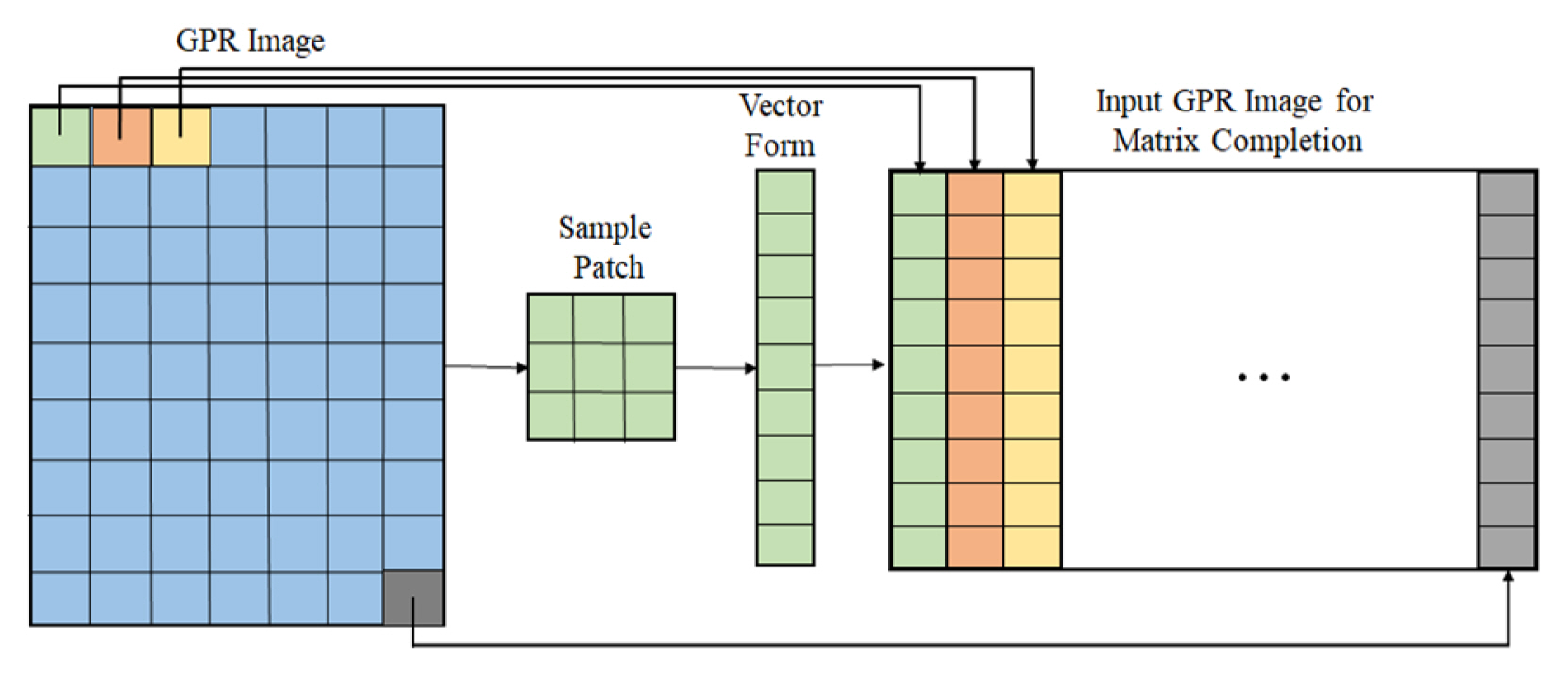
An important step should be followed in the case of column-wise missing information before the implementation of any matrix completion method. According to matrix completion theory, at least one observation for each row and column is necessary [3] (this is not applicable for pixel-wise missing cases). Thus, a pre-transformation step must be applied to the input GPR image with missing information to address this. One study [7] proposed dividing the GPR image into smaller patches, such as 3×3, followed by vectorizing and concatenating them to construct a new input matrix for the GPR image recovery methods, as described in Fig. 1.
Three methods are selected for the matrix completion of the GPR images based on their superior performances [7]—LmaFit [8], NNM [9], and NMC [10]. While each of these methods has its own unique theory, we briefly describe the matrix completion theory in this study. More details on the methods can be found in the literature [8–10].
X ∈ ℝMxN represents the raw GPR image, while Y ∈ ℝMxN denote the GPR image with missing entries in column-wise or pixel-wise cases, respectively. Meanwhile, M and N are the dimensions of X and Y, namely time (ns) and distance (cm) locations. Recovering the exact low-rank matrix can thus be expressed by the following minimization function:
Here, rank(·) denotes the rank of the GPR image X, while Ω stands for an index subset corresponding to the observed entries. i and j are the index values.
We define the projection operator PΩ : ℝMxN → ℝMxN as follows:
Here, PΩ represents the projection on the observation sub-space of the matrices, with non-zero entries constrained to the index subset Ω.
If the GPR image Y is low-rank and its singular vectors are sufficiently spread, the missing locations can be recovered by implementing the following minimization function:
In the above equation, Z denotes an unknown variable matrix, ||. ||F stands for the Frobenius norm, and δ is the tolerance parameter. Furthermore, since the problem in Eq. (3) is NP-hard, it can be relaxed to form a convex optimization problem, expressed as follows:
III. Faster R-CNN-Based Buried Target Detection
The R-CNN, which uses selective search strategies and creates regional proposals for each target image, is one of the most popular object detection models. After constructing the region proposals, features from these proposals are extracted through the CNN architecture. The last step of the R-CNN model is the classification and localization of the target object. After implementing these processes, the target location is presented by the bounding box around it. The introduction of Fast R-CNN adds a new layer—the region of interest (ROI) pooling—which enables the utilization of a single feature map for all proposals extracted using selective search algorithms [11].
ROI pooling solves one of the fundamental problems of fixed image size requirement for object detection observed in previous methods. It can solve recalculating problems resulting from the different sizes of the features. With this new addition to the Fast R-CNN, similar accuracy is obtained with faster training and inference time. However, both R-CNN and Fast-RCNN use selective searches to identify the region proposals. The selective search strategy is a tedious and time-consuming process that has a negative effect on the performance of the network.
In Faster R-CNN, similar to Fast R-CNN, the image is given as an input to a convolutional network that produces a convolutional feature map. However, in Faster R-CNN, instead of using the selective search algorithm on a feature map to define region proposals, it is predicted by a separate network. It is then reshaped by the ROI pooling layer. In the final step, the image within the proposed region is classified to predict the bounding box. As a result, a much faster architecture is obtained compared to its predecessors [11].
1. Training the Faster R-CNN on Simulated GPR Data
CNNs generally consist of convolutional layers, pooling layers, and fully connected layers.
The CNN model in this study includes 3 convolutional layers with dimensions of 16, 32, and 64, with a 5 × 5 kernel size (rectified linear unit [ReLu] is used as the activation function and 2 × 2 maxpooling layer is applied in every convolutional layer). They are fed into one fully connected layer with 64 neurons. The Cifar-10 dataset is selected for pre-training. The simulated GPR images are then used to train the Faster R-CNN, which utilizes pre-trained CNN weights [12].
The simulated dataset is constructed using the gprMax simulation software [13], consisting of 55 simulated GPR images with different burial depths, soil types, object materials, and surface types. This simulated dataset is split as follows: 40 are used for training, 10 are used for validation, and the remaining 5 are used for testing purpose.
IV. Proposed Method
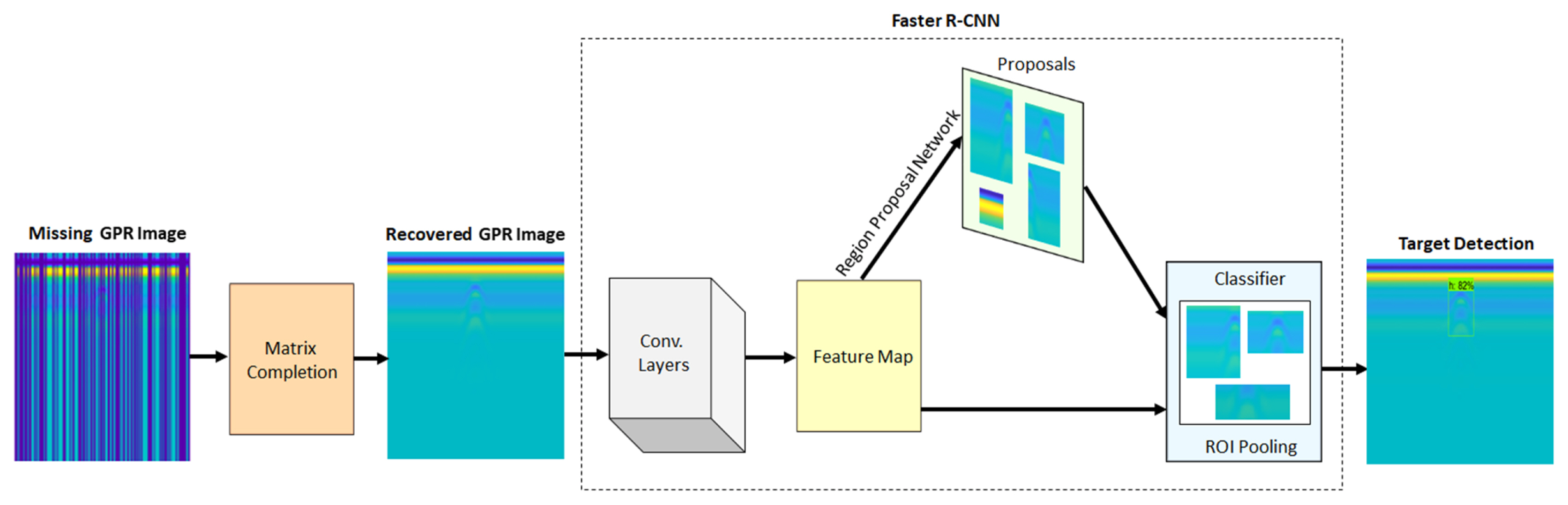
The block diagram of the proposed method, depicted in Fig. 2, is constructed by cascading the methods explained in Sections II and III. First, the GPR image recovery or matrix completion methods (LmaFit [8], NNM [9], and NMC [10]) are applied to the missing GPR image in both the pixel- and column-wise missing cases. The obtained GPR image may contain artifacts over the target region after the recovery process. If the input GPR image in Fig. 2 has no missing information, the matrix completion methods will not have any adverse effect on it (almost the same input GPR image is obtained). Since they are sufficiently fast, applying the matrix completion methods at the beginning of the target detection process does not lead to additional costs for the proposed model.
The recovered GPR image is then fed to the Faster R-CNN network, which is already trained for buried target detection in GPR images (during the training process, GPR images do not contain any missing information). At the end of the network, we obtain the bounding box around the buried target along with its confidence score. The obtained target detection score with Faster R-CNN is directly related to the input of the network, which means the quality of the recovered GPR image (especially the target signature with a hyperbolic shape) via matrix completion algorithms. This indicates that well-recovered GPR images at the input of the network eventually lead to good target detection performances.
V. Experimental Results
In this study, simulated GPR images with missing information for both the pixel- and column-wise cases are used for matrix completion purposes. The Faster R-CNN-based buried target detection model is applied to the recovered GPR images. The simulated data are produced by using the gprMax simulation software [13]. Some of the pixels or A-scans are deleted deliberately for recovery purposes in the obtained simulated data. Since the pixels are deleted manually, the information from the original GPR image is still available for quantitative comparison. Moreover, both visual and quantitative results are analyzed during the comparison. To be more precise, the recovered target signatures are zoomed into in the case of the visual results, and both the peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) are presented in the quantitative comparisons.
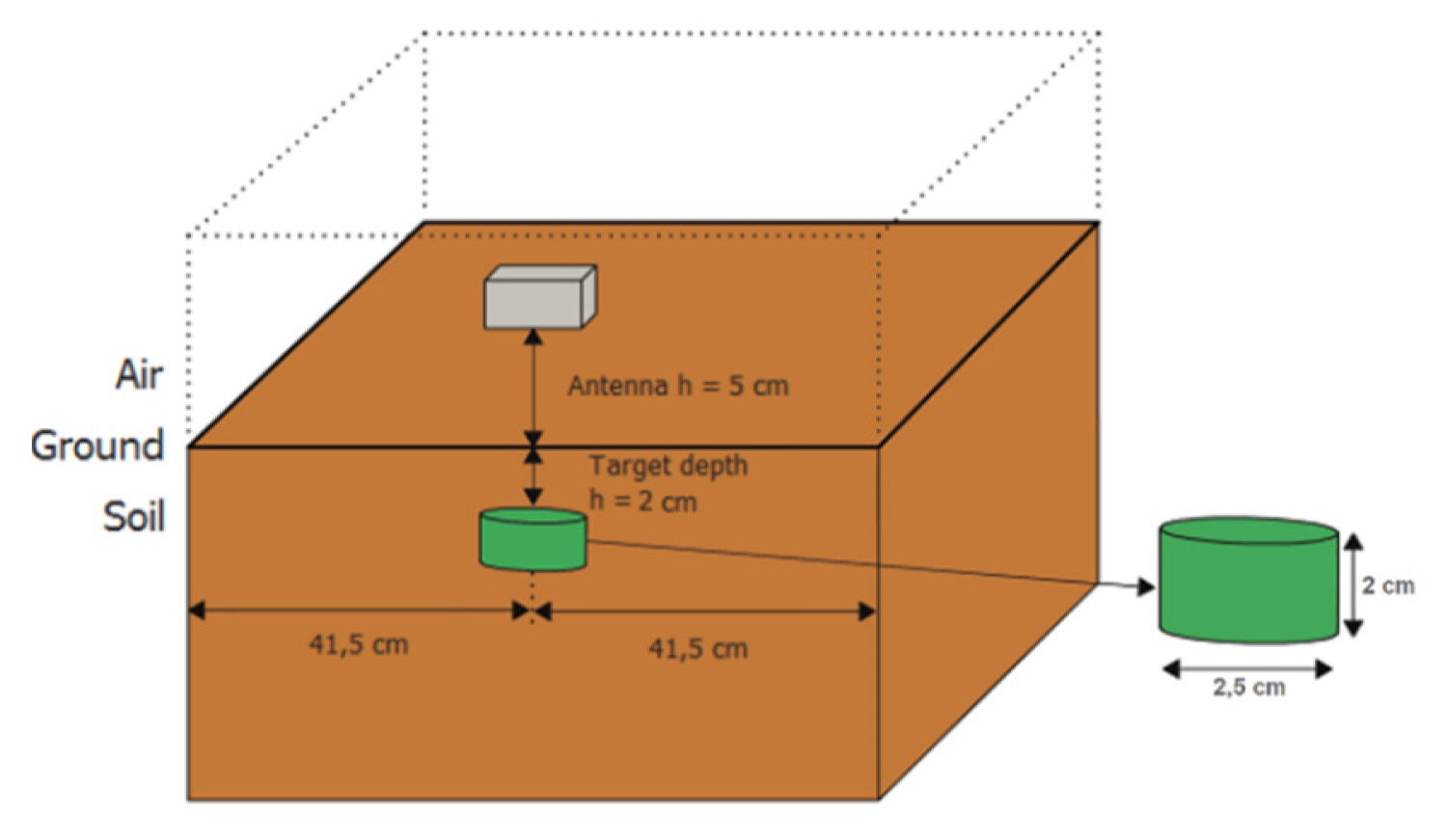
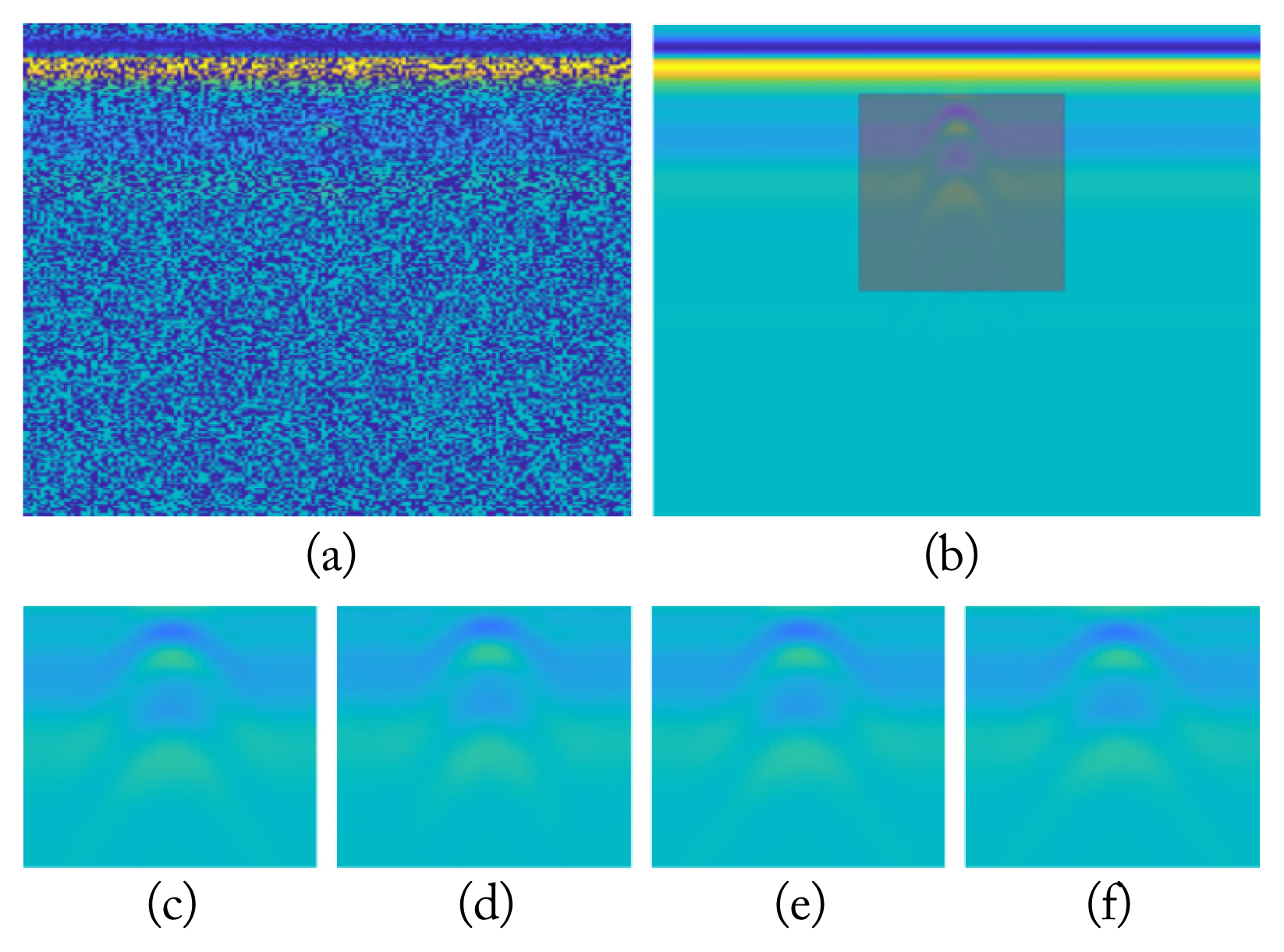
The simulated data are constructed as follows: the buried target is a single aluminum with a dielectric constant (F/m) of 3.1 and conductivity (S/m) of 2.3 × 107. Additionally, the surface and soil types are considered flat and dry sandy soil, respectively, with the latter having a dielectric constant (F/m) of 3.0 and conductivity (S/m) of 0.001. The experimental design of the simulated GPR images is depicted in Fig. 3, which clearly shows the aluminum disk—with dimensions 2.5 cm × 2 cm in radius and height and a burial depth of 2 cm. Antennas are placed 5 cm above the ground and moved 1 cm in each simulation to obtain the A-scan. In each scenario, antennas are moved 80 times to obtain the GPR image; thus, there are 80 A-scans, with each A-scan containing 256 samples. Effectively, the final obtained B-scan or GPR image has a size of 256 × 80. A 1.5-GHz antenna type (Model 5100; Geophysical Survey Systems Inc., Nashua, NH, USA) is selected, which is frequently used in real GPR measurements. The sample simulated GPR image obtained from gprMax is presented in Fig. 4(a). The ideal burial environment (dry sand soil) is selected for the aluminum target (highly reflective). As a result, the target signal can be clearly observed as a hyperbolic structure in the raw GPR image. The target region size is arranged as 70 × 40, as noted in the shaded region in Fig. 5(b).
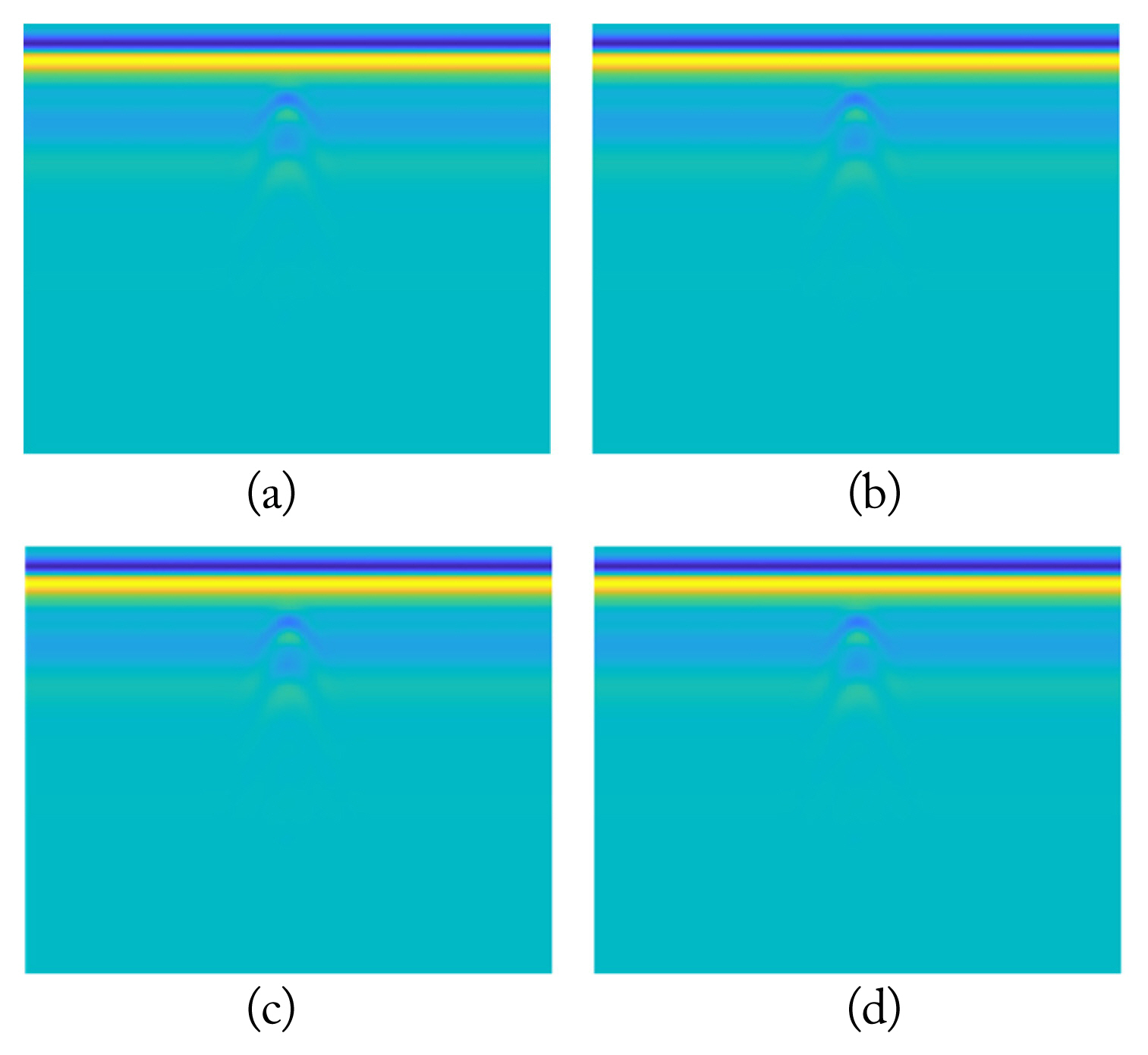
Before the matrix completion results are presented, the effects of the methods are analyzed for cases where the input image has no missing pixels or columns. The outputs of the methods for LmaFit, NNM, and NMC are shown in Fig. 4(b)–4(d). As observed in Fig. 4, if the input GPR image has no missing region, the matrix recovery methods will have no adverse effect on the image. Thus, these methods can be safely used before implementing any target detection algorithm.
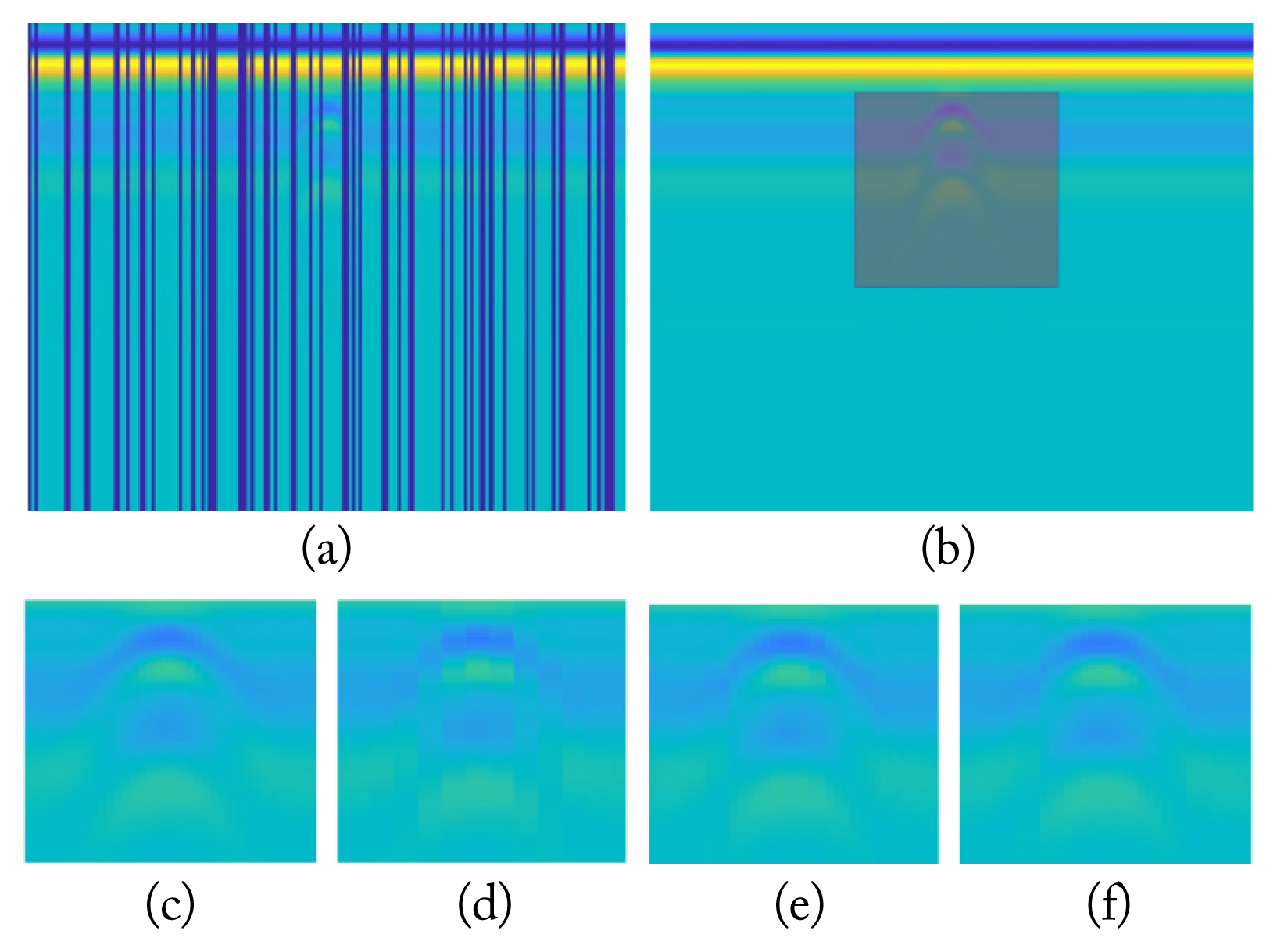
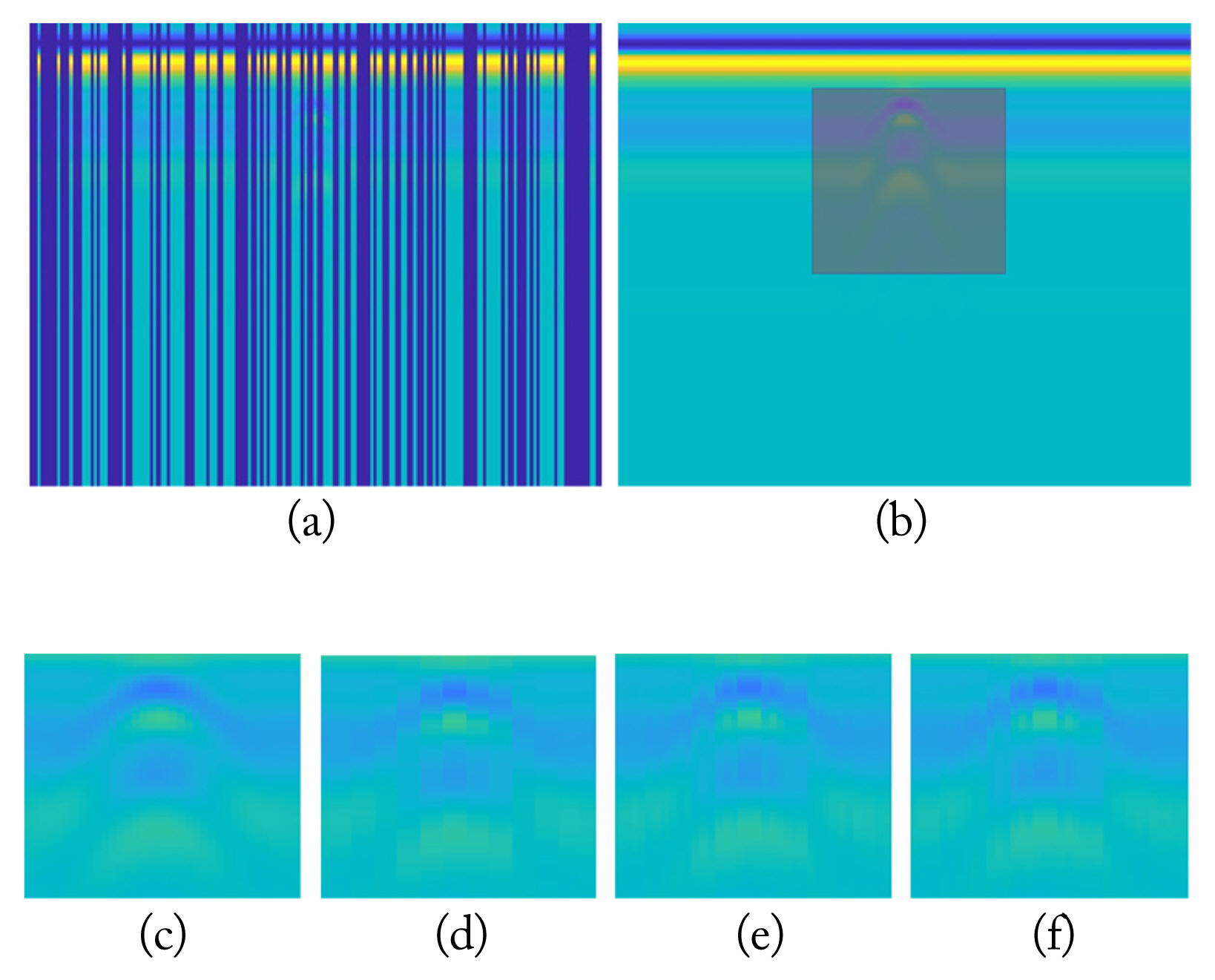
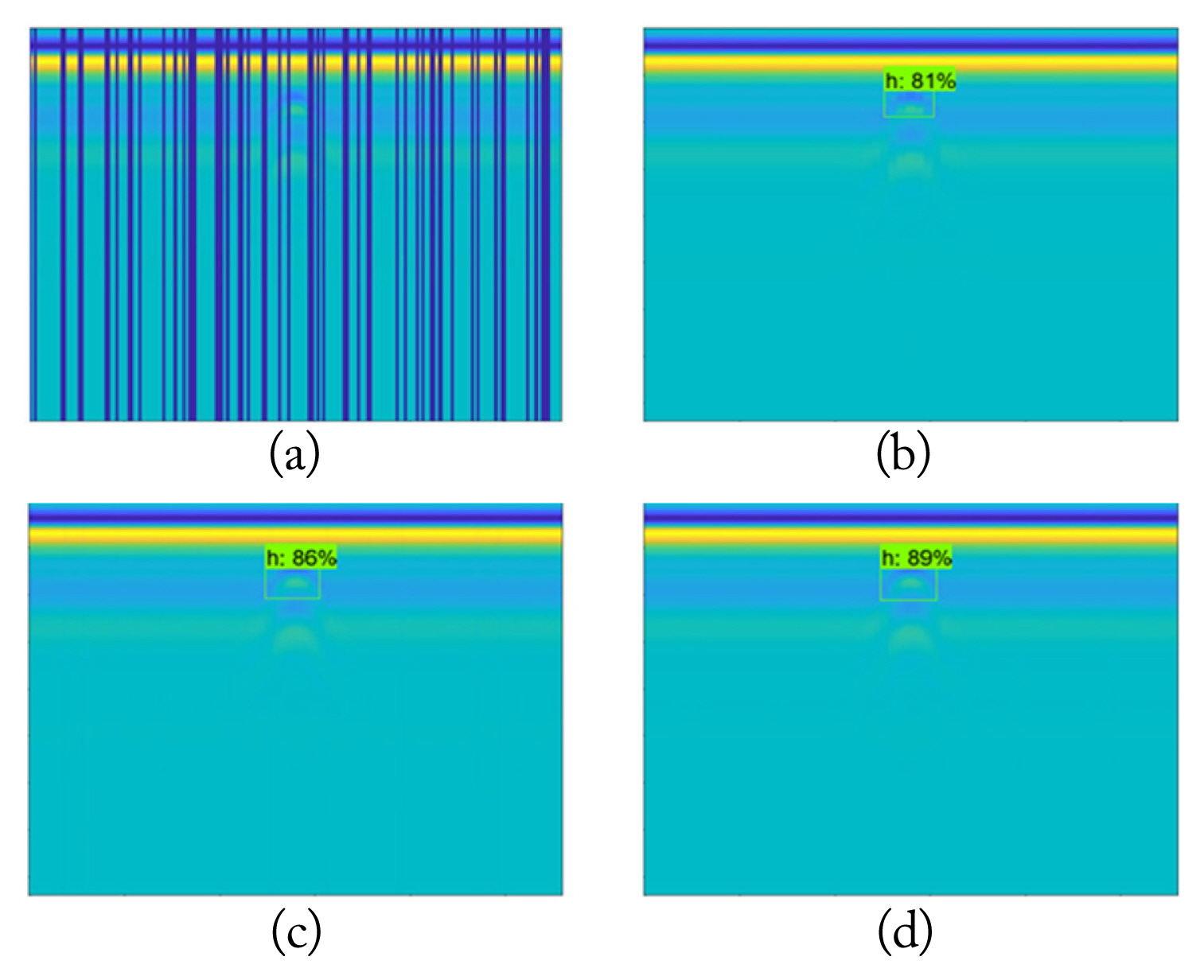
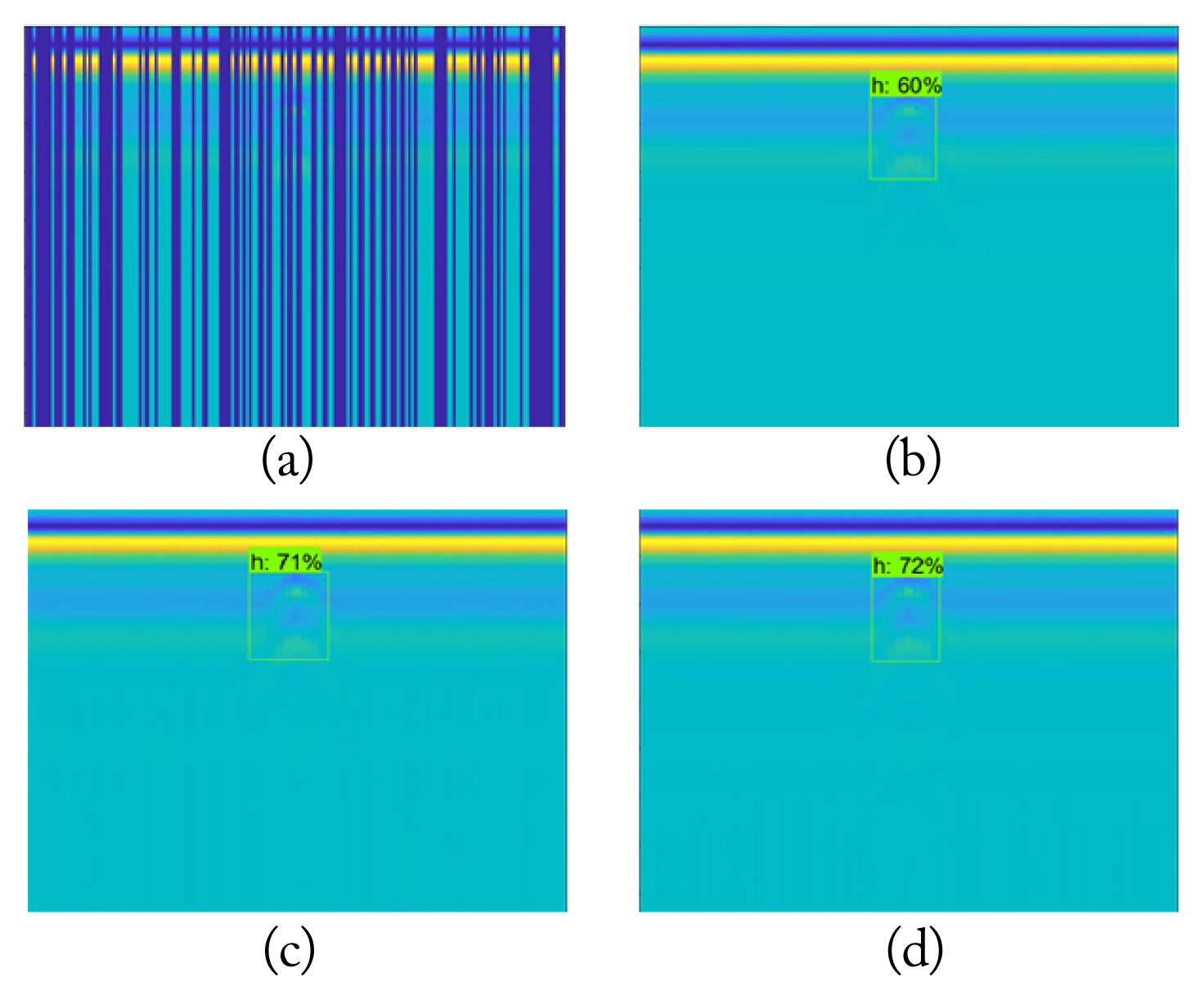
As mentioned before, pixel- and column-wise missing information cases are chosen for matrix recovery methods, wherein the latter is more common and challenging. For the pixel-wise missing information case, the missing rate is arranged as 50%, as presented in Fig. 5(a). The 30% missing rate analysis is skipped for the pixel-wise case since it is a relatively simple case for the matrix completion methods [7]. For the column-wise missing information cases, missing rates are arranged at 30% and 50%, as presented in Fig. 6(a) and Fig. 7(a), respectively. In Fig. 5(a), the target signature is not visible in the missing GPR image, and the target signature is radically corrupted. Furthermore, in Fig. 6(a), the target signature is barely visible. However, in Fig. 7(a), the effects of the missing regions are more severe, while the target signature is also not visible in the missing GPR image.
The simulated raw GPR images in Fig. 4 do not exhibit much variation in the background, with the most significant part of the images being their target signatures, which have a hyperbolic shape. For the visual results of the GPR image recovery methods, the zoomed-in areas for the target signature are presented. To avoid repetition, the GPR image recovery results for the whole GPR image are presented in Figs. 8(b)–8(d), 9(b)–9(d), and 10(b)–10(d). Fig. 5(c)–5(f) present the original and recovered target signatures. As discussed before, the pixel-wise missing case scenario is simpler than the column-wise case. Thus, all the methods recovered the GPR image sufficiently well. It is difficult to identify the performance differences from the visual results for the pixel-wise missing information case. Thus, similar performances are expected from the recovered images in the target detection section.
For the column-wise missing case, two different missing information rates are applied to identify the limitations of the methods. For the 30% missing case, as depicted in Fig. 6(a), the LmaFit presents some blocking effects while the NNM and NMC exhibit better recovery results, as observed in Fig. 6(d)–6(f). For the 50% missing case in Fig. 7(d)–7(f), all the algorithms exhibit a blocking effect. However, LmaFit encounters a more severe blocking effect compared to the others, which is not a desirable characteristic. The NNM and NMC, considering the visual aspect, show similar performances and better recoveries for the target section. However, the NMC is clearly better at recovering the target signature compared to the NNM method, as observed when the recovered signatures are sufficiently zoomed in.
The quantitative results of the pixel-wise missing information case are presented in Tables 2 and 3 for both the target signature and the whole GPR image (as discussed before, the target signature recovery score is significant for the target detection part). Both the SSIM and PSNR scores are used for the detailed quantitative analysis. As seen in Tables 2 and 3, LmaFit obtained better results compared to the NNM and NMC methods. However, all the PSNR scores are quite high—thus satisfying (compared to the column-wise recovery scores) the requirements for the target detection part. We did not expect much variation in the target detection results from the obtained quantitative results for the pixel-wise missing case, since all the values are sufficiently high and can be accepted as a reasonable input for target detection.
The column-wise missing information case results are presented in Tables 4 and 5, where the PSNR scores for the target signature are higher in the 30% missing case and deteriorates in the 50% missing case, where it is far more severe. Thus, increasing the missing information rate causes a degradation in the recovered target signature. When the performance of the methods for the 30% missing case is investigated, it can be observed that the LmaFit has the worst performance among all the methods for both the target signature and the whole GPR image. Notably, the NMC clearly outperforms the NNM, with an approximately 9% better performance in the PSNR. For the 50% missing case, which is quite extreme for the column-wise case, all three methods exhibit very similar performances. However, the NMC again exhibits the best performance for both the target signature and the whole GPR image.
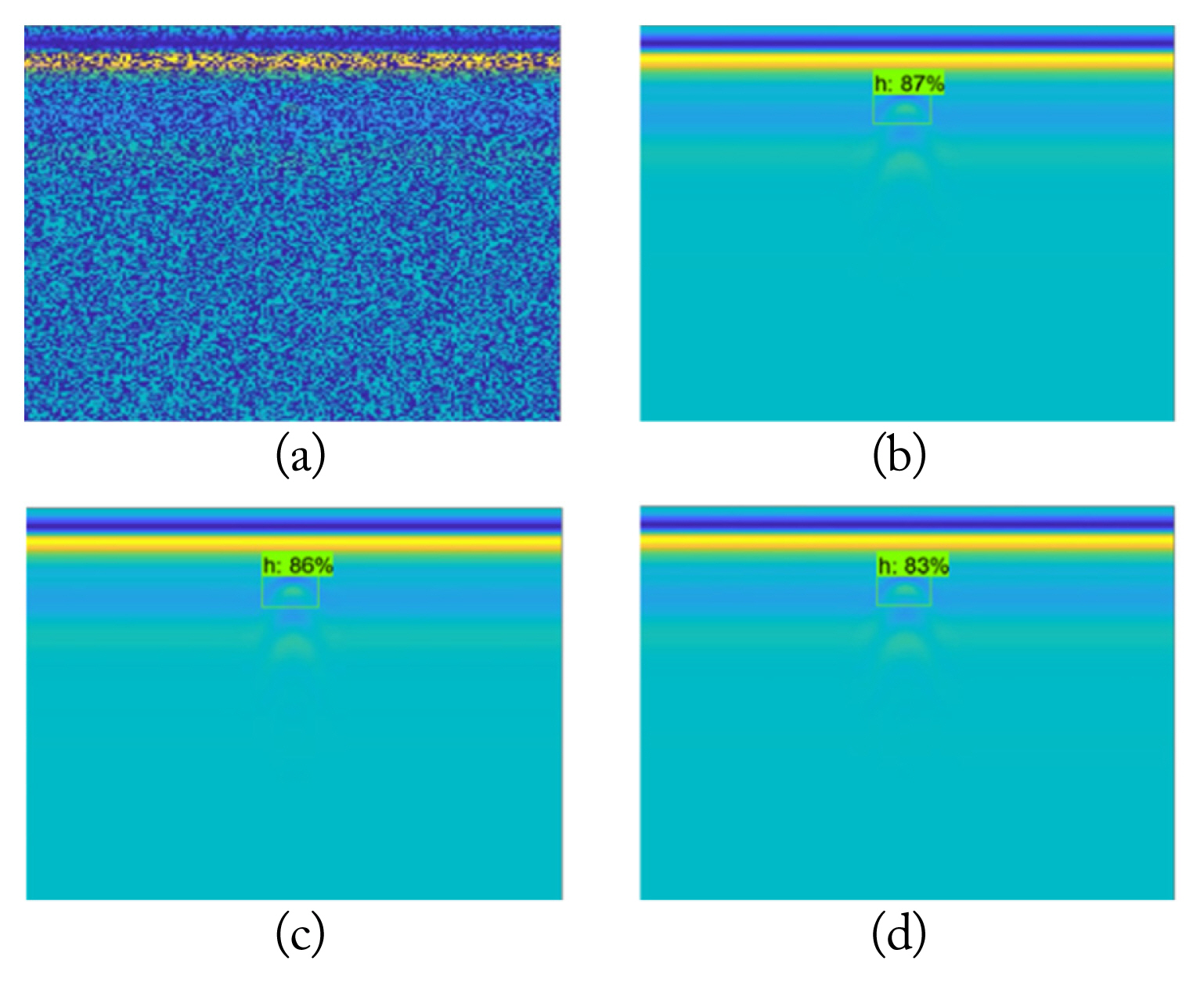
Target detection results based on Faster R-CNN for the 50% pixel-wise missing case are presented in Fig. 8(a)–8(d). As seen in Fig. 8(a), if the GPR image has missing regions, Faster R-CNN fails to detect the target signature (since it is not trained for different missing information cases). However, for the recovered GPR images in Fig. 8(c)–8(d), Faster R-CNN is able to locate the target signature with varying confidence scores, showing very little difference, as expected. All the methods obtained high recovery scores, considering the PSNR for the pixel-wise missing data case. The scores are 87% for LmaFit, 86% for NNM, and 83% for NMC. The comparatively highest and lowest detection scores are obtained by LmaFit and NMC, respectively. As predicted, these results coincide with the recovery results presented in Tables 2 and 3.
Fig. 9(a)–9(d) present the target detection results for the 30% column-wise missing information case. As discussed before, the target is not detected for the missing scenario in Fig. 9(a). For the recovered GPR images in Fig. 9(b)–9(d), the confidence scores are 81% for LmaFit, 86% for NNM, and 89% for NMC. The highest and lowest detection scores are obtained by NMC and LmaFit, respectively. These detection results coincide with the GPR image recovery results presented in Tables 4 and 5.
Fig. 10(a)–10(d) depict the detection results for the extreme case of 50% column-wise missing information. Fig. 10(a) shows that the target is barely visible, indicating that Faster R-CNN cannot detect the target. The LmaFit has the lowest score of 60%, as seen in Fig. 10(b), since the target signature and background contain distortions, which affect the target detection performance. In contrast, the NNM and NMC results in Fig. 10(c) and 10(d) show similar target detection performances of 71% and 72%, respectively.
Notably, the NMC exhibits a slightly better performance than the NNM. As observed in Tables 4 and 5, the NMC also has better recovery results, thus leading to a better detection performance. The results in Tables 4 and 5 and Figs. 9 and 10 prove the strong relation between them and emphasize the importance of cascading for better and more robust target detection results. By comparing the results of the 30% and 50% missing information cases, it can be asserted that higher missing information rates cause degradation of the confidence scores of the detected buried targets under Faster R-CNN.
VI. Conclusion
Three conventional image recovery methods (Lmafit, NNM, and NMC) are applied to missing GPR image scenarios for 50% pixel-wise and 30% and 50% column-wise missing cases. These methods are proposed as pre-processing methods to be implemented prior to any post-processing operations, such as clutter removal or target detection. The experiments reveal that the use of recovery methods does not cause any deterioration even when the original GPR image (that has no missing regions) is considered as the input. On the other hand, if a corrupted GPR image is fed into the Faster R-CNN as input, the buried object cannot be detected. To prove this, both missing and recovered GPR images are fed to the Faster R-CNN-based target detection model. The obtained detection results from the missing and recovered GPR images demonstrate that the target can be detected in the recovered GPR image, while the target in the missing GPR image cannot be detected. The experiments also prove that better recovery leads to better target detection results in GPR.