|
 |
- Search
| J. Electromagn. Eng. Sci > Volume 22(5); 2022 > Article |
|
Abstract
This paper presents a new microwave imaging method using artificial neural networks to localize an object. The trained neural network reconstructs a tomographic image from the measured scattering data, such as a nonlinear electromagnetic inverse scattering solver. The appropriate number of hidden neurons is determined through the cross-entropy between network predictions and target values. To verify this method experimentally, we set up a testbed consisting of 16 antennas that transmit and receive 950 MHz microwaves underwater and used a metal rod with a diameter of 2 mm as a localizing target. The results show excellent imaging performance with fewer artifacts and less than a 2-mm localization error.
Microwave imaging, known as the inverse scattering problem [1], can be widely used in various fields, such as industry, military, medical, and daily life. In particular, with the emergence of the Internet of things, many researchers have recently paid attention to radio frequency (RF) energy rather than light, infrared, and thermal energy when inferring human movement [2]. While visible light cameras are highly sensitive to light and can invade privacy when monitoring humans, RF can pass through nonmetallic materials, unlike light or thermal energy. Because of these advantages, the RF-based localization technique can be used in object tracking, indoor fire detection, survivor sensing, and elderly monitoring. Thus far, many localization technologies have been developed (see Table 1 in [2]). Recently, improved radio tomographic imaging, which reconstructs from the received signal strength, has been presented [3]. The signal patterns induced by the target are different when the target appears at different locations. Therefore, by analyzing the changes in the RF signal, the location of the target can be determined. Other methods include ultra-wideband tomographic radar imaging [4] and multistatic microwave imaging [5]. These methods use the scattering parameters measured. The reconstructed image shows the distribution of the dielectric properties of an object or localizes small anomalies that are stationary or moving [5].
However, there are still challenges to be solved in the nonlinear electromagnetic inverse scattering problem, such as the unpredictability of the scattered signal in a multi-pass environment, the low spatial resolution of the reconstructed image, the uncertainty of the sensor position, and the ill-posedness of inverse problems [1].
On the other hand, an artificial neural network (NN) is recognized as a powerful technique in microwave modeling and design [6]. NNs can learn nonlinear input-output relationships by training with corresponding data. These trained NN models can be used to provide fast answers to learned tasks.
Therefore, NN can also be an efficient tool for developing inverse models for microwave imaging. To this end, this paper presents a new multistatic microwave imaging method that applies NN for object localization under conditions where analytical formulas for inverse models do not exist or are difficult to obtain.
The general configuration of multistatic microwave imaging consists of distributing a certain number of sensors (transmitters and receivers) to a certain region surrounding the object [3ŌĆō5]. Here, the difference in scattering parameters for transmitter n and receiver m, ╬öSm,n, can be obtained by subtracting each scattering data with and without an object:
╬ö S m , n = ŌĆē ŌłŻ S m , n w i t h - S m , n w i t h o u t ŌłŻ
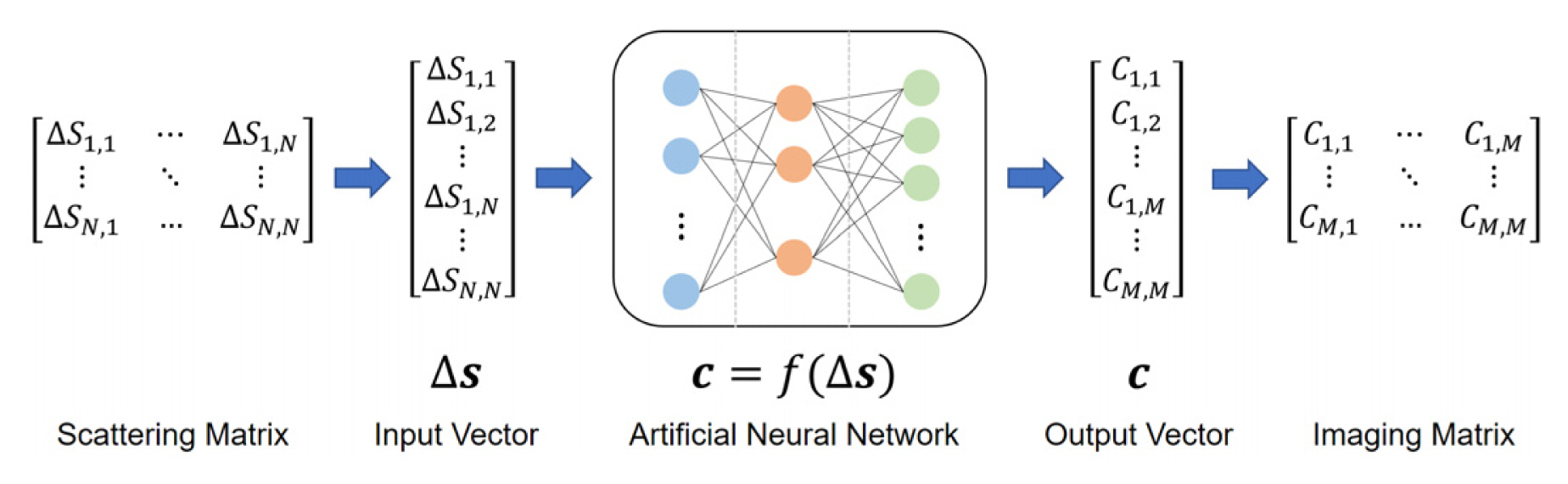
To reconstruct the tomographic image, the scattering data Δs become the input to the NN, as shown in Fig. 1. Then, a nonlinear function f between the input and output can be approximated by NN training: c = f(Δs), where c is reconstructed image data (pixel intensity), meaning the dielectric contrast between the object and the background. Here, the scattering datasets collected from all potential locations are used to train the NN model using supervised learning.
To verify the proposed method, we set up a testbed (Fig. 2). In the water tank (600 mm ├Ś 600 mm ├Ś 400 mm), 16 monopole antennas operating at 950 MHz are arranged with a diameter of 180 mm (the wavelength is about 35 mm in the water). One antenna transmits the microwave signal, and the other antennas receive the propagated signals. This process is repeated sequentially to collect data of 16 ├Ś 16 scattering matrix for the input of the NN. The scattering data are acquired with a vector network analyzer (Keysight E5063A) connected with an in-house-made 2 ├Ś 16 switch matrix (not shown in Fig. 2).
The imaging area is set to 140 mm ├Ś 140 mm. For the reconstruction, the area is divided into 28 ├Ś 28 pixels (5 mm/pixel), which is one-seventh of the wavelength used. Therefore, the number of output nodes of the NN becomes 784. The detailed parameters used in the study are summarized in Table 1. On the other hand, the minimum sampling criteria are reported in terms of the dimension of the reconstruction area and practical measurement aspects (see Section II-B of [4]).
Meanwhile, a metal rod 2 mm in diameter is used for the localizing object. Scattering datasets for 1,000 positions are collected, while the rod is moved to random positions with the XY positioner. Here, 70% of the datasets are used for training, 15% for validation, and 15% for testing.
The well-trained NN expects to convert the measured scattering data into a tomographic image with 5 mm pixels. Then, the image is upsampled to 1 mm pixels by cubic interpolation to obtain a finer image, and the peak is normalized to 1.
In the NN model, the decision of the hidden layer is critical. This is because using too many neurons can lead to overfitting and poor generalization. Therefore, we first investigated how the number of hidden neurons affect localization. The performance, H, was evaluated with the average cross-entropy of N samples used for training:
H ( T , Y ) = - 1 N ╬Ż n = 1 N ╬Ż l = 1 K T n i l o g Y n i
As a result of increasing the number of neurons from 10 to 1,000, cross-entropy was minimized at around 100 neurons and then gradually increased. This shows that increasing the number of neurons does not guarantee performance improvement. The representative results are shown in Fig. 3. Meanwhile, according to the cross-entropy trend, we finally selected 35 neurons in the hidden layer to simplify the NN. The resulting image is almost identical to the image reconstructed with 100 neurons, showing better localization and fewer artifacts.
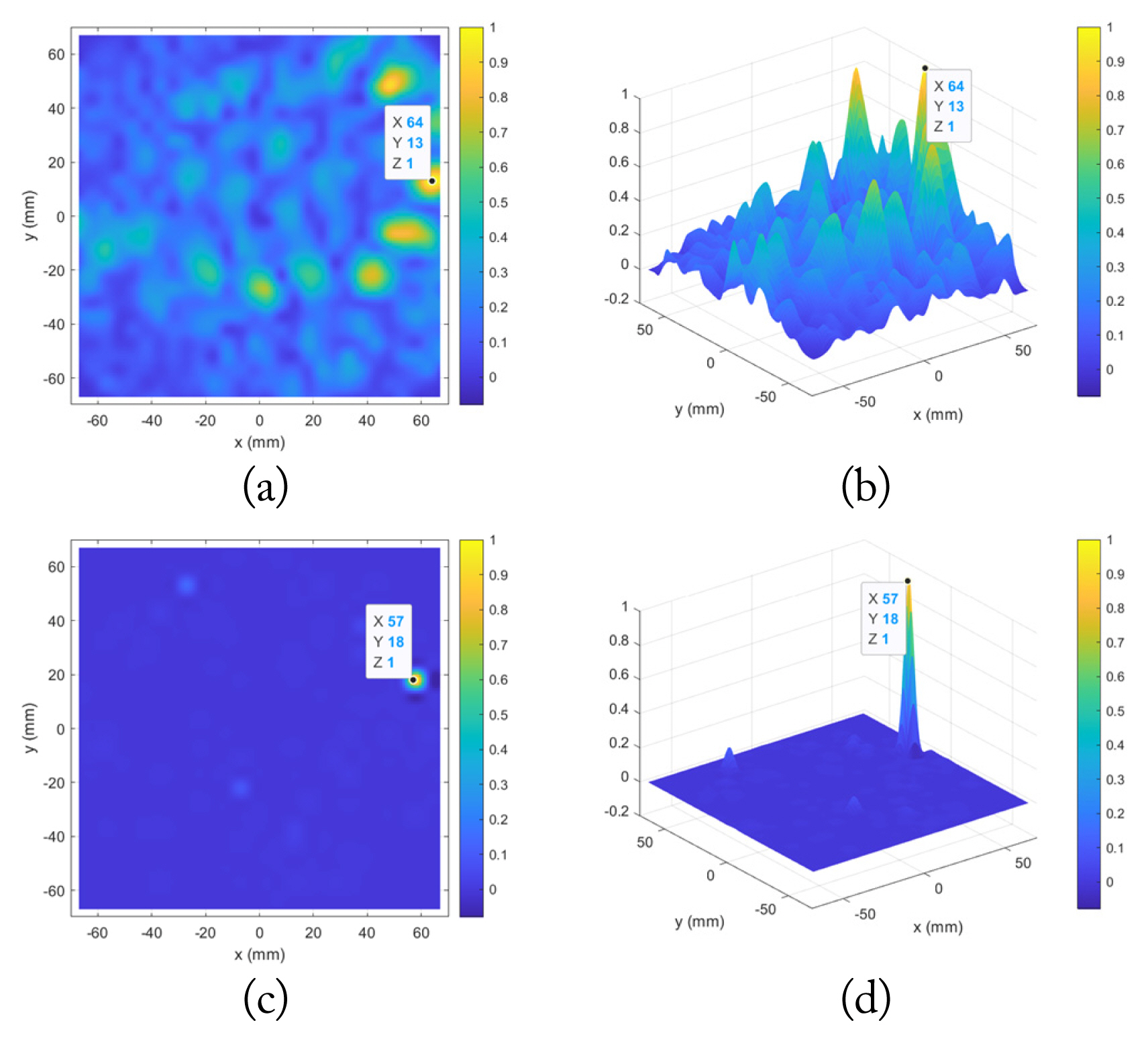
Using the designed NN, we demonstrated two cases. The first is when the position of the object is slightly away from the antenna (Fig. 4), and the second is when the object is close to the antenna (Fig. 5). Here, to show the NN-based method, it was compared with the bi-focusing (BF) method (see Section II-A of [4]), which is one of the conventional imaging methods based on analytical formulation.
Comparing the results in terms of localization error (BF, 4ŌĆō7 mm; NN, 1ŌĆō2 mm), peak-to-sidelobe ratio (BF, 0.7ŌĆō0.9; NN, 0.1ŌĆō0.2), and half-spatial resolution (BF, 15ŌĆō18 mm; NN, 6ŌĆō8 mm), all performances of the proposed NN method are much better.
In this paper, an NN-based microwave imaging method was proposed to localize an object placed under conditions in which it is difficult to obtain an analytical formula. This was verified in an experimental testbed with a 16-antenna array operating at 950 MHz. For this, we designed an NN with 256 inputs and 784 outputs. Here, 35 hidden neurons determined from cross-entropy were used. The trained NN successfully converted the measured scattering data into tomographic image data and localized the object well within a 2-mm error and fewer artifacts, showing excellent imaging performance compared to the conventional method based on an analytical formulation.
Acknowledgments
This work was partly supported by the Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. 2021-0-00731), the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2020R1A2C1A01005221), and the Soonchunhyang University Research Fund.
Fig.┬Ā3
NN-based imaging results according to the number of hidden neurons for an object located at (47, ŌłÆ31) mm.

Fig.┬Ā4
Imaging results for an object located at (ŌłÆ21, ŌłÆ17) mm: (a) 2D and (b) 3D views of BF method, (c) 2D and (d) 3D views of NN method.
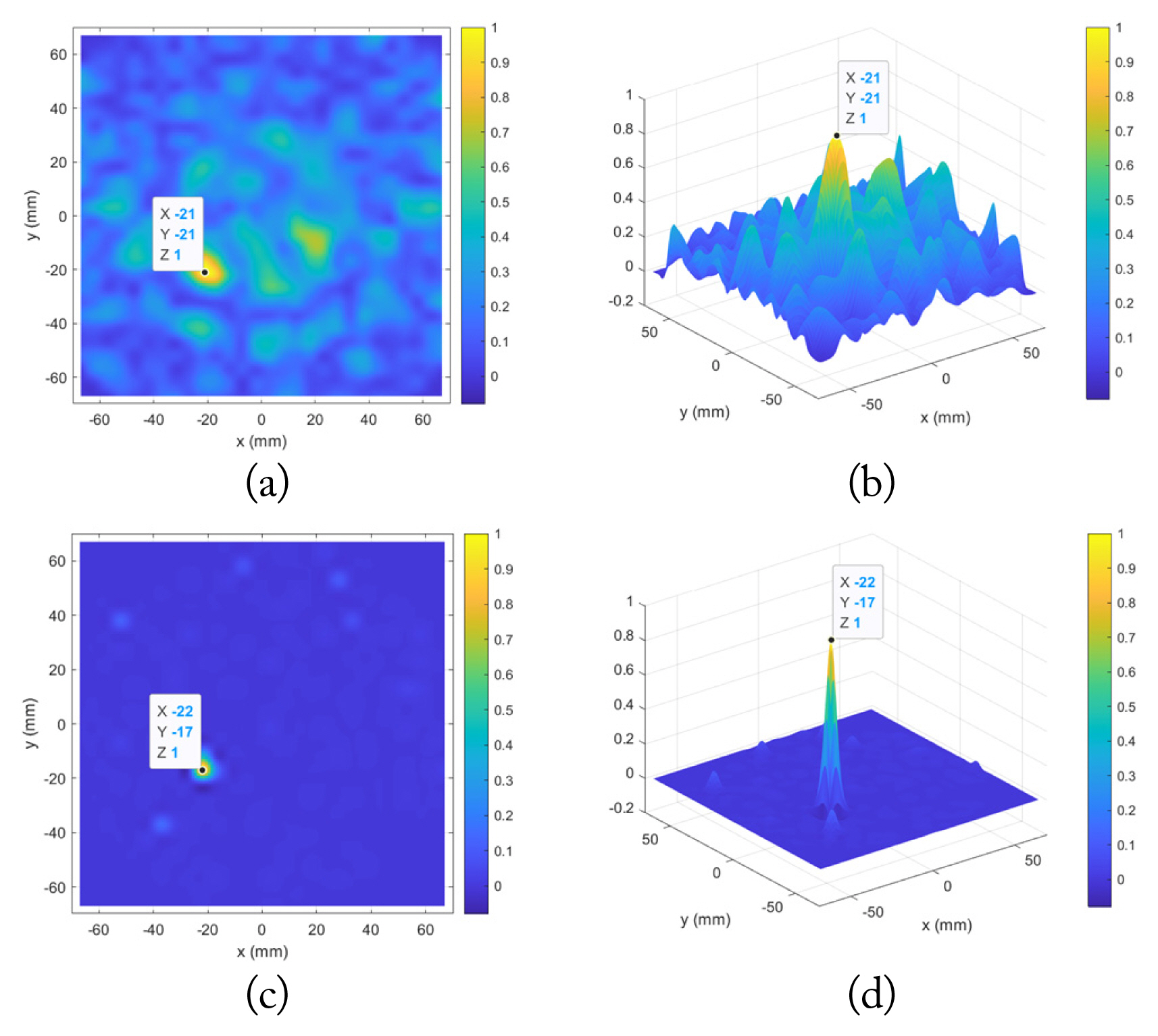
Fig.┬Ā5
Imaging results for an object located at (57, 16) mm: (a) 2D and (b) 3D views of BF method, (c) 2D and (d) 3D views of NN method.
Table┬Ā1
Parameters of the neural network used in this study
References
1. R. C. Aster, B. Borchers, and C. H. Thurber, Parameter Estimation and Inverse Problems. 3rd ed. Cambridge, MA: Elsevier, 2019.
2. H. Obeidat, W. Shuaieb, O. Obeidat, and R. Abd-Alhameed, "A review of indoor localization techniques and wireless technologies," Wireless Personal Communications, vol. 119, no. 1, pp. 289ŌĆō327, 2021.

3. J. Tan, Q. Zhao, X. Guo, X. Zhao, and G. Wang, "Radio tomographic imaging based on low-rank and sparse decomposition," IEEE Access, vol. 7, pp. 50223ŌĆō50231, 2019.

4. L. Jofre, A. Broquetas, J. Romeu, S. Blanch, A. P. Toda, X. Fabregas, and A. Cardama, "UWB tomographic radar imaging of penetrable and impenetrable objects," Proceedings of the IEEE, vol. 97, no. 2, pp. 451ŌĆō464, 2009.

5. W. K. Park, "Application of MUSIC algorithm in real-world microwave imaging of unknown anomalies from scattering matrix," Mechanical Systems and Signal Processing, vol. 153, article no. 107501, 2021.
https://doi.org/10.1016/j.ymssp.2020.107501

6. J. Jin, F. Feng, W. Na, S. Yan, W. Liu, L. Zhu, and Q. J. Zhang, "Recent advances in neural network-based inverse modeling techniques for microwave applications," International Journal of Numerical Modelling: Electronic Networks, Devices and Fields, vol. 33, no. 6, article no. e2732, 2020.
https://doi.org/10.1002/jnm.2732

Biography

Wonhyung Son received the B.S. degree in mechanical engineering from Soonchunhyang University, Asan, South Korea, in 2020, and the M.S. degree in ICT Convergence from the same university, in 2022. He is currently working as a researcher at DMTS Co. (Daejeon R&D Lab), Ulsan, Korea. His research interests include electromagnetic/mechanical wave sensing and imaging, machine learning, and mechatronics.
Biography

Won-Kwang Park received the M.S. degree in mathematics from Yonsei University, Seoul, South Korea, in 2004, and the Ph.D. degree in applied mathematics from the Ecole Polytechnique, Palaiseau, France, in 2009. After graduation, he joined the Institute for Mathematics and Scientific Computing, Karl Franzens University of Graz, Austria, as a Postdoctoral Researcher, in 2009. In 2010, he joined the Department of Mathematics in Kookmin University, as a full-time lecturer, where he is currently a full professor at the Department of Information Security, Cryptology, and Mathematics in Kookmin University. His research interests include inverse problems, microwave imaging, and scientific computing.
Biography

Seong-Ho Son received the B.S. degree in control and mechanical engineering from Pusan National University, Busan, South Korea, in 1997, and the M.S. and Ph.D. degrees from Pohang University of Science and Technology (POSTECH), Pohang, South Korea, in 1999 and 2009, respectively. From 1999 to 2001, he was a researcher with the Technical Research Center, Daewoo Motors (now, GM Korea), Incheon, South Korea. From 2001 to 2019, he was a principal researcher with the Radio and Satellite Research Division, Electronics and Telecommunications Research Institute (ETRI), Daejeon, South Korea, where he was involved in the development of microwave medical imaging and thermotherapy technologies. Since 2019, he has been an assistant professor with the Department of Mechanical Engineering, Soonchunhyang University, Asan, South Korea, where he also joined the Department of ICT Convergence. His research interests include electromagnetic/mechanical wave sensing and imaging, phased arrays, mechatronic systems, and machine learning.
- TOOLS
-
METRICS

-
- 1 Crossref
- 0 Scopus
- 1,636 View
- 68 Download
- Related articles in JEES
-
A Simple Microwave Backscattering Model for Vegetation Canopies2005 ;5(4)