I. Introduction
Typically, several power and signal lines are installed in offshore plants. Electromagnetic fields (EMFs) produced by high-voltage power lines can affect living organisms; therefore, a guide for determining a safe distance has been suggested [
1].
These EMFs generated from the power lines can also affect other cables, resulting in interference among cables, which is referred to as called crosstalk [
2]. The shielding characteristics of a cable tray have been extensively studied so far [
3].
S-parameters were obtained through modeling and simulation, and experiments were conducted to determine the differences in shielding effectiveness (SE) based on the width-to-height ratios of U-shaped cable trays, which are commonly used in the industry [
3].
The holes in a cable tray make it easy to attach cables or other fixings. In addition, they can reduce the tray’s weight and enable drainage and ventilation. However, an increased area of holes can cause interference between cables. To minimize crosstalk between cables, holes are designed to have an optimal geometry. In this study, the SE of various shapes and numbers of holes in cable trays were compared through simulations and experiments. Using the analysis results, an algorithm was proposed to determine the optimal geometry of holes in the cable tray for the desired area of holes.
The rest of this paper is organized as follows. The algorithm proposed to find the optimal geometry is presented and validated in Section II. The conclusions are presented in Section III.
II. Proposed Algorithm to Find Optimal Geometry
This paper proposes an efficient algorithm to determine the optimal geometry of holes in the cable tray for the desired area of holes. The detailed process of the proposed algorithm is described in this section.
1. Dataset Collection
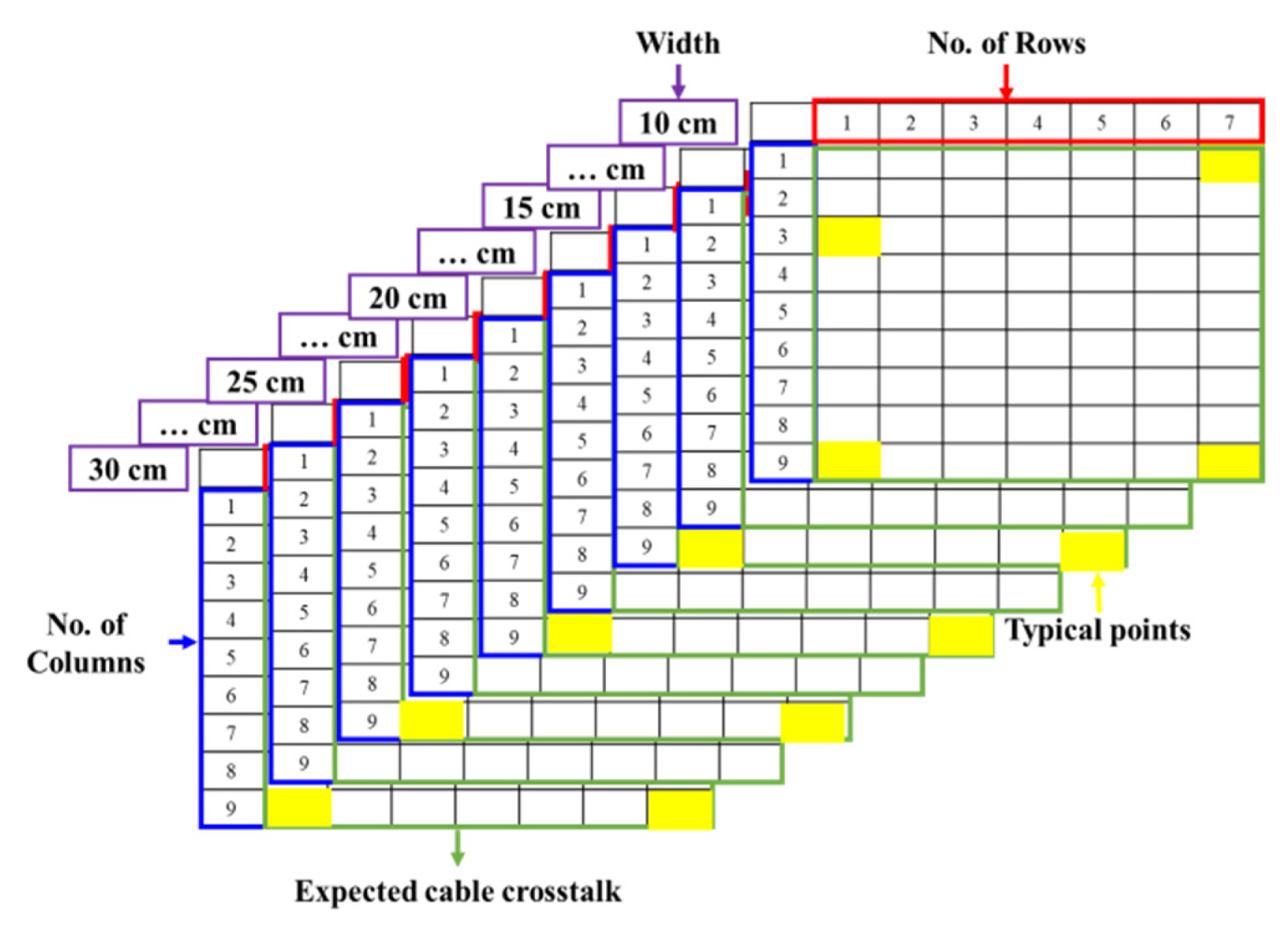
To construct a dataset for training the relationship between the hole geometry in the cable tray and cable crosstalk, the input and output variables of the dataset must be defined. We chose width, number of columns, and number of rows of holes as the input variables. The hole height was fixed at 100 mm because it had no significant effect on the cable crosstalk. The range of variables is listed in
Table 1, and the number of datasets was 1,323.
To construct a database, the simulation results of the crosstalk analysis performed with High Frequency Simulation Software (HFSS) were used. The S-parameter of near-end coupling (S21) had different values depending on the frequency. In addition, S21 exhibited a similar tendency in the simulations. Instead of using all S21 values at all frequencies, the representative value was used as the output value of S21 for the proposed algorithm. S21 at the 1 MHz frequency is one of the values with similar tendency. Therefore, the difference in S21 between cable trays with and without holes at the 1 MHz frequency was used as the output value of the dataset.
The low output value of
S21 indicates a high SE. As shown in
Fig. 1, the expected values of crosstalk at the rest point between two typical points can be obtained using the crosstalk simulation results at the typical points.
2. Training Dataset using Neural Network
The dataset was trained using a neural network. The network had three inputs, 10 hidden layers, and one output and was trained using the Levenberg–Marquardt backpropagation method. This method is generally used for addressing data optimization problems [
4]. For training, validation, and testing, the dataset was divided into three parts: 70% for training, 15% for validation, and 15% for testing.
3. Finding Optimal Hole Geometry Using Neural Network
In our proposed algorithm, when we enter the value of the desired area of the holes in the cable tray as input, the optimal geometry of holes with minimum expected crosstalk is suggested based on a trained neural network. The detailed algorithm is presented as follows:
Step 1: Input the desired area of holes and output possible cases of geometry with width, height, number of columns, and number of rows of holes.
Step 2: Output the predicted crosstalk based on the neural network by using possible cases of geometry obtained from the results of Step 1. The possible cases indicate possible hole geometries in the cable tray for the desired area.
Step 3: Find the hole geometry with minimum expected crosstalk from the results of Step 2.
4. Experiments and Discussion
We performed experiments to evaluate the performance of the proposed algorithm and to determine the optimal geometry of the holes in the cable tray. All approaches mentioned in this section were programmed using MATLAB. The training and testing processes were performed on a PC with an Intel i5-9400F processor, 32 GB RAM, and a clock rate of 2.9 GHz using the Windows 10 operating system (64 bit).
For example, to design holes in cable trays with 84,000 mm
2 area, we used an 84,000 mm
2 area as input and then obtained the optimal hole geometry as the output using the proposed algorithm. As shown
Table 2, when an 84,000 mm
2 area of holes is used as the input, we can obtain the possible cases of various hole geometries, including the optimal geometry of holes.
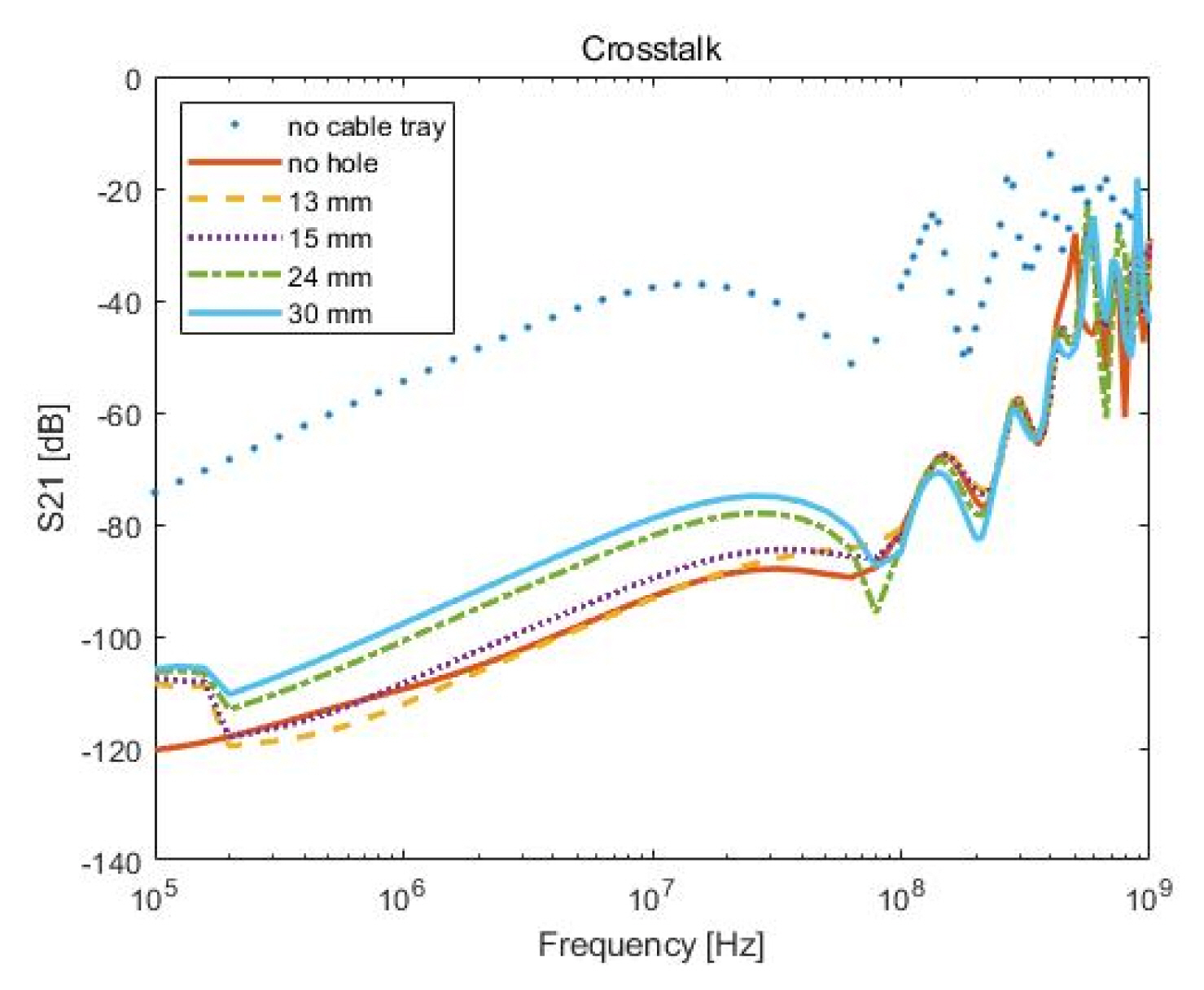
To verify the experimental results obtained using the proposed algorithm to determine the optimal hole geometry, a simulation was performed using HFSS.
As shown in
Fig. 2, the simulations were performed by varying the hole height as 13, 15, 24, and 30 mm while maintaining the width at 100 mm. Moreover, the number of holes was set as 9 × 7/8 × 7/5 × 7/4 × 7 to maintain the total hole area.
As shown in
Fig. 3, the simulation results were similar to those obtained using the proposed algorithm to find the optimal hole geometry using a neural network.
III. Conclusion
The SE of cable trays used in offshore plants was analyzed for cable trays with and without holes through simulations and experiments. The SE of the parallel holes was verified by varying the width and length of the holes. Using the analysis results, an algorithm was proposed to determine the optimal geometry of holes in the cable tray and was verified through simulations. These results can be useful for the designers of cable trays with holes.