Novel Parameter Estimation Method for a Ballistic Warhead with Micromotion
Article information
Abstract
This paper proposes a novel method to estimate the parameters of a ballistic warhead with micromotion. First, the independent component analysis decomposes the echo signals received from the ballistic warhead into individual signals corresponding to each scatterer. Second, the one-dimensional micro-Doppler frequency trajectories are extracted from two-dimensional joint time-frequency images of decomposed individual signals. Finally, the adaptive particle swarm optimization is used to estimate the parameters that best match the mathematical model composed of unknown parameters to the one-dimensional micro-Doppler frequency trajectories. In simulations using a conical warhead model, the parameters for a ballistic warhead with micromotion are accurately estimated.
I. Introduction
A ballistic missile is a great threat in the modern battlefield because of its high maneuvering speed and low radar cross-section (RCS). Specifically, it releases a decoy to avoid the detection of the warhead by radar. Therefore, it is necessary to discriminate the warhead from the decoy. However, conventional methods based on the range profile and the inverse synthetic aperture image in [1] and [2] have limited ability to discriminate them because of the similarity in shape and the overall trajectory of the warhead and the decoy. The problems of existing methods can be overcome by exploitingthe difference in their micro-Doppler (MD) effect [3–8]; the warhead is much heavier due to various devices, and thus its micromotion is different from that of the decoy. The parameter estimation for a ballistic warhead with micromotion can be utilized to solve the problem of discrimination between warhead and decoy. However, this inevitably requires both signal decomposition and data association because of the simultaneous appearance of individual signals corresponding to the multiple scatterers of a ballistic warhead. In addition, the estimation of several parameters makes the optimization task quite difficult.
To solve this problem, many studies have been carried out on parameter estimation based on two trajectories: the high-reolution range profile (HRRP) trajectory in [9–12] and the MD frequency trajectory in [13, 14]. Parameter estimation can be achieved using HRRP trajectories for the multiple scatterers of a ballistic warhead with micromotion. For example, HRRP trajectories can be obtained using both the theory of sparse representation in [9] and the dynamic programming in [10] for parameter estimation. Luo et al. [11] proposed the parameter estimation framework using HRRP trajectories in distributed radar networks. Hong et al. [12] developed a factorization-based approach with sparse representation. However, the conventional methods in [9–12] require a large bandwidth to obtain HRRP trajectories from a high-quality two-dimensional (2D) range-time map, leading to inefficiency in terms of radar resources. Alternatively, the MD frequency trajectories can be utilized to estimate the parameters for a ballistic warhead with micromotion despite the small bandwidth. For example, Li and Varshney [13] used a parametric sparse representation to focus on the decomposition of echo signals received from multiple scatterers and the estimation of their parameters. Zhou et al. [14] used a modified general parameterized time-frequency transform to increase the accuracy of signal decomposition. However, the methods in [13] and [14] require a complex image processing procedure to decompose the MD frequency trajectories from a high-quality 2D joint time-frequency (JTF) image, resulting in a considerable computational time. The problem of signal decomposition can be solved by the independent component analysis (ICA) technique in [15]. Nevertheless, the drawback in terms of robustness against noise still exists in [15] because MD frequency trajectories are extracted to take the time derivative of the phase term of decomposed individual signals. Therefore, a new framework based on the MD frequency trajectories is required for an efficient and robust parameter estimation for a ballistic warhead with micromotion.
In this paper, we suggest a novel framework to estimate the parameters of a conical ballistic warhead with micromotion. First, we assume that a phased array antenna with M elements observes a conical target composed of N scatterers (N < M) with micromotion (e.g., coning and nutation). Second, the ICA decomposes M one-dimensional (1D) time domain complex echo signals into N individual signals corresponding to each scatterer by exploiting their statistically independent nature [16, 17]. Third, the 1D MD frequency trajectories are extracted by selecting a Doppler frequency of a maximum peak along the time direction in the 2D JTF image of the decomposed individual signals. Finally, the parameters that best match the mathematical model composed of unknown parameters to the 1D MD frequency trajectories are estimated using the adaptive particle swarm optimization (APSO), which is the elitist learning strategy based on the evolutionary state estimation approach [18]. In simulations using a computer-aided design (CAD) model for a conical target and a commercial numerical electromagnetic solver VIRAF, which is a commercial numerical electromagnetic solver based on both physical optics and the physical theory of diffraction, the proposed method successfully estimates the parameters for a ballistic warhead with micromotion.
II. Modeling and the Proposed Method
1. Signal Model
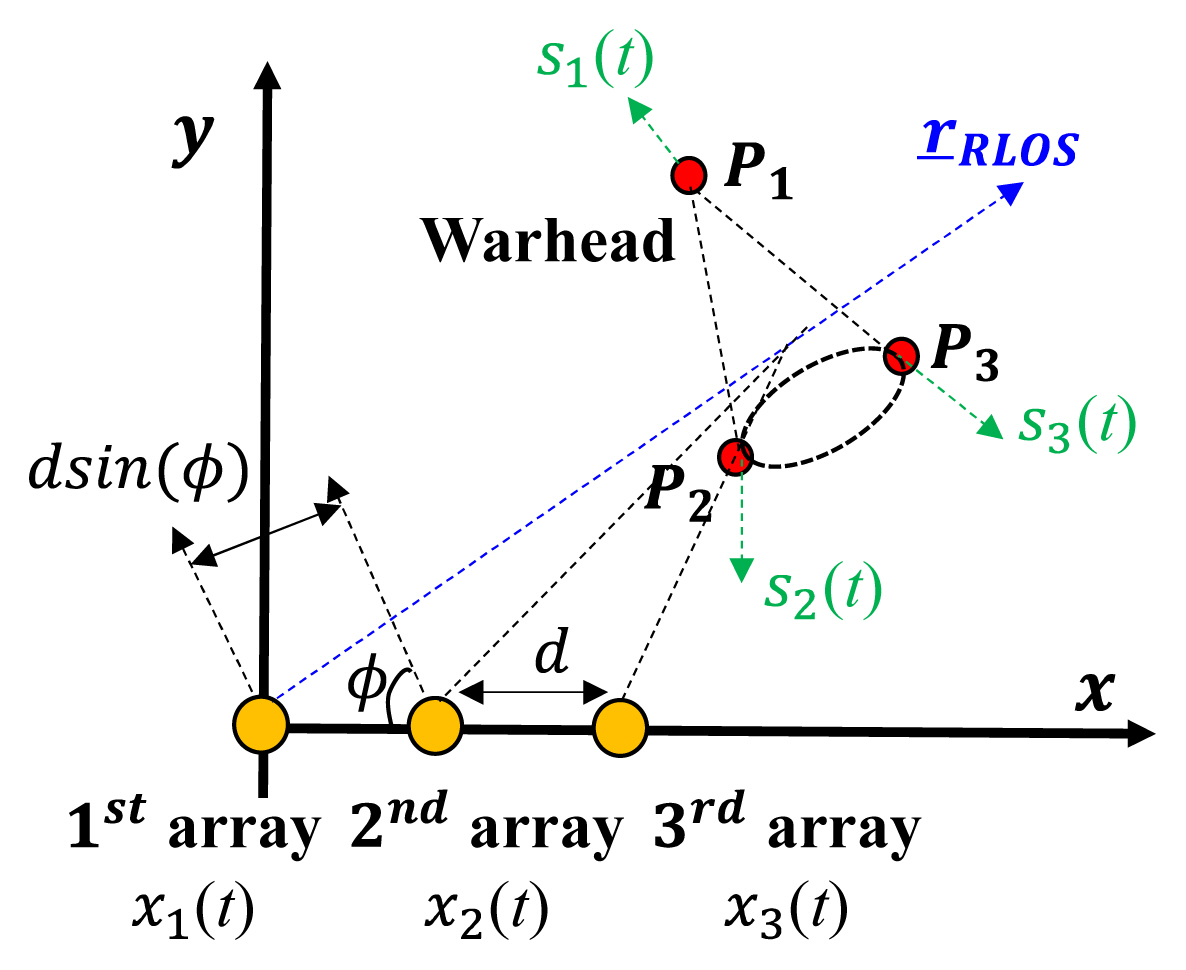
The micromotion of the ballistic warhead is composed of spinning, coning, and nutation; spinning and coning are the rotation around the z-axis, and nutation is the sinusoidal wobbling on the plane formed by the spinning and coning axes (Fig. 1). A simple conical warhead does not have spinning scatterers [14], and thus the micromotion consists only of coning and nutation, unlike in [15]. Assuming that the translational motion of the conical warhead is successfully compensated and that the flight direction is fixed along the z-axis, the rotation by coning at time t around the z-axis can be represented by the Rodriguez rotational formula as follows:
where fc is the coning frequency, I is the identity matrix, and E is the cross-product matrix composed of the x-y-z elements of the unit coning axis [3]. Nutation is expressed by the product of three matrices:
where the superscript T indicates a transpose, AT is the transformation matrix into the coordinate formed by the spinning and coning axes, BT is the rotation matrix by θn(t) = θn0sin(2πfnt) where fn is the nutation frequency, and AT is the transformation matrix back to the original coordinate (refer to [3]).
If scatterer P1 is initially at r10 = [x10, y10, z10]T, its location at t is
the distance to the scatterer along the radar line-of-sight (RLOS) rRLOS is (rRLOS)Tr1(t), and the mathematical model that represents the 1D MD frequency trajectory of the scatterer P1 at t can be defined using (1) and (2) as
where λ is the wavelength. Note that the mathematical model FD(t) composed of six parameters, namely x10, y10, z10, fc, θn0, and fn, can be utilized as the basis function for parameter estimation, leading to a six-dimensional (6D) optimization task, unlike the 10-dimensional (10D) optimization task in [15].
2. Signal Decomposition using the ICA
Individual signals corresponding to multiple scatterers occur simultaneously in the echo signal received from the conical warhead, resulting in a significantly degraded accuracy of the parameter estimation due to mutual interference between individual signals [3, 4]. This problem is easily solved using the ICA, which decomposes the echo signals received from multi-channels into the individual signals corresponding to multiple scatterers.
Assuming that the s(t) = [s1(t), s2(t), …, sN(t)]T is an N × 1 vector of the individual signals corresponding to N scatterers, the x(t) = [x1(t), x2(t), …, xM(t)]T, which is an M × 1 vector of the echo signal received from the M channels of the phased array antenna equally spaced by d at an angle π/2 − φ (Fig. 2), can be written as
where the m-th echo signal xm(t) in x(t) is
and the nth individual signal sn(t) in s(t) is
and
where σm,n is the RCS of the nth scatterer observed by the m-th channel.
ICA obtains the individual signal s(t) by finding W = A−1. After centering and whitening using the eigenvalue decomposition to remove any correlations among the elements of x(t) [16, 17], the nth column vector wn of W can be obtained iteratively using both the fixed-point algorithm and the Newton method given as
where j is the iteration number, z(t) is the transformed x(t) by centering and whitening, the superscript H is a Hermitian transpose, wn(j) is the unit vector of wn at the j-th iteration, and
Subsequently, decorrelation is conducted to make all elements independent:
and this procedure is repeated until W converges.
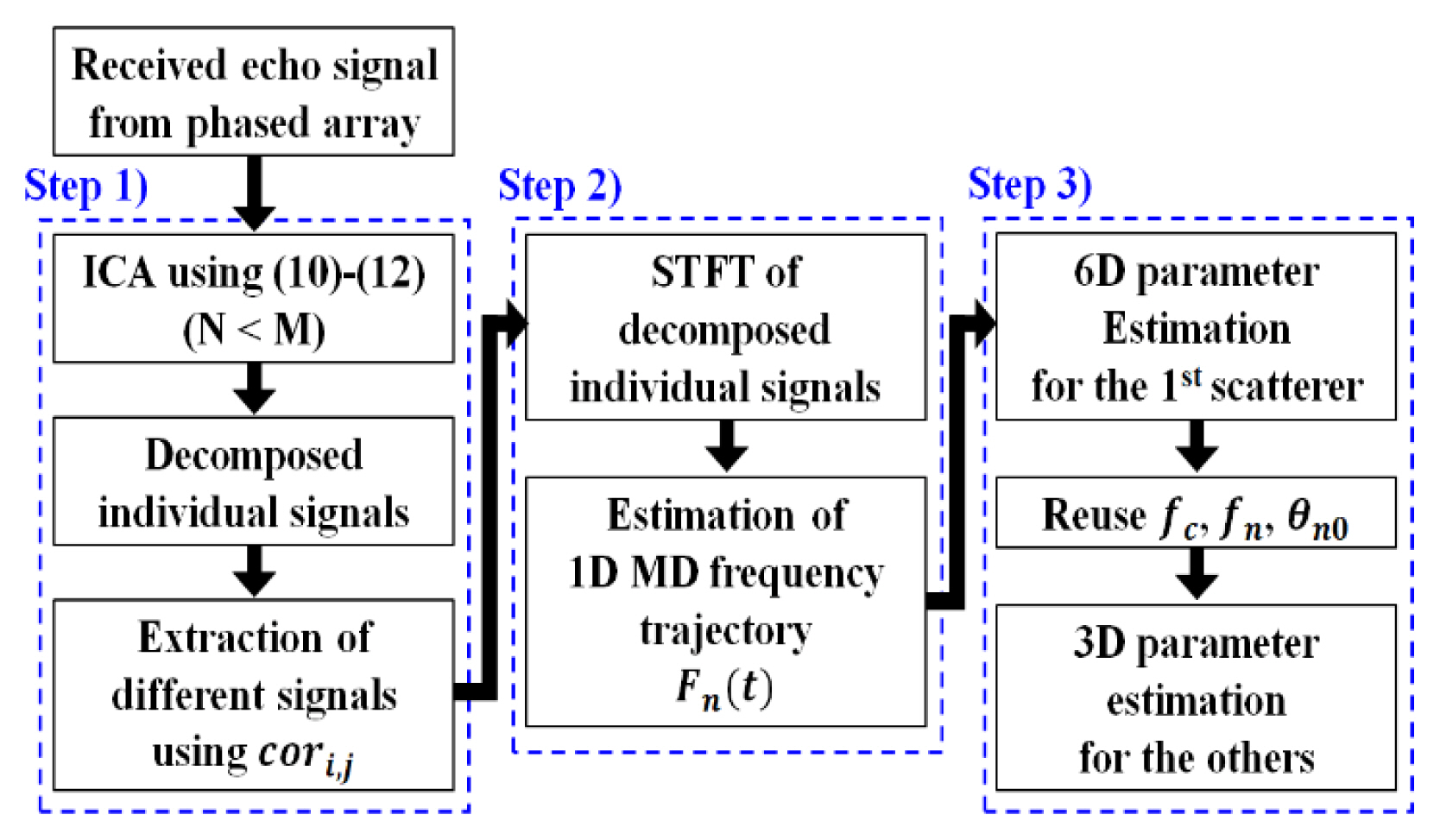
3. Proposed Method
The proposed method is simple and composed of three parts: (i) decomposition of individual signals using ICA, (ii) extraction of 1D MD extraction trajectory from the decomposed individual signal for the n-th scatterer at time t, i.e., Fn(t), and (iii) estimation of parameters using the APSO (Fig. 3). The proposed method is an improved version of the method in [15]. The improvements are (i) a modified signal model for a conical warhead that considers the location and micromotion, thus increasing the accuracy due to the reduced optimization dimension (i.e., 10D → 6D); (ii) insensitivity to noise as a benefit of parameter estimation using the 1D MD frequency trajectory extracted from the 2D JTF image, not the phase information as in [15]; and (iii) verification of the proposed method using the CAD model of the real conical warhead.
The first step applies the ICA using (10)–(12) to x(t), which is composed of the echo signals received from M channels, to yield s(t), which is composed of individual signals corresponding to N scatterers. If N = M, N independent signals are obtained, and if M > N, then M – N signals are repeated in s(t). The existence of the repeated signals is simply found by checking the correlation of two normalized signals in s(t), i.e.,
where T0 is the total observation time. If cori,j ≈ 1, sj(t) is similar to si(t), sj(t) is discarded, and N dissimilar signals are found by repeating the same procedure for all remaining elements in s(t).
The second step extracts the 1D MD frequency trajectory Fn(t) from the decomposed individual signals to estimate the parameters using the mathematical model FD(t) in (4). For this purpose, the 2D JTF image of sn(t) is obtained using the short-time Fourier transform (STFT) in [3–5] as follows:
where T0 is the same as in (13), and w(•) is a proper short-time window function. Then, Fn(t) is found by selecting a Doppler frequency of a maximum peak along the time direction in the 2D JTF image χn(f, t) as follows:
where fs is the sampling frequency. In this step, individual signals s(t) corresponding to each scatterer are decomposed using the ICA, and the 1D MD frequency trajectories Fn(t) are obtained using the STFT for s(t), leading to robustness against noise. Therefore, the parameter estimation using Fn(t) is much more accurate than that using the phase information in [15]. The existing method [15] often fails at estimating the 1D MD frequency trajectories because this method utilizes the phase information of two neighboring elements of the signal in the time domain; these elements are significantly affected by noise. Conversely, in the proposed method, the influence of noise is considerably reduced in the process of coherent signal integration in the STFT (see (14)), yielding an increased accuracy in estimating the 1D MD frequency trajectory Fn(t).
The third step is the 6D optimization task for estimating the parameters, namely xn0, yn0, zn0, fc, θn0, and fn, by maximally matching FD(t) in (4) to Fn(t) in (15) for all n. Owing to the 1D cost function, much time is saved compared with conventional methods [13, 14] that use a 2D JTF image. Note that three parameters, namely fc, fn, and θn0, are common in all individual signals corresponding to each scatterer, and thus the estimation of these values is required only for the first scatterer. Therefore, the dimension of the optimization task is reduced to a 3D space consisting of xn0, yn0, and zn0 for the other scatterers. For the first scatterer, the 6D parameter vector p1 = [x10, y10, z10, fc, fn, θn0]T is obtained as
where [x10, y10, z10]T is the 3D coordinate of the first scatterer in the Cartesian space. Then, the APSO searches for a global particle optimum by changing the parameters, xn0, yn0, zn0, fc, θn0, and fn, in (16). Specifically, the APSO performs a real-time evolutionary state estimation procedure, resulting in improved performance in terms of convergence speed and global optimality over other optimization techniques [18]. The APSO that updates each particle is
where pi is the i-th particle, ppd is the particle’s best, pgb is the swarm’s best, c1 and c2 are the acceleration coefficients, and w is the inertial weight. Using the estimated parameters, such as fc, fn, and θn0, in (16), the coordinate [x20, y20, z20]T of the second scatterer is found using the APSO as follows:
The proposed algorithm is repeated until the coordinates of all scatterers are estimated.
III. Simulation Results
To demonstrate the effectiveness of the proposed method, we considered a conical CAD model (Fig. 4(a)), which is similar to an actual ballistic warhead [4–6]. The echo signals were computed using Virtual Aircraft Framework (VIRAF) software (Table 1). Each array signal (Fig. 2) was constructed by choosing the raw data of the VIRAF corresponding to the aspect angle observed at each RLOS in Table 1. To simulate a received echo signal in a noisy environment, white Gaussian noise was added to achieve the given signal-to-noise ratios (SNRs). The APSO used 100 iterations with 5,000 particles for the first scatterer and 1,000 particles for the others.

(a) CAD model of the conical warhead and (b) 2D JTF image of x1(t) received by the first array at SNR = 25 dB.
The 2D JTF images were formed by applying the STFT to x1(t) at SNR = 25 dB (Fig. 4(b)). Here, the 1D MD frequency trajectories of each scatterer are periodic with a period = 0.1 seconds, and each 1D MD frequency trajectory is slightly distorted due to nutation. Individual signals corresponding to each scatterer are decomposed using the ICA at SNR = 25 dB within 0.02 seconds. MATLAB R2017a that runs on Windows 10 on an Intel i7 processor was utilized for this simulation (Fig. 5). However, the existing methods in [9–14] require exhaustive searching steps for signal decomposition based on the image processing procedure. For example, [14] exhaustively estimates the parameters from the 2D JTF image using the coherent single-range Doppler interferometry, resulting in a computation time of 56.966 seconds. This leads us to conclude that the proposed method is computationally more efficient compared with the signal decomposition based on the image processing procedure in [9–14].
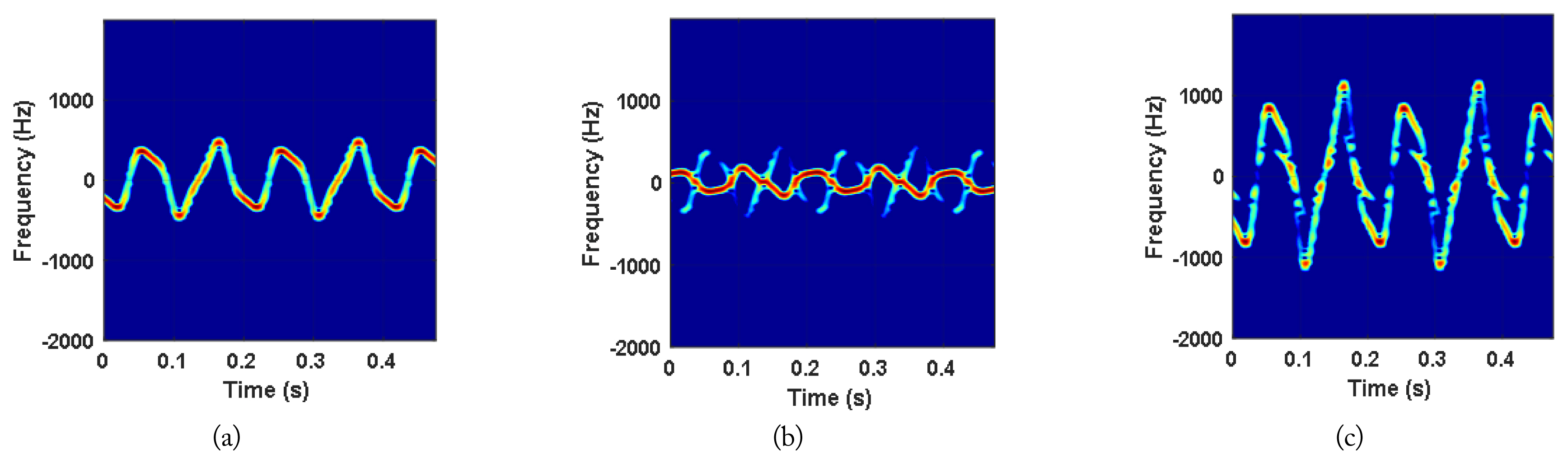
The 2D JTF images of the decomposed individual signals for the CAD model at SNR = 25 dB: (a) s1(t) of the first scatterer, (b) s2(t) of the second scatterer, and (c) s3(t) of the third scatterer.
Fig. 6 shows the 1D MD frequency trajectories extracted using conventional methods in [14] and [15] and the proposed method. Note that the 1D MD frequency trajectories extracted using the conventional method in [15] are contaminated by noise, but these extracted trajectories using other methods are significantly insensitive to noise (Fig. 6). This is due to the fact that the 1D MD frequency trajectories of the proposed method are extracted from the 2D JTF images, not the phase information, as in [15]. However, the conventional method in [14] requires significantly more computation time (e.g., 56.966 seconds) than the proposed method for signal decomposition. In the case of the proposed method, a small amount of the individual signal of the second scatterer overlaps with that of the first scatterer because the individual signal of the first scatterer appears in those of the second and third scatterers. However, these overlaps do not influence Fn(t) because they were removed by appropriate thresholding.
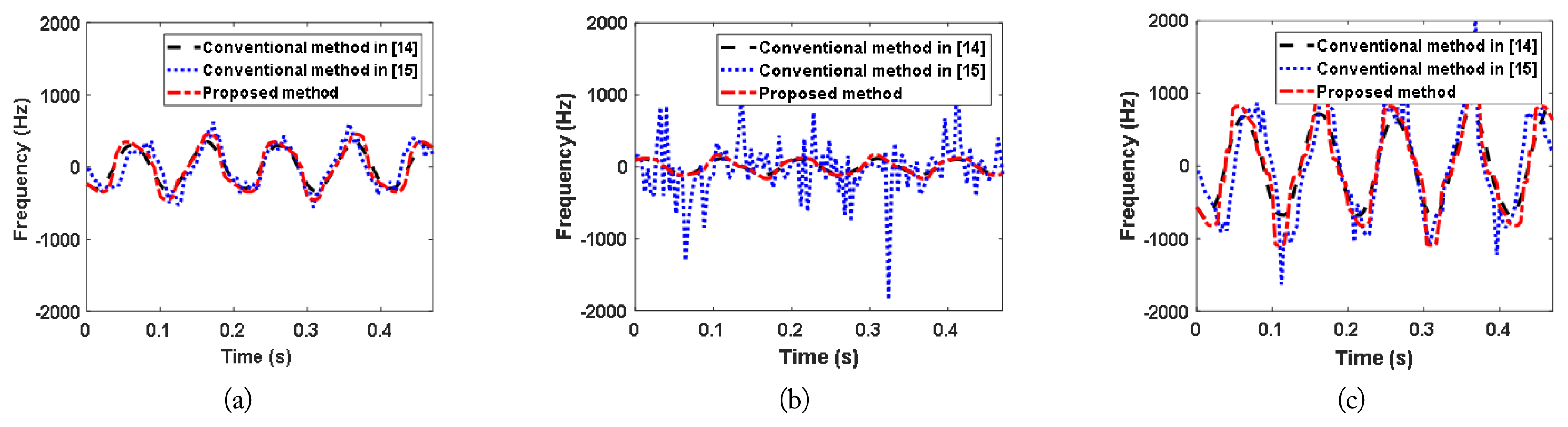
The 1D MD trajectories of the decomposed individual signals for the CAD model at SNR = 25 dB: (a) F1(t) of the first scatterer, (b) F2(t) of the second scatterer, and (c) F3(t) of the third scatterer.
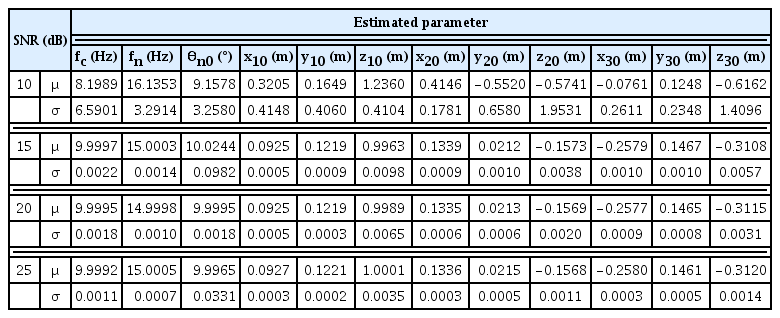
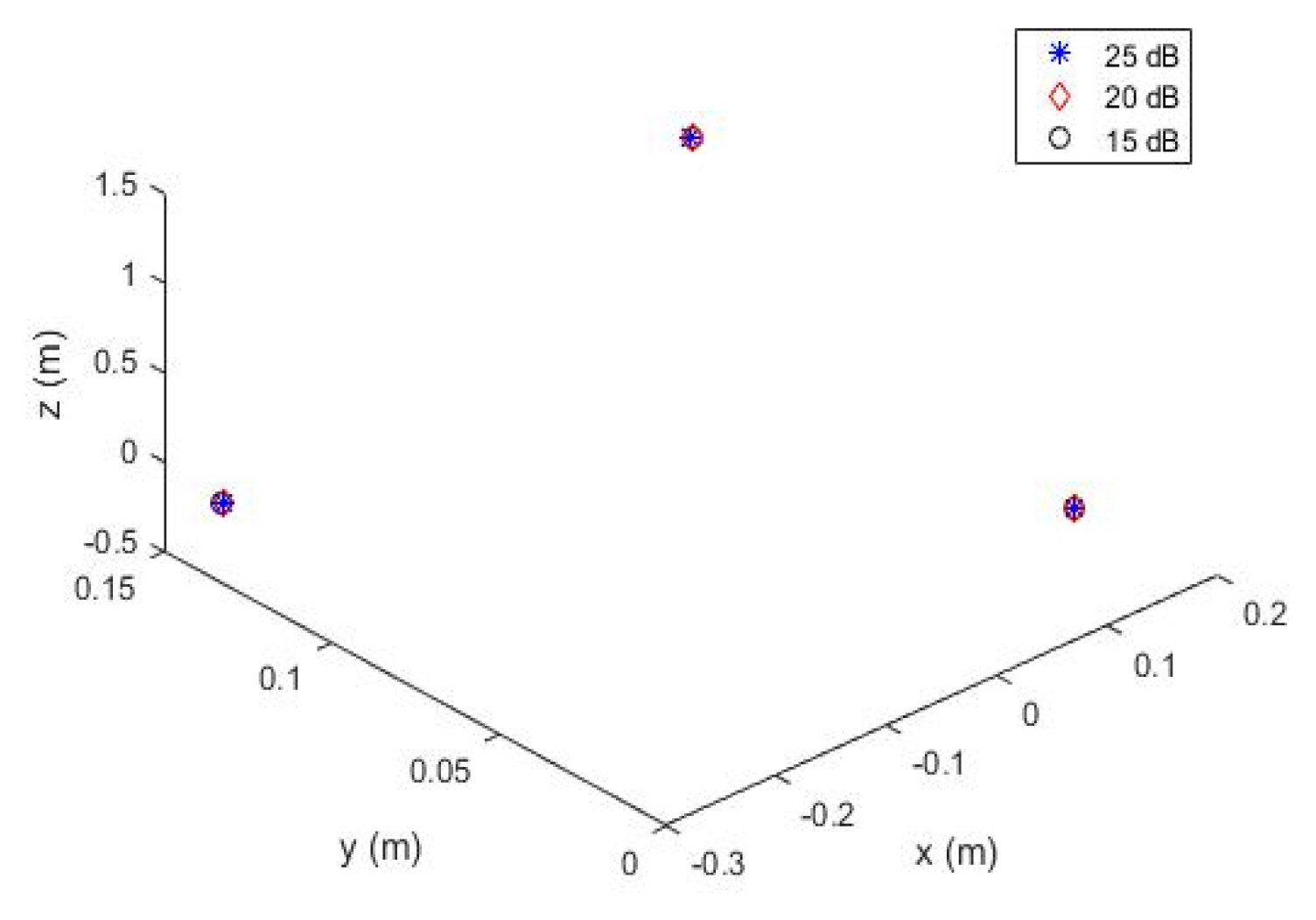
To quantify the accuracy of the parameter estimation, we computed the mean μ and standard deviation σ of the estimated parameters of 100 Monte Carlo simulations, with SNRs = 10, 15, 20, and 25 dB (Table 2). Estimates by the proposed method were not affected by noise when SNR ≥ 15 dB, and the estimated coordinates of the scatterers clearly represented the shape and size of the warhead (Fig. 7). However, the estimation accuracy decreased rapidly at SNR = 10 dB because the noise was louder than the individual signals corresponding to the second and third scatterers, causing the ICA to fail sometimes. Likewise, the simulation results of the conventional method using the high-quality 2D range-time map in [12] show that the mean error related to the estimated parameters of fc, θn0, and fn was 0.07 at SNR = 25 dB due to the weak scatterer signals contaminated by noise [12]. However, the proposed framework can provide a more accurate estimation than the other approaches in [9–12]. We conclude that the proposed scheme provides more accurate parameters of a conical warhead in a noisy environment.
IV. Conclusion
This paper introduces a new framework for an effective estimation of the parameters of a conical warhead with micromotion. The method uses three steps: (i) signal decomposition of individual signals corresponding to each scatterer using the ICA, (ii) extraction of the 1D MD frequency trajectory from the decomposed individual signals, and (iii) estimation of the parameters using the APSO. The simulations using a conical CAD model and VIRAF software demonstrate that the proposed method can decompose the individual signals efficiently and estimate the parameters precisely in a noisy environment.
Acknowledgments
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education, Science, and Technology (No. 2018R1D1A1B07044981).
References
Biography

Inoh Choi received his B.S. and M.S. degrees in electronic engineering from Pukyong National University, Busan, Korea, in 2012 and 2014, respectively and his Ph.D. degree in electronic engineering from Pohang University of Science and Technology, Pohang, Korea, in 2015 and 2019, respectively. He is currently a senior researcher at the Agency for Defense Development, Changwon, Korea. His current research interests include micro-Doppler analysis, ballistic target discrimination, vital sign detection, automotive target recognition, and calibration of polarimetric synthetic aperture radar (SAR).

Jooho Jung received his B.S. degree in the Korea Air Force Academy, Cheongju, Korea, in 1991 and his M.S. and Ph.D. degrees in electronic engineering from Pohang University of Science and Technology (POSTECH), Pohang, Korea, in 1998 and 2007, respectively. From 2008 to 2012, he was a lieutenant colonel in charge of planning national defense research and development in the Defense Acquisition Program Administration, Seoul, Korea. In 2012, he joined the faculty of the Department of Electrical Engineering, POSTECH, where he is currently a research associate professor. He served as the Director of Unmanned Technology Research Center, Korea Advanced Institute of Science and Technology. His research interests are radar target recognition, radar signal processing, and electromagnetic analysis in wind farms by various military radars.

Kyungtae Kim received his B.S. (1994), M.S. (1996), and Ph.D. (1999) degrees in electrical engineering from Pohang University of Science and Technology (POSTECH), Pohang, Korea. From 2002 to 2010, he was a faculty member at the Department of Electronic Engineering, Yeungnam University. Since 2011, he has been with the Department of Electrical Engineering, POSTECH, Pohang, Korea, and he is currently a professor. In 2012–2017, he served as the director of the Sensor Target Recognition Laboratory, which was sponsored by the Defense Acquisition Program Administration and the Agency for Defense Development. Currently, he is the director of both the Unmanned Surveillance and Reconnaissance Technology Research Center and the Radar & ElectroMagnetics Signal Processing (REMS) Laboratory at POSTECH. He is the author of about 200 journal papers and conference proceedings and has been the recipient of several outstanding research awards and best paper awards from the Korea Institute of Electromagnetic Engineering and Science (KIEES) and international conferences. He is a member of the IEEE and of the KIEES. He is currently conducting several research projects funded by the Korean government and several industries. His research interests are mainly in the field of radar signal processing and system modeling: SAR/ISAR imaging, target recognition, direction of arrival estimation, micro-Doppler analysis, automotive radars, digital beamforming, electronic warfare, and electromagnetic scattering.

Sanghong Park received his B.S., M.S., and Ph.D. degrees in electronic engineering from Pohang University of Science and Technology (POSTECH), Pohang, Korea, in 2004, 2007, and 2010, respectively. In 2010, he was a Brain Korea 21 Postdoctoral Fellow at the Electromagnetic Technology Laboratory, POSTECH. In 2010, he joined the faculty of the Department of Electronics Engineering, Pukyong National University, Busan, Korea, where he is currently a professor. His research interests are radar target imaging and recognition, radar signal processing, target motion compensation, and radar cross-section prediction.