Wireless power transfer (WPT) using resonance through magnetic couplings has been actively studied since it was proposed by Soljacic in 2007 [1]. Efficiency analysis of a one-transmitter (Tx) and one-receiver (Rx) system facing each other has been sufficiently performed, and related products can be found in the market. However, the degree of freedom of the receiver positions and postures is still limited. Some studies have been conducted to solve the misalignment problems occurring between Tx and Rx. The misalignment can be divided into two types: axial and angular. A theoretical research on multiple-input single-output (MISO) systems was conducted in [2]. In [3], an energy-efficient and adaptive design method for wireless power transfer in electric vehicles was proposed to alleviate the axial misalignment problem using multiple transmitters. To maximize the power transfer efficiency, the Tx phases and Rx loads were simultaneously optimized based on the same Tx magnitudes. In [4], the solution for the Tx voltages was presented assuming a fixed Rx load. In [5], a plurality of repeaters was attached to the Tx and Rx to solve the misalignment problem. In [6], the three Tx sources with phase differences were used to stably transfer power to an Rx. Through the phase control of orthogonally arranged Tx’s, the direction of the magnetic field was controlled to solve the angular problem [7, 8]. The solutions for the excitation voltage magnitudes and phases for a two-Tx MISO system were numerically found to maximize the efficiency [9].

In this paper, we propose a more general MISO WPT system, the excitation magnitudes and phases and the Rx load of which are simultaneously optimized to achieve maximum efficiencies despite these misalignments. Besides, we obtain the closed-form solution of the excitation voltages for the case of negligible mutual couplings between the Tx’s. In Section II, we briefly summarize the formulas for single-input single-output (SISO) systems and describe the typical two situations in which the power transfer efficiencies become zero. In Section III, based on the derived analytic solution of a two-Tx example, we deduce the solutions of multiple Tx excitation magnitudes and phases for maximum efficiency in a general MISO system. They are validated with the results based on a generic algorithm (GA) and electromagnetic (EM) simulations. The paper is concluded in Section IV.

A SISO system is briefly reviewed to develop formulations for MISO systems. Fig. 1 shows the SISO systems in which axial and angular misalignments occur. In Fig. 1, k is the coupling coefficient [10, 11]. A positive k means the same magnetic flux direction crossing the Tx and Rx loops. A negative k means that the magnetic flux originating from the Tx loop flows into the Rx loop in an opposite direction. A circle is located above the Tx loop where k is zero or very small. Based on the equivalent circuit analysis in [11], efficiency (η) can be expressed as

In (1), P_in is the total input power, P_L is the power supplied to the load with R_L, and b is the normalized load resistance defined by b = R_L/R_{L, opt}, where RL,opt=R01+F2 and F is the figure of merit given by F=kQ1Q2. It is obvious that when b = 1, the efficiency touches an upper bound (maximum). When b > 1 or b < 1, the system becomes under-coupled or over-coupled, respectively, and the efficiencies fall lower than the maximum.

Fig. 2 shows a general MISO system with one Rx loop. The Rx loop is randomly oriented with a tilted angle θ as shown. For the MISO WPT system in Fig. 2, a circuit equation can be written as

where the principal diagonal elements of the Z matrix at the resonant design frequency are

and

In (3) and (4), R_i’s are the loss resistances of the loops, and R_L is the load resistance of the receiver. The remaining elements of [Z], mutual impedances, are given by

where k_ij is the coupling coefficient, L_i is the self-inductance of the loops (or coils), and M_ij is the mutual inductance. The column matrix [I] can be obtained by [Z]⁻¹[V]. The total input power and the received power at the load resistance are

and

respectively. Efficiency is expressed as the ratio of (6) and (7):

To maximize the efficiency (8), we have to optimize the Tx voltage (V₁, V₂, …, V_N) magnitudes and phases and R_L. Finding their analytical solutions considering all the system details given in (2) is usually difficult. Thus, some GA techniques, which are not easily available in industries, must be used to maximize the system efficiency in practice. However, in the case of small mutual impedances or inductances between Tx’s, some convenient solutions for a maximum efficiency can be found.

We start with a simple two-Tx system (N = 2) under the assumption of a negligible coupling between them. For this system, the current flowing on the Rx loop can be analytically obtained as

where Fi=ki0QiQ0, γ = 1 + F₁² + F₂² + β, and β = R_L / R₀. The current flowing on each Tx loop at the resonant freuency can be expressed as

and

where Mi(=ki0LiL0) is the mutual inductance. The input power of each Tx is obtained as

and

where φ is the difference in the excitation phase (φ₁ – φ₂). The total input power and received power are given by

and

respectively. Now, efficiency is expressed as

Defining m = |V₂/V₁|, efficiency (16) is clearly a function of three variables (m, φ, and β) given by

The maximum of (17) occurs in which

and

are simultaneously satisfied. After some algebraic arrangements, the solutions are obtained as

and

Consequently, (22) and (23) can be combined into one equation given by

As indicated, m is a real number. Maximum efficiency is mostly not obtained with the use of V₁ = V₂, which is usually applied in practice. When inserting these solutions into (17), the maximum efficiency is expressed as

where

After further algebraic simplification, (24) results in

where F(=F12+F22) is defined as the figure of merit for a MISO system (N = 2). For a MISO system with N transmitters, we define the system figure of merit as F=∑n=1NFn2. Clearly, (27) has the same form as (1) with b = 1. However, note that this is true only when the couplings between the Tx’s are negligible.

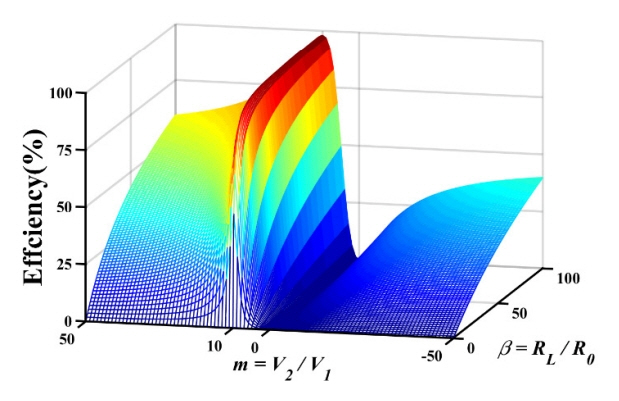
In Fig. 3, we plot the efficiency (17) as a function of m and β for the case of F₁ = 10, F₂ = 100, and R₀ = R₁ = R₂ = 0.01 Ω. Fig. 3 shows that m and β must have specific values to achieve maximum efficiency. When the voltage ratio m = V₂/V₁ = 10 and the normalized load impedance β=1+F12+F22=100.1, as shown in (21) and (24), respectively, efficiency is shown to become maximum (92%). The common practice of using the same Tx voltages (V₂ = V₁) in a MISO may result in a much lower efficiency than the achievable maximum.

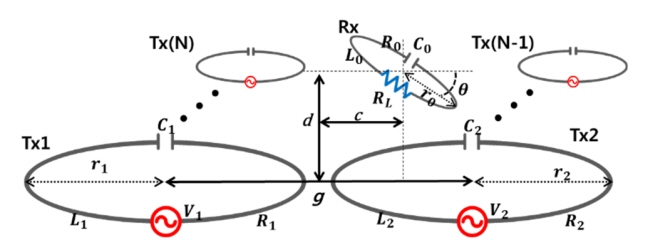
To validate the theory in Section II, circuit and EM simulations are performed for the case of r₁ = r₂ = 6 cm, r₀ = 5 cm, d = 10 cm, c = 0 cm, and g = 20 cm in Fig. 4. The Tx and Rx loops are made of copper rings with a radius of 1 mm. In this case, R₁ = R₂ = 0.0408 Ω, R₀ = 0.034 Ω, L₁ = L₂ = 0.335 μH, and L₀ = 0.266 μH. We choose C₁ = C₂ = 1.65 nF and C₀ = 2.07 nF for resonance at 6.78 MHz. The quality factors Q₁ (or Q₂) and Q₀ are 348.6 and 334.2, respectively. The coupling coefficient (k₂₁) [11] between the two Tx’s is −0.0064. The minus sign implies that the magnetic flux generated from one Tx loop crosses the other in an opposite direction. Thus, the figure of merit F₁₂ = −2.23. The GA in MATLAB (optimization toolbox) is applied to find the optimum magnitude and phase of V₂/V₁ and the Rx load resistance (R_L) through which the efficiency reaches a maximum. EM simulation was performed by ANSYS HFSS using copper loops and lumped C components for resonance. From the EM simulation, we obtain the scattering matrix and coupling coefficients between all copper loops.

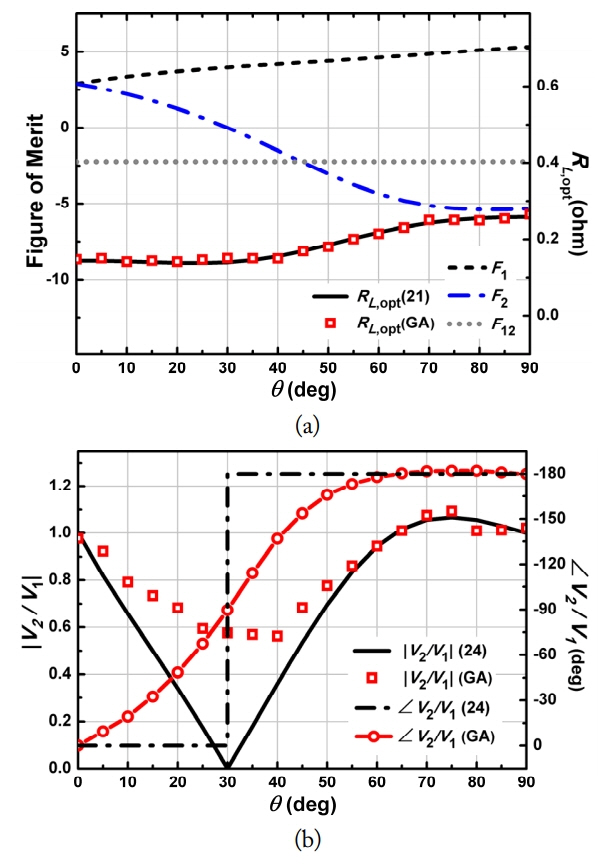
Fig. 5(a) presents the figures of merit (F₁, F₂) and optimum load resistances using the GA and Eq. (21) as a function of the misalignment angle θ at 0°–90°. While F1(=k10Q1Q0) gradually increases from 2.9 to 5.3, F2(=k20Q2Q0) decreases from 2.9 to −5.3 crossing zero at θ = 30°. The negative F₂ comes from the downward magnetic flux on Rx0 when θ > 30°. The magnitude of F₁₂ is shown to be smaller than that of F₁. F₂ changing sign from positive to negative at θ = 30° (F₂ = 0) can be understood by observing the direction of the magnetic flux. The optimum load resistance (R_{L, opt}) (21) is almost the same as the result obtained from the GA even though F₁₂ (= −2.23) is not considered in (21).

Fig. 5(b) shows the optimized magnitude and phase of the voltage ratio (m = V₂/V₁) as a function of the misalignment angle θ using the GA and (24). The magnitudes and phases of V₂/V₁ using the GA and (24) are in agreement except at around θ = 30°. The discrepancies around θ = 30° comes from the fact that, while the assumption made for (24) is the smaller mutual coupling (|F₁| > |F₁₂|) and |F₂| > |F₁₂|), |F₂| is much smaller than |F₁₂| at around θ = 30°.

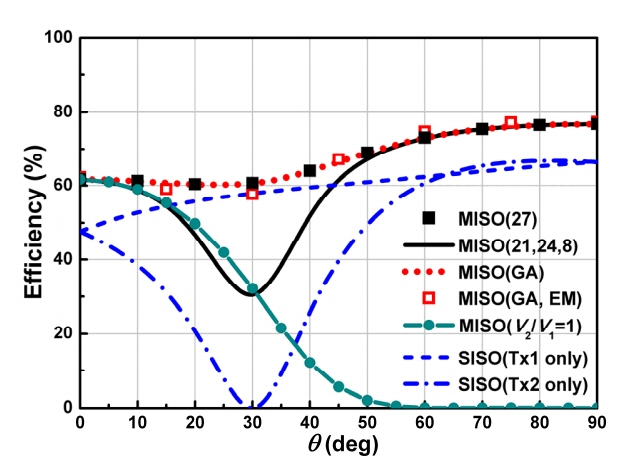
In Fig. 6, the efficiencies based on the GA, Eqs. (21, 24, 8), Eq. (27), and EM-simulation are plotted as a function of the misalignment angle for the same system. The efficiencies for the SISO systems using only Tx1 or Tx2 are also included for comparison. The MISO (21, 24, 8) is calculated by inserting Eqs. (21, 24) into (8). The MISO (27) and MISO (GA) are shown to be in excellent agreement. The EM-simulated efficiency MISO (EM) using |V₂/V₁| (GA) and ∠V₂/V₁ (GA) in Fig. 5(b) also agrees with them. These efficiencies are shown to be higher than those of the SISO systems. The MISO (21, 24, 8) is also shown to be higher than the SISO in which |F₁₂| (= 2.23) is roughly smaller than the system figure of merit F. As |F₁₂| > F, near θ = 30°, we need to optimize the system parameters considering the mutual couplings. However, the evaluation of the maximum MISO efficiency is shown to have been exactly conducted with (27) not depending on the information of mutual coupling. The common practice of using the same Tx voltages (V₂ = V₁) is against the solution (22) and leads to much lower efficiencies than the achievable maximum as shown by MISO (V₂/V₁ = 1) in Fig. 6.

The misalignment problems have been shown to be always solved by MISO through the numerical optimization of Tx excitations (magnitudes and phases). They have been analytically obtained and provided in this study when the mutual inductances are relatively small. Further research is needed to fabricate the proposed MISO system and validate the theory with experimental results.