Photoacoustic Tomography System for Roughly Painted Micro Objects
Article information
Abstract
Subsurface imaging is challenging; it is difficult to detect objects visually. In this research, a novel non-contact photoacoustic (PA) imaging system was developed to detect subsurface objects. The Rosencwaig-Gersho (RG) model was successfully employed to capture micro-object images covered by rough paint. The experiments were conducted using a copper ring with a 1-mm diameter fully coated by rough paint with an average thickness of 2.3 μm. The resulting PA images exhibited up to 72% consistency despite the rough paint; the shapes of the objects were clearly recognized before and after coating. To conduct the experiment, simulations and image acquisitions were arranged. Then, the system capability to produce tomographic images was improved by adjusting the thermal diffusion lengths, and subsurface object images were successfully acquired at depths of 2.0, 2.6, 9.8, and 52 μm. The detailed composition of image slices displayed the structure profile of subsurface objects appropriately.
I. Introduction
Optical imaging plays a significant role in observing defects in objects [1–5]. Its main advantage lies in its broad observation spectrum characteristics and high resolution. However, optimal imaging faces difficulties in observing an object at subsurface levels due to scattering photons and stops at a tissue depth of about 10 μm. This means that the bulk of photons propagating through a tissue slice will experience at least one scattering event, resulting in image blur [6].
Acoustic modality has also been commonly used in subsurface imaging because of its better subsurface attenuations, which utilize piezoelectric materials as transducers for both transmitters and receivers. However, the selection of piezo material must be carefully considered to avoid mismatched impedance and yield optimal efficiency.
To yield optimal efficiency, the air-couple transducer has been developed by combining several impedance-matching materials so that the increase of impedance can be adjusted gradually. However, the minimum focal diameter of such technology is still greater than 1 mm [7, 8]. Therefore, the air-couple technique for acoustic imaging still leads to problems when dealing with micro objects.
Photoacoustic (PA) methods have overcome the challenges found in acoustic coupling by using laser light to excite and probe acoustic disturbances without contacting the sample [9, 10]. Moreover, the laser-driven piezoelectric technology with femtosecond laser pulse has successfully generated acoustic waves in order of terahertz [11].
PA has been reported to detect surface defects in metals [12–14]. With an optical resolution photoacoustic microscopy (OR-PAM) system configuration and water coupling, a full-width at half-maximum (FWHM) of up to 2.5 μm has been accomplished. Nevertheless, defects can also occur at the subsurface level, and these defects are challenging to detect due to invisibilities [15, 16]. Therefore, PA imaging has been used satisfactorily at subsurface levels for applications such as detecting hidden underdrawings in paintings [17]. Indeed, the drawing of a pencil coated with paint can be clearly restored through PA imaging.
In this experiment (subsurface imaging of hidden underdrawings in paintings), direct contact with the object via a water-couple transducer was necessary. Some alternative methods have been employed to create non-contact PA imaging; for example, the all-optical PA microscopy method uses a Fabry-Perot transducer customization [18]. In this study, a novel non-contact PA imaging system was proposed to capture subsurface images without transducer customizations. A PA imaging mesoscopic system and tomography for micro objects using a focused laser beam was developed [19], and the application of the Rosencwaig-Gersho (RG) model to acquire subsurface images was successfully demonstrated [20].
By means of thermal diffusion length adjustment, imaging at a certain depth was accomplished, which generated non-contact tomographic images for micro objects. The experiment object was a copper ring coated by rough paint, and the results showed that the original object shape could be restored completely. Comparisons between pre-coated and coated objects were also performed. The PA images gave superior consistency compared to that of the optical images. Additionally, the system capability to capture tomographic images of an object was also demonstrated. By varying the thermal diffusion length, images could be constructed layer by layer, generating the subsurface structure of the object. The complete experiment results are presented in Section III.
II. Experimental Method
1. Materials
The arrangements of the systems are shown in Fig. 1(a). A modulated laser diode was used to generate thermal contraction of the object. To adjust the thermal diffusion length, a computer-controlled signal generator was employed. Fig. 1(b) shows the interaction between the laser and the coarse surface. There were numerous possible paths, including path 1 and 2. Throughout path 1, the interaction between the laser beam and the material occurred only once, which resulted in a normal absorption coefficient (i.e., dielectric function of the Drude model).
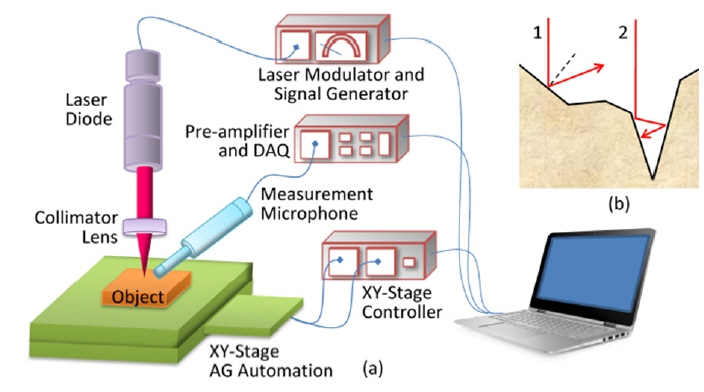
The proposed PA imaging system. (a) The focused laser formed a mesoscopic system in an open cell configuration. (b) For coarse objects, the surface contour resulted in an increasing absorption coefficient (path 2).
Although the electronic interactions were unchanged, the absorption coefficient increased significantly along path 2. This was because the surface geometrical profile captured the light, which led to repeated reflections. A more detailed experiment of this kind was performed in [21], in which the surface roughness level more significantly influenced the absorption coefficient compared to the laser wavelength variation. This conclusion remained consistent even when tested under wider ranges (532–1,064 nm).
Regarding the PA process, this absorption coefficient determined the acoustic initial pressure: p 0 = Γη th βF, where Γ, η th, β, and F are the Gruneisen parameter, energy conversion efficiency, optical absorption coefficient, and laser optical fluence, respectively [22]. Therefore, the PA response on the rough surface was assumed to be insensitive to the laser wavelength variation, and the experiments were conducted using only one wavelength (805 nm, ML520G12; Mitsubishi Electric). A Behringer ECM8000 microphone was utilized to acquire the acoustic waves with a sensitivity of −39.2 dB (11 mV/Pa). The microphone was mounted 10 mm away from the object, forming a 45° angle with the normal line. The collimator lens used was the Mitutoyo Objective Lens BD Plan Apo 7.5×, whose parameters are specified in Table 1.
The tested material was a copper ring with a thickness of 0.05 mm and an outer diameter of 1 mm. The ring lay on the surface of an acrylic printed circuit board. Different object and background materials were chosen to acquire better PA image contrast resulting from different thermal properties. As a comparison, a standard air-couple-based imaging system—namely, the Examet Union 81837 digital microscope (Ogawa Seiki Co. Ltd.)—was used.
2. PA Multilayer Analysis
According to the RG model, the PA amplitude (Q PA ) correlates with the thermal diffusion length of the material. Thus, Q PA specifies the complex envelope of the sinusoidal pressure variation in the form of acoustic magnitude generated by the PA process. For opaque materials (μ a << l, μ a << μ s ), Q PA is proportional to two states, as follows:
where f, α, and k are laser modulation frequency, diffusivity, and thermal conductivity of the material, respectively [23]. Indices a and s in μ represent air and solid. Afterward, index j is used to represent the order of solid layers. Meanwhile, μ j and l j are thermal diffusion length and material thickness, respectively. The first state occurs when the material is under thermally thin conditions (e.g., μ j > l j ), whereas the contrary condition is called thermally thick. The two conditions can be achieved by adjusting laser modulation frequency using the following equation:
Eq. (1) shows that the PA amplitude depends on the comparison of the thermal diffusion length and the thickness of the material. Therefore, any alteration of layers can be discovered by gradually varying the modulation frequency. When the modulation frequency satisfies the condition μ j < l j , the PA amplitude can be determined by the material at layer j. However, when the frequency is varied until it satisfies the condition μ j > l j , the amplitude changes drastically according to the (j + 1)th layer’s characteristics.
III. Results and Discussion
1. Modeling and Simulation
The interaction scheme between the thermal diffusion length and the paint depth is shown in Fig. 2(a). Rough paint was characterized by the thickness of the paint (l paint ) that enclosed the object surface. According to Eq. (1), three possible conditions existed: μ paint < l paint , μ paint = l paint , and μ paint > l paint . The first condition took place when the paint coat was thicker than its thermal diffusion length and the PA amplitude was determined by the first material layer, Q PA (μ paint , k paint ). When the paint coating layer was thinner than its thermal diffusion length, the third condition was satisfied, and the amplitude became Q PA (μ object , k object ). Theoretically, despite the variation of the paint depth, the PA amplitude did not respond directly. Any alteration occurred only when the paint coat thickness exceeded the threshold of the thermal diffusion length. This became the principal difference between optical and PA imaging due to insensitivity to the surface roughness. The second condition occurred when the paint coat thickness was the same as the thermal diffusion length. Then, the Q PA experienced a transition from the preceding two conditions.

(a) The resulting amplitude Q PA due to various surface roughness. (b) The cross section of the roughly-coated copper ring model on 500 × 500 pixels. Simulations of PA images with a roughness mean of 2.0 μm (c) and 3.0 μm (d), where μ paint = 2.46 μm.
To run simulations, a number of computations were performed using GNU Octave version 5.1.0 programming. To generate a PA image, Eq. (1) was employed with each associated material parameter. To establish the object, an array was constructed with a dimension of 500 × 500 pixels, on which a copper ring was laid as shown in Fig. 2(b). For simulation purposes, the rough paint was assumed to have a normal distribution with a mean of 2 μm and 3 μm. These values were chosen to approach the thermal diffusion length of the paint, which was 2.46 μm (α paint = 2.1 × 10−7 m2/s at modulation frequency of 11 kHz). Thus, the distributions above and below the mean were expectedly balanced.
The PA image resulting from the simulation using these parameters is depicted in Fig. 2(c) for μ paint > l paint , where l paint was the average thickness of the paint. The copper region gave weaker Q PA in the order of about 0.39 × 10−9 (a.u). At this state, the shape of the copper ring was displayed clearly because its thermal property significantly affected the Q PA . Since the thermal conductivity of copper was far different than that of the background (k copper = 386 W/mK and k acrylic = 0.40 W/mK), the pixel intensity level could be distinctly discriminated and therefore yielded a higher image contrast.
When l paint was increased to 3.0 μm, the results changed, as shown in Fig. 2(d). At this state, the condition of μ paint < l paint was more likely to happen, and the amplitude Q PA was dominated only by the paint’s thermal property. Since the thermal conductivity of the paint (k paint = 1.45 W/mK) was much closer to that of the background (acrylic), the resulting Q PA parameters were similar in the order of 4.5 × 10−9 (a.u). Due to this similarity of pixel intensity levels, the image contrast decreased, and the copper ring image became blurred.
2. Roughly Painted Object Imaging
Fig. 3(a) shows the object image prior to being coated. By adhering to the prior simulation parameters, a modulation frequency of 11 kHz and a rough paint coating with an average depth of 2.3 μm were used. A commercial acrylic epoxy spray paint (Dull Black-4, RJ London) was applied gradually. The subsequent layer was applied immediately after the previous layer to avoid multilayer coating. After accomplishing the coating process, the average paint depth was measured using the Mitutoyo 193-111 micrometer.
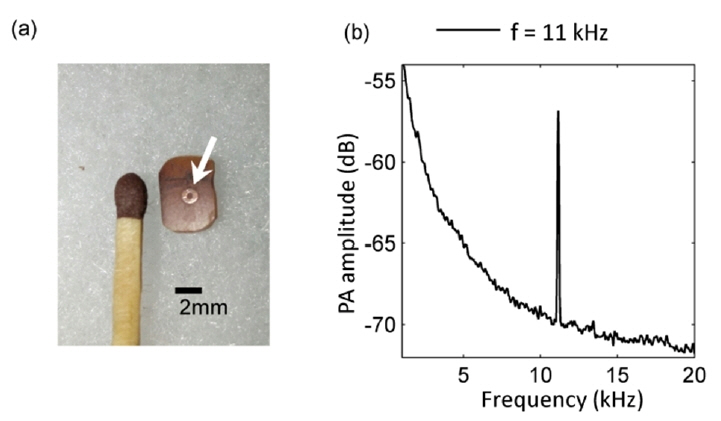
(a) Photograph of the copper ring prior to being coated, as indicated by the arrow. (b) The PA signal response with a modulation frequency of 11 kHz.
At the initial stage, a single object point was measured, and the signal was recorded for 0.5 seconds. Then, Fourier transformation was performed to obtain the signals spectrum (Fig. 3(b)). Since an open cell configuration was used, the position of the microphone could be arranged to obtain the optimum result. The signal Q PA was intensely detected with a peak of 11 kHz in accordance with the modulation frequency. The spectrum exhibited a microphone response up to 20 kHz with a background intensity of −70 dB and a peak of up to −57 dB. Due to this large difference, the PA signal could be detected directly.
Prior to measurements, the object image was captured by means of a microscope. The optical pre-coated object image is shown in Fig. 4(a). Visually, the image possessed an excellent quality with high and evenly distributed contrast so that the object shape could be acquired clearly. However, a different result arose for the coated object, as depicted in Fig. 4(b). The rough paint coat created many disturbances in the form of light reflections and randomly distributed high absorbance; as a consequence, the object was barely displayed.

Object image captured by microscope (a, b, c) and PA (d, e, f). (a) and (d) are real object images. (b) and (e) are images of the coated objects. (c) and (f) are subtractions of the two previous images, followed by normalization. (g) and (h) are LSF curves for optical and PA image, respectively. Index “sub” corresponds to LSF for roughly painted and coated objects.
Next, the experiments for PA imaging were conducted using same object. The first scanning result is shown in Fig. 4(d). The PA image showed a high contrast, as was expected from the prior simulation. The object shape was easy to recognize and, accordingly, could be shown as a whole.
Fig. 4(e) shows the PA image of the roughly coated object. Both PA images did not indicate significant changes visually, regardless of the presence of coating. To test this consistency, image subtractions for both modalities were conducted after normalizing each image. The result for the optical images is shown in Fig. 4(c). The inconsistency of the object intensities before and after the coating process were shown; thus, the image subtraction failed to display the object completely. Unlike the optical image, the PA images gave better consistency, and the corresponding image subtraction displayed the real object shape, as shown in Fig. 4(f).
Furthermore, line spread function (LSF) curves were established for all images, as shown in Fig. 4(g) and (h). As indicated before, the optical image had a large change of LSF curves (Fig. 4(g)). Therefore, it could be inferred that the curve widened due to the rough paint coating. The FWHM measurement implied a change of values from 4 μm to 34 μm, giving a consistency of only 12%. The PA images, however, had a smaller change (i.e., from 55 μm to 76 μm), giving a consistency of up to 72%.
3. Tomography Object under Paint
The tomography process was carried out by adjusting the penetration depth by changing the value of the thermal diffusion length of the first layer (paint), as given by Eq. (2). In this experiment, four different frequencies were employed: 15.8 kHz, 12.5 kHz, 9.7 kHz, and 1.5 kHz. These corresponded to thermal diffusion lengths of 2.0 μm, 2.6 μm, 9.8 μm, and 52 μm. These frequencies were chosen so that the image slices were distributed to distinct layer depths. Then, the laser beam energy for each modulation was measured using a laser power meter (Sanwa LP1); the results are shown in Table 2.
The resulting tomographic images associated to object depths are shown in Fig. 5(a). When the thickness of the paint coating and copper ring were 2.3 μm and 50 μm, respectively, the image slice for the inner part of the paint coat could be obtained with a modulation of 15.8 kHz (Fig. 5(b)). When the frequency was decreased to 12.5 kHz, the image slice arose from the paint–ring junction, as shown in Fig. 5(c). Since it the image slice was closer to the ring surface, several scratches were seen on the image, as indicated by the arrows in Fig. 5(c). Furthermore, when the frequency was decreased to 9.7 kHz, the middle of the copper ring could be observed (Fig. 5(d)).

The tomography process used four different frequencies, which were 15.8, 12.5, 9.7, and 1.5 kHz, corresponding to μ paint of 2.0, 2.6, 9.8, and 52 μm, respectively.
At this depth, the copper’s thermal property dominated the establishment of the PA amplitude, as in Eq. (1). Therefore, the resulting image was different from the two preceding images. Compared to the previous images, the intensity of the ring was darker than its background because the thermal conductivity of copper was higher than that of the paint, and the magnitude Q PA decreased. This transition process also verified that the tomography process occurred at the desired layer. When the frequency was further decreased to 1.5 kHz, the thermal diffusion length of the copper ring surpassed its thickness so that PA imaging produced the base layer image, as shown in Fig. 5(e). At this frequency, the thermally thin condition was satisfied. Therefore, the copper ring became photo-acoustically transparent. In this transparent condition, PA imaging penetrated through the ring and captured the image below it.
IV. Conclusion
A PA imaging system was developed for opaque micro objects coated by rough paint. This imaging method was robust against disturbances and was able to display the objects clearly. Furthermore, it demonstrated effectiveness in providing tomographic images by means of thermal diffusion length according to the RG model. By using this simple method, the three-dimensional condition of the object could be reconstructed in accordance to the desired depth. Despite the aforementioned facts, the PA FWHM value was still much lower than that of the optical image. This was mainly due to the X-Y stage accuracy used during the scanning process; this accuracy enhancement was expected to improve the captured PA image.
Acknowledgments
This work was supported by the Universitas Kristen Satya Wacana through Fundamental Research Grant with S.K. No. 062/Penel./Rek./3/V/2019.
References
Biography
Andreas Setiawan is a lecturer at the Department of Physics, Universitas Kristen Satya Wacana. He received a bachelor’s degree in physics instrumentation from the Universitas Kristen Satya Wacana, Indonesia, in 1999 and a master’s degree in instrumentation and control from the Institute of Technology, Bandung, Indonesia. He received a doctorate at the Department of Physics, Gadjah Mada University, Indonesia, focusing on photoacoustic instruments for practical applications.

Gunawan Dewantoro received his bachelor’s degree from Gadjah Mada University, Yogyakarta, in 2008. He earned his master’s degree from National Taiwan University of Science and Technology in 2011. His interests include control theory, optimizations, and intelligent systems. He has been with Universitas Kristen Satya Wacana since 2012.

Fransiscus Dalu Setiaji received a bachelor’s degree in electrical engineering at the Universitas Kristen Satya Wacana, and his master’s degree is in the same field from Gadjah Mada University. He currently works as a lecturer at the Department of Electrical and Computer Engineering, Universitas Kristen Satya Wacana. His interests include teaching and research in photoacoustic imaging.

Nur Aji Wibowo received his bachelor’s and master’s degrees in physics from Sebelas Maret University, Indonesia, in 2007 and 2011, respectively. He currently works as a lecturer in the Physics Department of the Faculty of Science and Mathematics in Universitas Kristen Satya Wacana, Indonesia. His fields of research interest include optical thin film, spintronic, nano-magnetic particles, and magnetized fuel.


