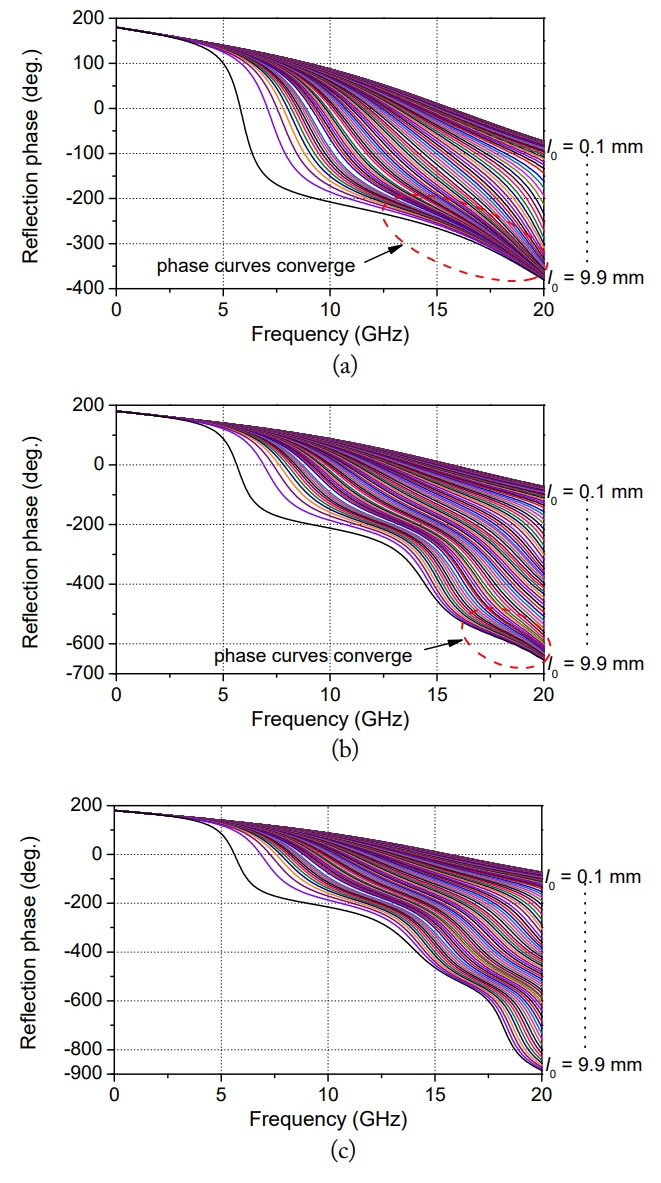
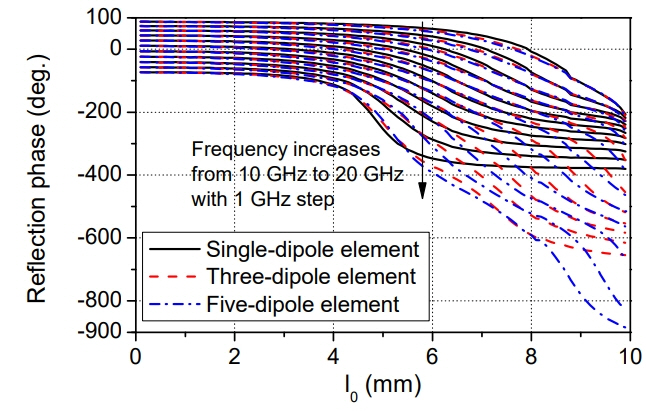
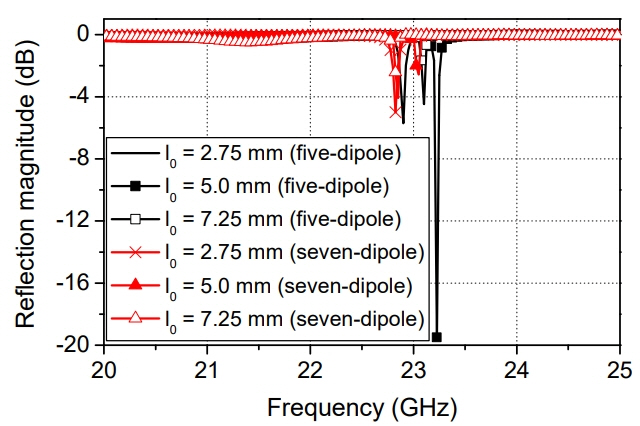
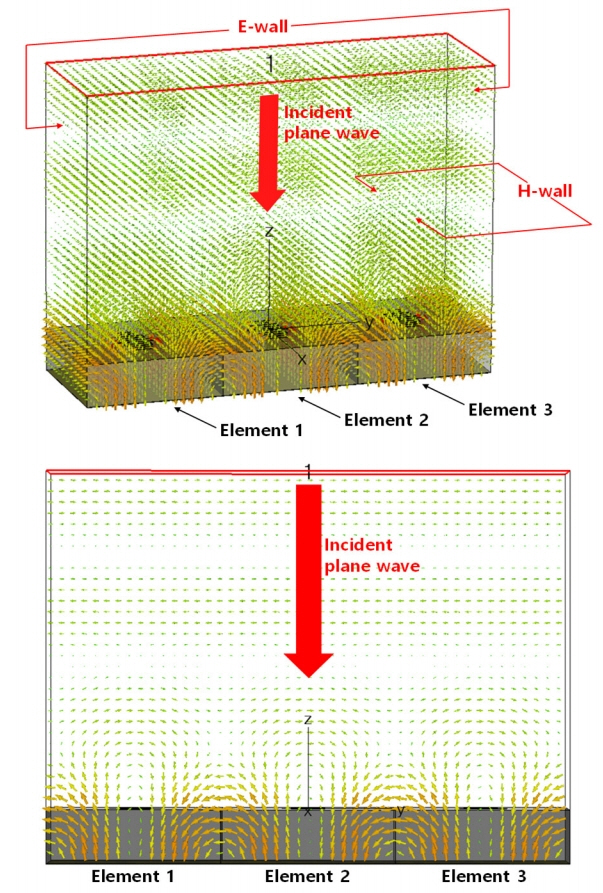
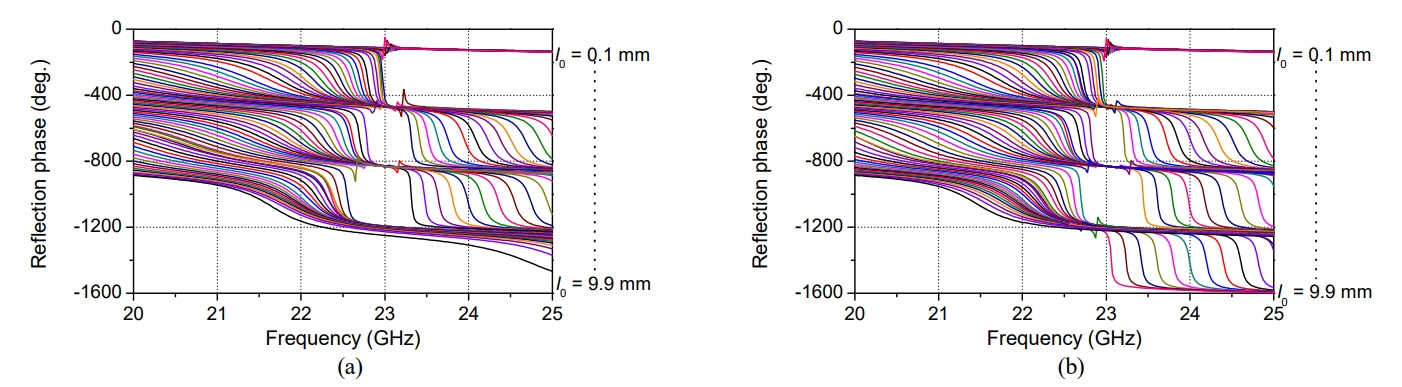
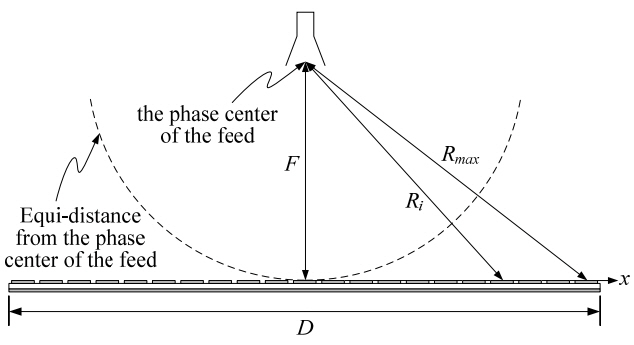
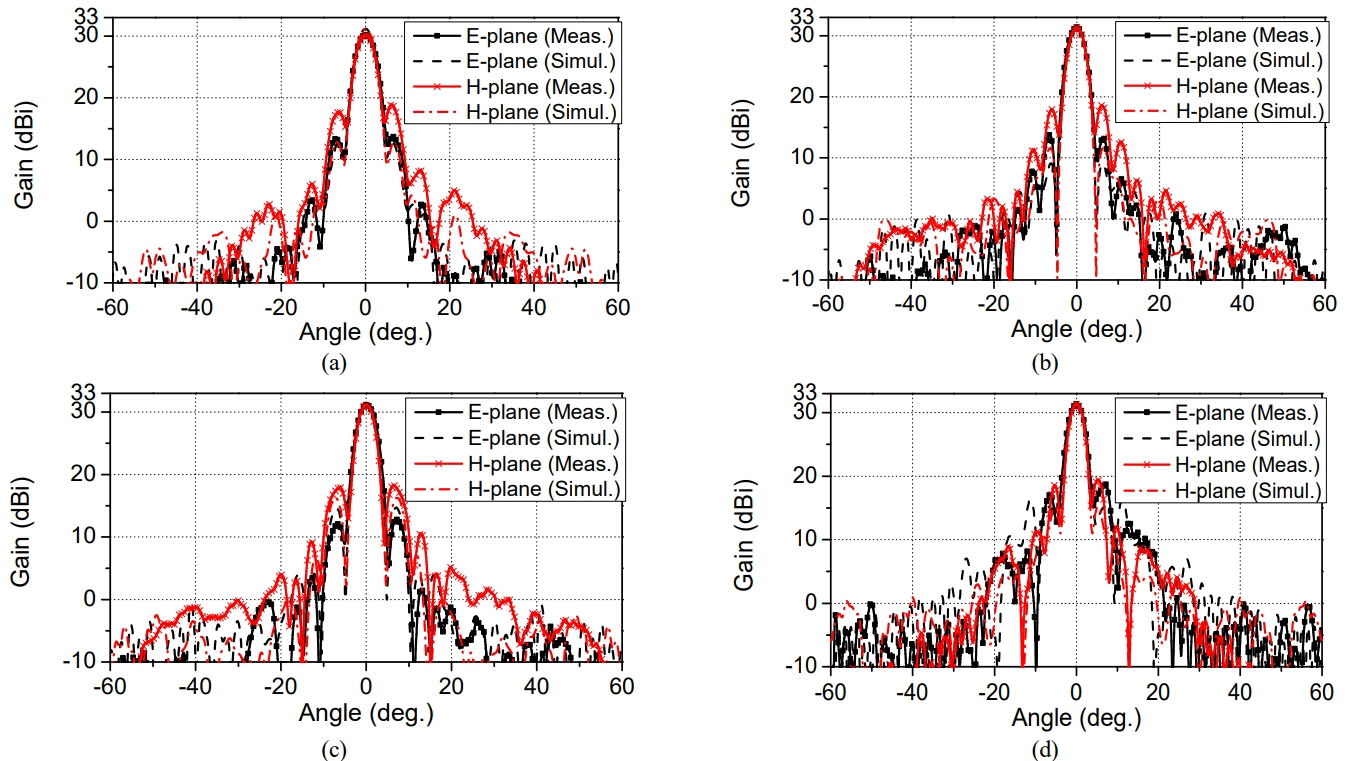
1. J Huang and JA Encinar, Reflectarray Antennas. Hoboken, NJ: Wiley-IEEE Press, 2008.
2. QY Chen, SW Qu, JF Li, Q Chen, and MY Xia, "An X-band reflectarray with novel elements and enhanced bandwidth,"
IEEE Antennas and Wireless Propagation Letters, vol. 12, pp. 317ŌĆō320, 2013.

3. QY Chen, SW Qu, XQ Zhang, and MY Xia, "Low-profile wideband reflectarray by novel elements with linear phase response,"
IEEE Antennas and Wireless Propagation Letters, vol. 11, pp. 1545ŌĆō1547, 2012.

4. R Florencio, RR Boix, E Carrasco, JA Encinar, M Barba, and G Perez-Palomino, "Broadband reflectarrays made of cells with three coplanar parallel dipoles,"
Microwave and Optical Technology Letters, vol. 56, no. 3, pp. 748ŌĆō753, 2014.

5. JH Yoon, YJ Yoon, WS Lee, and JH So, "Broadband microstrip reflectarray with five parallel dipole elements,"
IEEE Antennas and Wireless Propagation Letters, vol. 14, pp. 1109ŌĆō1112, 2015.

6. A Vosoogh, K Keyghobad, A Khaleghi, and S Mansouri, "A high-efficiency Ku-band reflectarray antenna using single-layer multiresonance elements,"
IEEE Antennas and Wireless Propagation Letters, vol. 13, pp. 891ŌĆō894, 2014.

7. JA Encinar, "Design of two-layer printed reflectarrays using patches of variable size,"
IEEE Transactions on Antennas and Propagation, vol. 49, no. 10, pp. 1403ŌĆō1410, 2001.

8. J Encinar and JA Zornoza, "Broadband design of a three-layer printed reflectarray,"
IEEE Transactions on Antennas and Propagation, vol. 51, no. 7, pp. 1662ŌĆō1664, 2003.

9. MR Chaharmir and J Shaker, "Broadband reflectarray with combination of cross and rectangle loop elements,"
Electronics Letters, vol. 44, no. 11, pp. 658ŌĆō659, 2008.

10. MR Chaharmir, J Shaker, and H Legay, "Broadband design of a single layer large reflectarray using multi cross loop elements,"
IEEE Transactions on Antennas and Propagation, vol. 57, no. 10, pp. 3363ŌĆō3366, 2009.

11. JH Yoon, JS Kim, YJ Yoon, WS Lee, and JH So, "Single-layer reflectarray with combination of element types,"
Electronics Letters, vol. 50, no. 8, pp. 574ŌĆō576, 2014.

12. JH Yoon, YJ Yoon, WS Lee, and JH So, "Wband microstrip reflectarray with double-cross element for bandwidth improvement," In:
Proceedings of Global Symposium on Millimeter-Waves (GSMM); Montreal, Canada. 2015, pp 1ŌĆō3.

13. D Pozar and D Schaubert, "Scan blindness in infinite phased arrays of print diploes,"
IEEE Transactions on Antennas and Propagation, vol. 32, no. 6, pp. 602ŌĆō610, 1984.

14. D Pozar and D Schaubert, "Analysis of an infinite array of rectangular microstrip patches with idealized probes feeds,"
IEEE Transactions on Antennas and Propagation, vol. 32, no. 10, pp. 1101ŌĆō1107, 1984.

15. H Rajagopalan and Y Rahmat-Samii, "On the reflection characteristics of a reflectarray element with low-loss and high-loss substrates,"
IEEE Antennas and Propagation Magazine, vol. 52, no. 4, pp. 73ŌĆō89, 2010.

16. KK Karnati, Y Yusuf, S Ebadi, and X Gong, "Theoretical analysis on reflection properties of reflectarray unit cells using quality factors,"
IEEE Transactions on Antennas and Propagation, vol. 61, no. 1, pp. 201ŌĆō210, 2013.

17. AK Bhattacharyya, Phased Array Antennas: Floquet Analysis, Synthesis, BFNs and Active Array Systems. New York, NY: John Wiley & Sons, 2006.
18. PD Patel, "Approximate location of scan-blindness angle in printed phased arrays,"
IEEE Antennas and Propagation Magazine, vol. 34, no. 5, pp. 53ŌĆō54, 1992.

19. DM Pozar, "Rigorous closed-form expressions, for the surface wave loss of printed antennas,"
Electronics Letters, vol. 26, no. 13, pp. 954ŌĆō956, 1990.

20. JS Kim, JH Yoon, YJ Yoon, WS Lee, and CG Kim, "Design of modified dual mode horn antenna to improve E/H-plane radiation pattern symmetry," In: Proceedings of 2012 International Symposium on Antennas and Propagation (ISAP); Nagoya, Japan. 2012, pp 547ŌĆō550.