1. TH Kim, JW Yi, and YJ Byun, "Real-time selection of pulse repetition frequency (PRF) set for a triple 2-of-3 PRF scheme,"
Journal of Electromagnetic Engineering and Science, vol. 13, no. 3, pp. 186–188, 2013.

2. P Georges, "Phased array antenna: is it worth the cost on a fighter aircraft? In:
Proceedings of IEEE Conference on Aerospace and Electronics; Dayton, OH. 1990, pp 312–316.

3. Y Bar-Shalom, Multitarget-Multisensor Tracking: Applications and Advances. Norwood, MA: Artech House, 1992.
4. PL Bogler, Radar Principles with Applications to Tracking Systems. New York, NY: John Wiley & Sons, 1990.
5. A Wald, Sequential Analysis. New York, NY: Dover Publications, 1973.
6. HM Finn, "A new approach to sequential detection in phased array radars," In: Proceedings of IEEE National Winter Convention Military Electronics; Los Angeles, CA. 1963.
7. LF Brennan and FS Hill, "A two-step sequential procedure for improving the cumulative probability of detection in radars,"
IEEE Transactions on Military Electronics, vol. 9, no. 3, pp. 278–287, 1965.

8. EH Kim and JE Roh, "Calculation of the detection range for a given cumulative probability in airborne surveillance radars,"
The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 29, no. 1, pp. 24–27, 2018.

9. JD Mallett and LE Brennan, "Cumulative probability of detection for targets approaching a uniformly scanning search radar,"
Proceedings of the IEEE, vol. 51, no. 4, pp. 596–601, 1963.

10. MB Ringel, DH Mooney, and WH Long, "F-16 pulse Doppler radar (AN/APG-66) performance,"
IEEE Transactions on Aerospace and Electronic Systems, vol. 19, no. 1, pp. 147–158, 1983.

11. WH Long and KA Harriger, "Medium PRF for the AN/APG-66 radar,"
Proceedings of the IEEE, vol. 73, no. 2, pp. 301–311, 1985.

12. E Grossi, M Lops, and L Venturino, "A new look at the radar detection problem,"
IEEE Transactions on Signal Processing, vol. 64, no. 22, pp. 5835–5847, 2016.

13. E Grossi, M Lops, and L Venturino, "Analysis of two-step sequential detection in pulse radars," In:
Proceedings of 2017 IEEE Radar Conference; Seattle, WA. 2017, pp 0535–0539.

14. N Levanon, Radar Principles. New York, NY: Wiley, 1988.
15. P Swerling, "Probability of detection for fluctuating targets,"
IRE Transactions on Information Theory, vol. 6, no. 2, pp. 269–308, 1960.

16. PJ Fielding and AM Kinghorn, "Waveform optimisation for efficient resource allocation in airborne AESA radar systems," In:
Proceedings of IEE Multifunction Radar and Sonar Sensor Management Techniques; London, UK. 2001.

17. E Aronoff and NM Greenblatt, "Medium PRF radar design and performance," In: the 20th Tri-Service Radar Symposium; 1974.




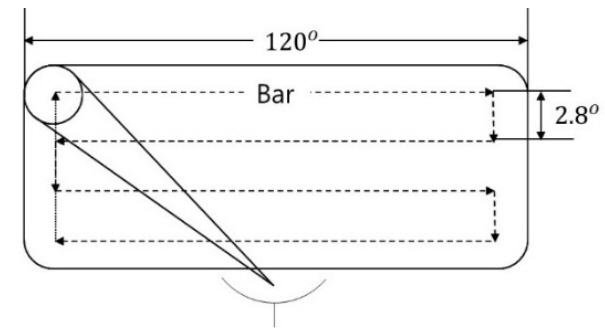
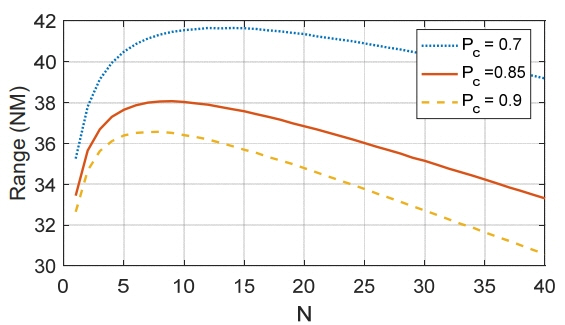


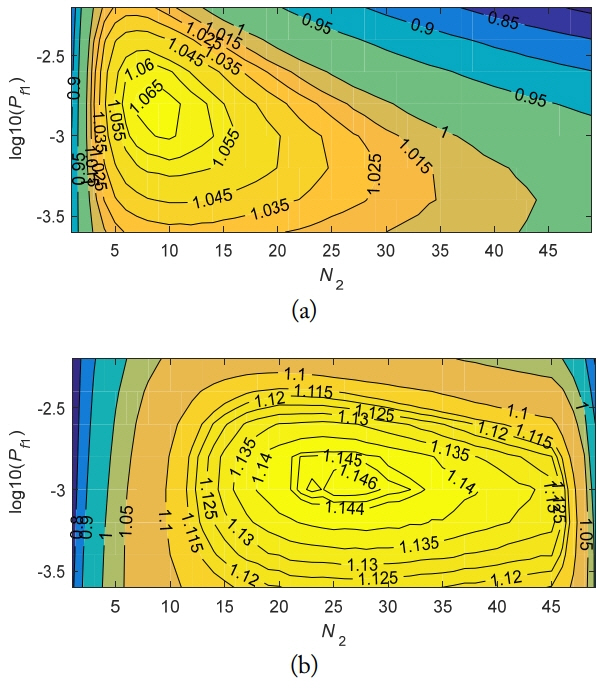
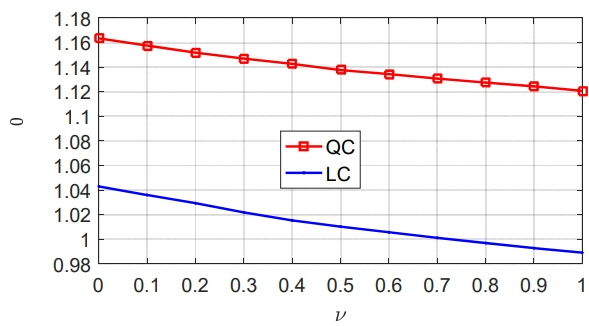
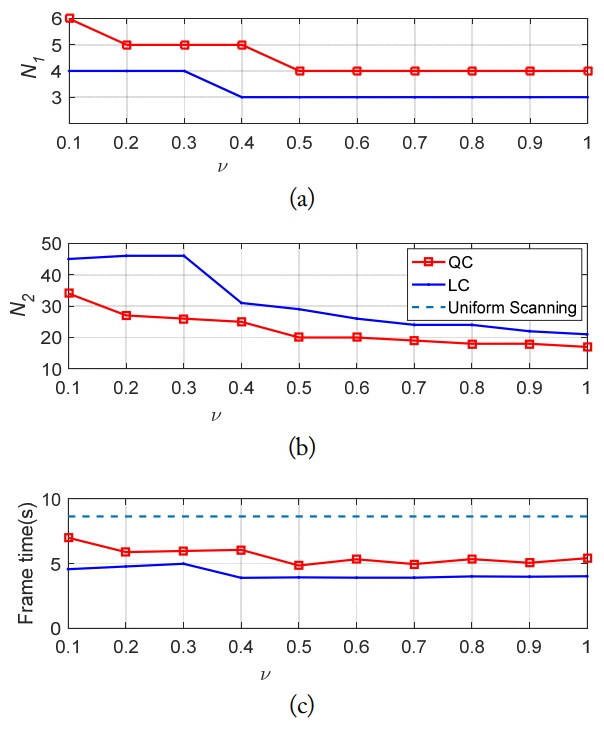
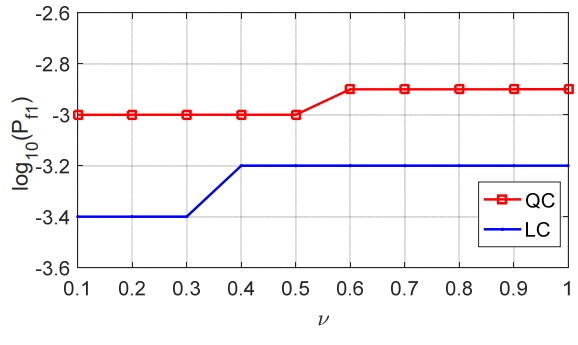
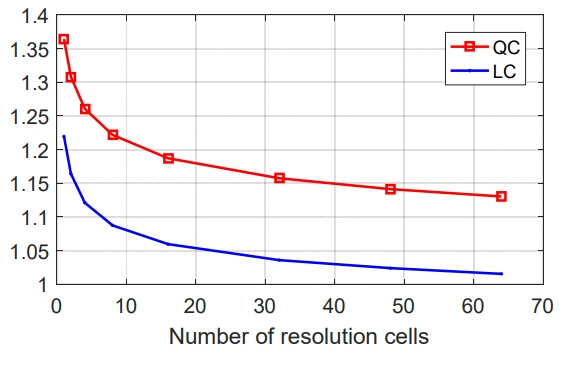
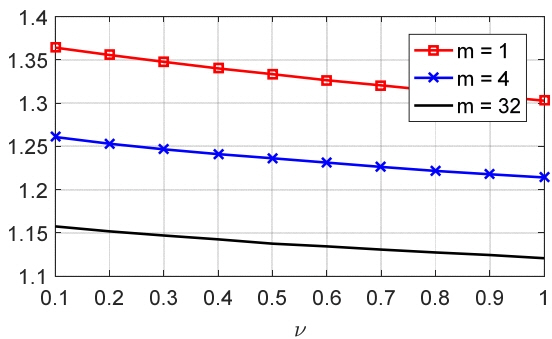
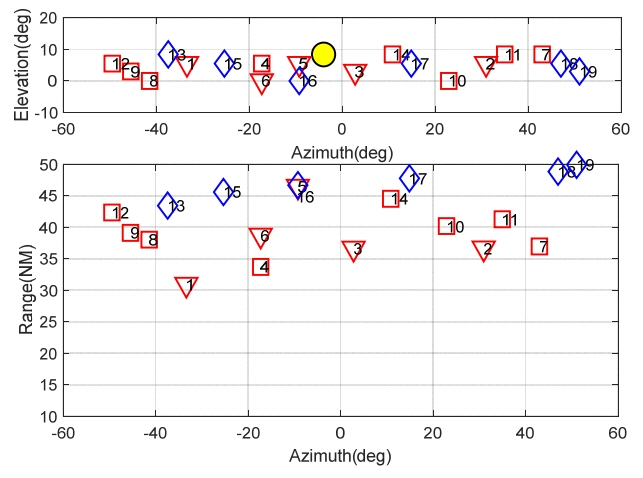
 : current beam position, ▽ : confirmed targets, □ : detected but not confirmed targets, ⋄ : undetected target).
: current beam position, ▽ : confirmed targets, □ : detected but not confirmed targets, ⋄ : undetected target).