Control of Power Distribution for Multiple Receivers in SIMO Wireless Power Transfer System
Article information
Abstract
A method to control the power distribution among receivers by the load values in a single-input, multiple-output (SIMO) wireless power transfer (WPT) system is investigated. We first derive the value of loads to maximize total efficiency. Next, a simple, but effective analytical formula of the load condition for the desired power distribution ratio is presented. The derived load solutions are simply given by system figure of merits and desired power ratios. The formula is validated with many numerical examples via electromagnetic simulations. We demonstrate that with the choice of loads from this simple formula, the power can be conveniently and accurately distributed among receivers for most practical requirements in SIMO WPT systems.
I. Introduction
A magnetically coupled wireless power transfer (WPT) system consisting of one transmitter and one receiver was successfully demonstrated using coupled-mode theory (CMT) in [1]. The WPT technology has since been studied to enable various applications, such as charging mobile phones, tablets, notebooks, home appliances, motor vehicles, and biomedical devices. The ongoing goal of researchers in this field is to achieve a higher efficiency over a longer distance. The use of an optimum load to realize the upper limit of transfer efficiencies was highlighted from the beginning [1] and has been one important design guideline in practice. To enhance the WPT efficiency beyond the upper limit, some WPT systems using relay coils and meta-material slabs have been studied [2–4].
Recently, the research interest in WPT technology has been extended to accommodate multiple-input multiple-output (MIMO) systems. In particular, the MIMO WPT [5] system has been attracting attention as a way to enable the energy autonomy of Internet of Things (IoT) sensors. For general MIMO WPT systems, the efficiencies are usually evaluated numerically using a Z-matrix circuit formulation [6]. The loads to achieve a specifically required power distribution to multiple receivers can be found numerically using a genetic algorithm. However, the exact analytic (or closed-form) solutions for them have not yet been found for a general MIMO system.
A single-input multiple-output (SIMO) system can be considered a subset of MIMO systems. The overall efficiency of a SIMO WPT system was initially examined using CMT [7]. A circuit-centric matrix analytical model that predicts the behavior of SIMO systems was also presented [8].
In addition to achieving high efficiency, power distribution among receivers has been of great interest in designing a SIMO WPT system. For example, [9] proposed a time-shared charging technique to distribute power to receivers. In an effort to reduce the coupling effects between receivers, [10] diversified the resonant frequencies among the receivers. In this method, the power division among receivers was still controlled by adjusting the charging time. The methods proposed in [11, 12] were presented in a relatively complex and abstract form to be used in design practice.
Another method to control the power distribution among receivers is to adjust the loads at the receivers. In [13], a power division was achieved by utilizing impedance inverters at the receiver sides on a two-receiver example. In [14], an impedance matching method for the power distribution among receivers was proposed based on coupled-mode and circuit theories. The actual power distribution among receivers, however, differs greatly from the desired distribution, especially in a condition of highly asymmetric distribution. [15] developed a new power control scheme by combining maximum efficiency point tracking (MEPT) with time-division multiplexing (TDM). In [16], multiple-receiver WPT-based battery voltage equalization was investigated using analytical derivations and experiments.
In this paper, we derive and present a simple analytic solution to control the power distributions among multiple receivers. The necessary receiver load values for a desired power distribution can be easily computed using the presented solution with little loss of accuracy. The proposed method of realizing arbitrarily desired power distributions is verified using numerical examples in circuit and electromagnetic (EM) simulations.
II. Modeling of a SIMO WPT System
1. Formulation of a SIMO WPT System
Fig. 1(a) and (b) show a typical SIMO WPT system and its equivalent circuit. The system is assumed to have a single transmitter and multiple receivers. All the loops (or coils) have some inductances (Li) and resistances (Ri). Each coil is loaded with a capacitor (Ci) for resonance at a specific design frequency. The transmitter is excited by a voltage source (V0), and the N receivers have load resistances (RLi) to receive transferred powers. Once the sizes and positions of the transmitter and receivers are specified, the coupling coefficients between any two loops can be determined using the ratio of magnetic flux lines from one loop to the other [17]. The WPT system can then be analyzed in terms of the efficiencies for each receiver and for the total system. For (N + 1) loops of the SIMO WPT system in Fig. 1, we can write (N + 1) equations using KVL. They can be rearranged using a Z-matrix formulation. The Z-matrix as a function frequency is given by:
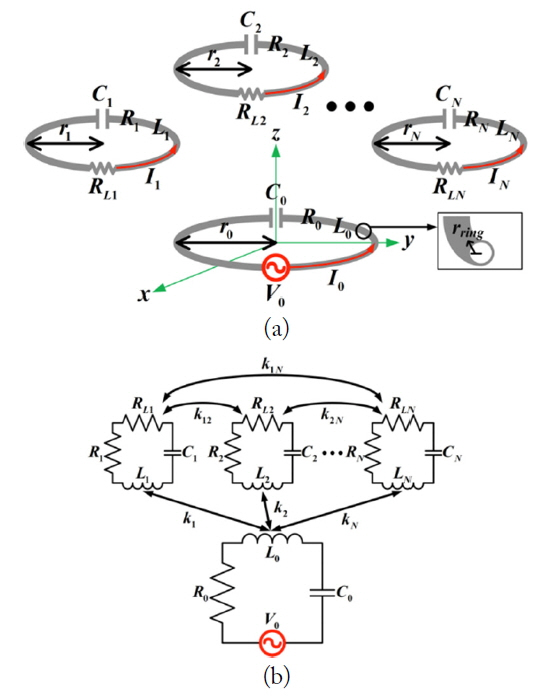
A general configuration of a SIMO WPT system with one transmitter and N receivers. (a) Geometry and (b) equivalent circuit.
In (1), V0 in the column matrix [V] is the supplied voltage of the transmitter. The principal diagonal elements of [Z] at the resonant design frequency are given by:
and
where Ris are the loop resistances and RLi’s are the load resistances for the receivers. The other elements of [Z] are given by:
where kijs are the coupling coefficients between two loops. When all the elements of the Z-matrix are given, the current on each loop is determined by [I] = [Z]−1[V], in which all couplings between any two loops including the mutual are all considered. The input power and the received power at each receiver can then be evaluated using:
and
2. Derivation of the Optimum Load and Efficiency in SIMO
The efficiency for the ith receiver at the resonant frequency is defined and expressed as:
The efficiency can be evaluated using (7) or by |Si0|2/(1-|S00|2) using EM simulations. The efficiencies using the two methods always agree well. If the coupling coefficients between any two receivers shown in Fig. 1 are negligible (kij → 0, i ≠ j for i, j = 1, 2,···, N), the ratio of the currents on the ith receiver and the transmitter is expressed in an analytic form, as in [18]:
and (7) can be simplified to:
where Fi and βi are defined as the figure of merit and the normalized load resistance defined by:
and
where ki is the coupling coefficient between the transmitter and ith receiver [17], and Qi is the quality factor of the ith receiver.
The figure of merit (10) is entirely determined by the specification of the Tx and Rx loops and the arrangement between them and is not dependent on the load RLi. The system efficiency (or total efficiency) is defined and given by:
as a function of N normalized loads.
To derive βis (i = 1, 2, ···, N), which maximize ηt in (12), we require:
The N partial differential equations must be solved simultaneously. The normalized load resistance βi for i = 1, 2,···, N satisfying (13) turned out to be identical as a constant βopt for all receivers [11], although the figures of merit (Fis) given by (10) are different. They are:
It is convenient if we define the overall figure of merit of a SIMO system (F) as:
The normalized optimum load βopt in (14) can then be simply expressed as:
With (16), the maximum of ηt in (12) can be expressed as:
after some algebraic arrangements. Notice that (16) and (17) have exactly the same forms as those for SISO systems [16]. Note that as F (15) becomes very large, the efficiency in (17) goes to 1. As F becomes very small, the efficiency goes to zero.
3. Numerical Examples with One Transmitter and Two Receivers (N = 2)
As an example, assume that we have one Tx and two Rx loops, where the figures of merit between the Tx and Rx loops are F1 = 16.2 and F2 = 10.7. The efficiency of individual Rx ηi and the total system efficiency ηt can be controlled by the (normalized) load βi. From Fig. 2, we can analyze how selectively power can be distributed to each Rx in the following scenarios.
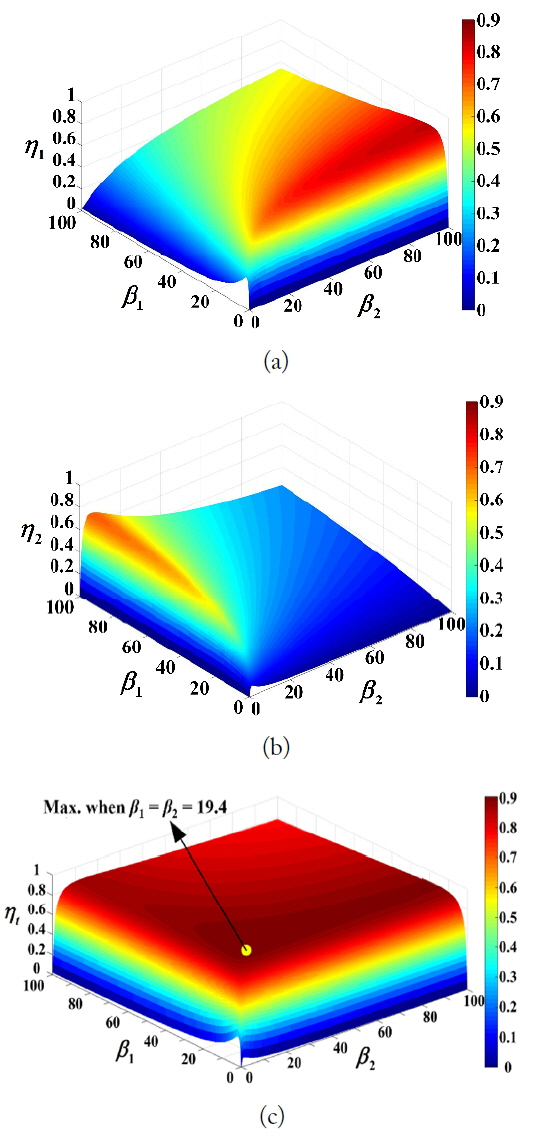
Efficiencies as a function of the normalized load resistances β1 and β2 in the SIMO system (N = 2, F1 = 16.2, and F2 = 10.7). (a) Efficiency for the 1st receiver (η1), (b) efficiency for the 2nd receiver (η2), and (c) total efficiency of the SIMO system (ηt).
In the first scenario, let us suppose we want to deliver the most power to Rx1 instead of Rx2. Intuitively, one can achieve this by opening the load of Rx2 (β2 → ∞) to suppress any power flow into Rx2 and re-direct that power to Rx1. Simultaneously, the load value of Rx1 should be optimized to receive the maximum power. This conjecture is consistent with the result in Fig. 2. Explicitly, when β1 is about 16.2 and β2 → ∞, η1 is maximized to 88.4% and η2 decreases to zero in Fig. 2(a) and (b).
The opposite is true in the second scenario in which we want to deliver the most power to Rx2 instead of Rx1. Fig. 2 shows that when β1 → ∞ (Rx1 is open) and β2 is about 10.7, η1 and η2 reach zero and 82.9%, respectively. Obviously, the maximum η1 (88.4%) is greater than the maximum η2 (82.9%) because Rx1 is inherently more strongly coupled to Tx than Rx2; F1 (= 16.2) is greater than F2 (= 10.7).
Next, one may choose to maximize the total system efficiency ηt. The maximum total efficiency in Fig. 2(c) is about 90.2% when
Another important observation from Fig. 2(c) is that over a wide region of β1 and β2, the total efficiency ηt is nearly invariant from the maximum of 90.2%. This implies the power can be distributed among multiple receivers in almost any ratio users desire, with minimum loss in total efficiency.
III. Control of Power Distribution Ratio
The choice of power delivery distribution is not limited to the three scenarios mentioned above in Section II-C. The continuous distribution of efficiencies in Fig. 2 suggests that users are allowed an infinite number of choices of power distribution to each Rx, with total efficiency nearly unchanged. In this section, we propose a simple method to determine the load resistances of receivers to control the power distribution ratio. We also demonstrate the method using numerical examples.
1. Load Resistance for Desired Power Distribution
To demonstrate the method, we first define the power distribution ratio (α1, α2, ···, αN) for the receivers as follows:
Clearly,
where αi,opt’s (for i = 1, 2,···, N) are the optimum power distribution ratio to maximize the total efficiency (12). If the desired power distribution ratio (αi’s for i = 1, 2,···, N) is different from the optimum power distribution ratio (αi,opt’s for i = 1, 2,···, N), the total efficiency may become somewhat lower than the maximum depending on the degree of the difference of the optimum (12).
In case a desired power distribution ratio (αi’s) is specified first in (18), the load values, βis, of the receivers can be obtained numerically. However, the exact analytic solution in a simple form has not been found yet.
Instead, we propose a simple, approximate solution to control the power distribution ratio. We first note that the total efficiency is insensitive to the choice of load resistances from Fig. 2(c) unless they deviate significantly from their optimum (16). Based on this observation, the ratio of (18) and (19) can be approximated as:
We further assume 1 + β ≈ β (or β >> 1), which is indeed the case for most practical WPT problems. This leads to the conclusion that to achieve the desired αi, βi is:
for i from 1 to N. The receiver load solution (21) can be used as a formula determined by only F (15), Fi (10), and the desired αi. In Sections III-B and III-C, we will show that the accuracy of (21) is high enough for most practical problems unless the desired power distribution ratio (α1, α2,···, αN) deviates too much from its optimum (F12/F2, F22/F2,···, FN2/F2) (19).
In Fig. 3, based on (21), we plot

Normalized load
For example, when F1 = 16.2 and F2 = F3 = 11.4, F = 22.9 using (15), α1,opt = F12/F2 = 0.5, α2,opt = α3,opt = 0.25 from (19), βopt = 22.9 from (14) or (16), and ηt(βopt) = 91.6% from (17). If the desired α1, α2, and α3 are 0.7, 0.2, and 0.1, we can obtain β1 = 16.4, β2 = 28.6, and β3 = 57.3 using (21) and ηt = 91% using (12).
2. Numerical Validation by Circuit Simulations (N = 2)
The proposed power distribution method was validated using circuit simulations. We physically have one Tx loop and two Rx loops, and the resonant frequencies of all of them are set to 6.78 MHz. The circuit element values (R, L, and C) are 0.034 Ω, 0.533 μH, and 1.034 nF for the Tx loop and 0.017 Ω, 0.223 μH, and 2.472 nF for the Rx loop. The quality factors of the Tx and Rx loops are 668 and 559, respectively.
The coupling coefficients between the Tx and each Rx (k1 and k2) are assumed to be identical at 0.0265; therefore, F1 = F2 = 16.2 using (10). Fig. 4(a) shows the realized (or achieved) power distribution ratios and the total efficiencies as a function of the desired α1. Note that α2 = 1 – α1.
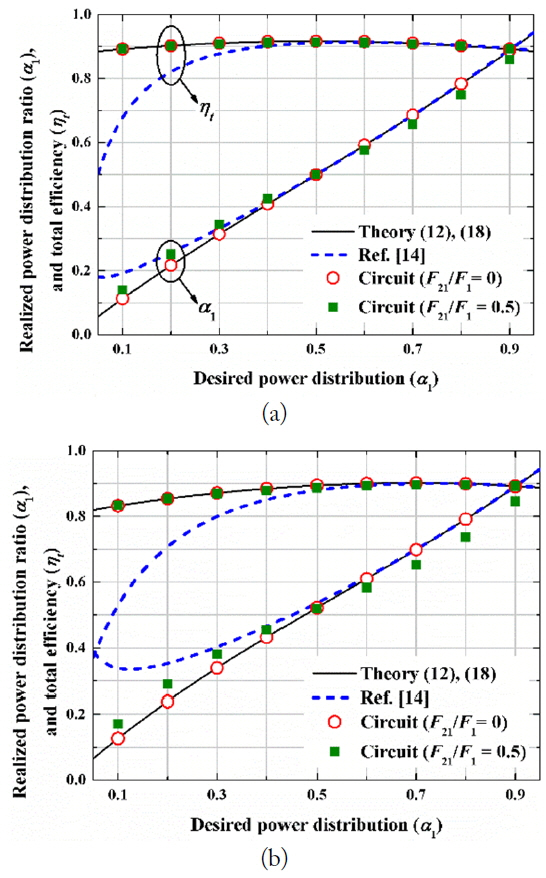
Realized α1 and ηt as a function of desired α1 (f0 = 6.78 MHz and N = 2). (a) α1,opt = F12/F2 = 0.5 = α2,opt (F1 = F2 = 16.2) and (b) α1,opt = F12/F2 = 0.7 and α2,opt = 0.3 (F1 = 16.2 and F2 = 10.7).
The optimum power distribution ratio is α1,opt = α2,opt = 0.5 ( = 16.22/(16.22 + 16.22)) from (19). When β1 = β2 = βopt = 22.9 (16), the total efficiency is maximized to ηt(βopt) of 91.64%. One can find that the power is distributed to Rx1 with an accurate ratio as we target. Fig. 4(a) also demonstrates that the closed-form formula (21) is more accurate than the formula presented in [14]. Furthermore, we can see that even when the mutual coupling between two receivers is considered with F21/F1 = 0.5, the results do not show much difference.
As an asymmetric example, the coupling coefficients between the Tx and each Rx (k1 and k2) are assumed to be 0.0265 and 0.0175. Therefore, F1 and F2 are 16.2 and 10.7. The realized power distribution ratios and the total efficiencies are shown in Fig. 4(b) as a function of the desired α1. The optimum power distribution ratio at Rx1 (α1,opt) is 0.7 using (19). When β1 = β2 = βopt = 19.4, the total efficiency is maximized to 90.21%. Unlike the first example, the realized power distribution ratio slightly deviates from the target ratio, especially when the target power distribution ratio is low. For example, when the target ratios α1 and α2 are 0.3 and 0.7, the realized ratios are about 0.34 and 0.66.
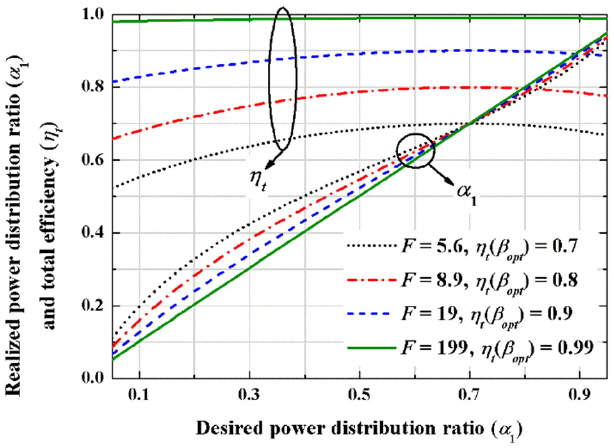
In Fig. 5, the realized power distribution ratios and total efficiencies are shown as a function of desired α1 for various maximum total efficiencies of 0.99, 0.9, 0.8, and 0.7 (17) obtained when the overall figures (F) of merit are 199, 19, 8.9, and 5.6, respectively. It is assumed that N = 2 and F12/F2 = α1,op = 0.7 for all cases. Although the accuracy of the realized power distribution ratio slightly decreases as the desired α1 deviates from its optimum, the proposed simple solution (21) is good enough for all practical applications. If a higher accuracy is required, the numerical method can be used to obtain the exact solution.
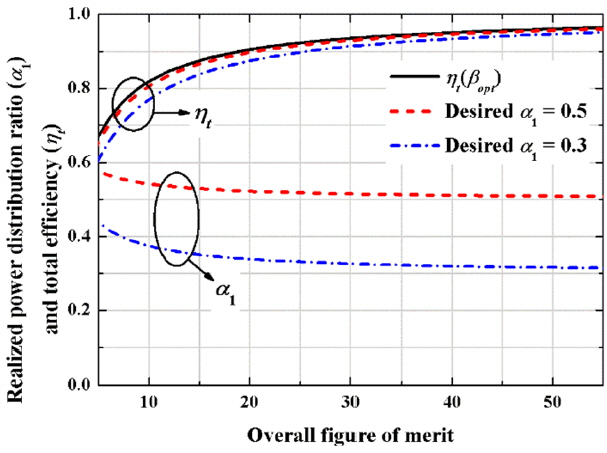
Fig. 6 shows the realized power distribution ratios and total efficiencies as a function of F (15) for different desired α1s of 0.3 and 0.5. The optimum power distribution ratio α1,opt is fixed at 0.7. The accuracy of power distribution ratio increases as F increases. This figure also demonstrates that the proposed method is good enough unless F in (15) is extremely small. Notice also that the realized total efficiency ηt (12) is only slightly lower than its maximum of ηt(βopt) (17) obtained when the desired α1 is identical to α1,opt of 0.7 (21).
3. Validation by Full Wave Electromagnetic Simulation with Three Receivers (N = 3)
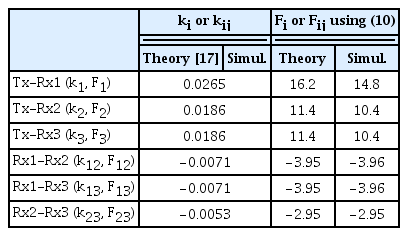
Fig. 7 shows a configuration of the SIMO WPT system with one transmitter and three receivers for the validation of the proposed solution (21) using full wave EM simulation. The resonant frequencies (f0’s) of Tx and Rx loops are 6.78 MHz. The radii of Tx and Rx loops are 10 cm and 5 cm, respectively. The radii of the loop ring are 0.2 cm. Theoretical and EM-simulated circuit element values of Tx and Rx loops are summarized in Table 1. The quality factors of the Tx and Rx loops based on EM simulations are 614 and 506 at 6.78 MHz, respectively.
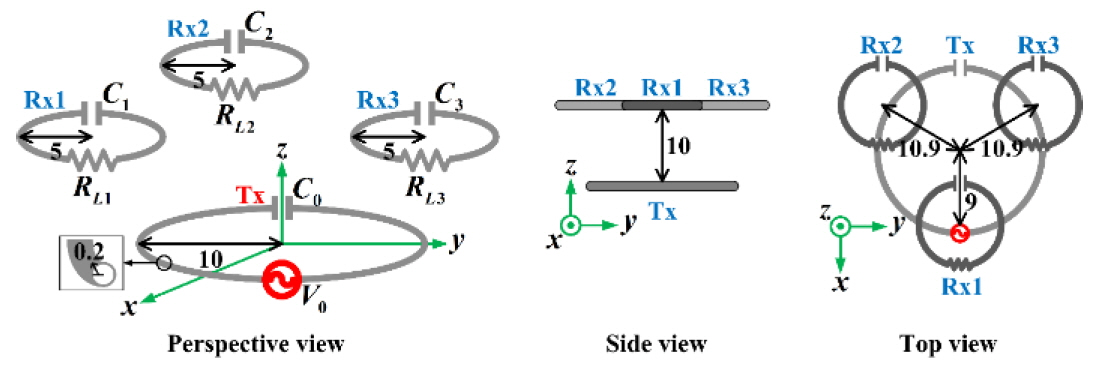
A configuration of SIMO WPT system with one transmitter and three receivers for validation by full wave EM simulation (unit: cm).
The center positions of one Tx and three Rx loops in Fig. 7 are (0 cm, 0 cm, 0 cm), (9 cm, 0 cm, 10 cm), (−5.5 cm, −9.4 cm, 10 cm), and (−5.5 cm, 9.4 cm, 10 cm), respectively. The centers of the Rx loops are 9 cm, 10.9 cm, and 10.9 cm away from the z-axis. The coupling coefficients between two loops can be theoretically evaluated using [17] and can also be extracted using the S-parameter obtained from EM simulations [19]. Figures of merit can be obtained using (10). Coupling coefficients and figures of merit between two loops are summarized in Table 2. The EM-simulated ks agree well with the theoretical ones. F1, F2, and F3 are 14.8, 10.4, and 10.4, respectively, using (10). For this example, α1,opt = F12/F2 = 0.5 and α2,opt = α3,opt = 0.25 from (19).
Fig. 8(a) and (b) show the necessary load resistances (RLis) using (21) based on Tables 1 and 2 to realize a desired power distribution ratio (αis) based on the assumptions of α2 = α3 and α2 = 2α3, respectively. Note that for each case, α1 + α2 + α3 = 1. As we can see in (21), RLi decreases as the desired αi increases.
When the desired α1, α2, and α3 are 0.5, 0.25, and 0.25 in Fig. 8(a), the load resistances (RL1, RL2, and RL3) are the optimum values (RL,opts) (16), which are about 0.39 Ω.
Fig. 9 shows the realized power distribution ratios and the total system efficiencies of the same SIMO system used in Fig. 8 using theory based on (12) and (18), EM-simulation with RLi, and EM simulation with and additional feeding loop (50 Ω) [20].
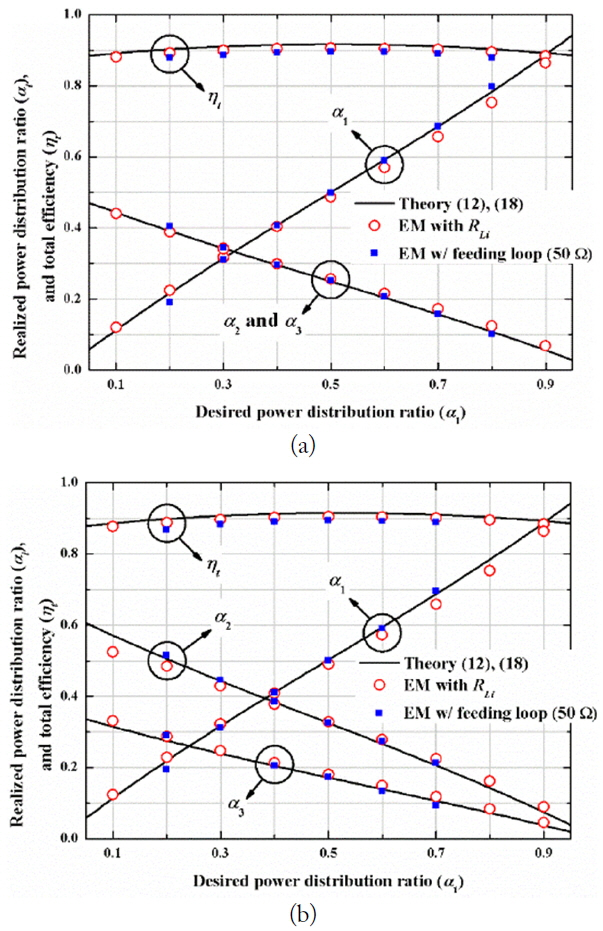
Realized α1 and ηt as a function of desired α1 (f0 = 6.78 MHz, N = 3, r0 = 10 cm, r1 = r2 = r3 = 5 cm, rring = 0.2 cm, α1,opt = 0.5, and α2,opt = α3,opt = 0.25). (a) α2 = α3 assumed, (b) α2 = 2α3 assumed.
In Fig. 9(a), they have been plotted as a function of the desired α1, with α2 = α3. For this case, the maximum efficiency is 91.6%, and realized power distribution ratios are shown to be almost the same as the desired ones. Again, we can see that the realized αis agree well with the desired ones for all cases.
Similarly, the realized αis and total efficiency are plotted as a function of the desired α1, with α2 = 2α3 in Fig. 9(b). We can also see that the αis are well realized, as we desire. For example, when the desired α1, α2, and α3 are 0.7, 0.2, and 0.1, respectively, they are realized as 0.69, 0.2, and 0.11. The results of EM simulations without and with a feeding loop [20] are also shown to be in good agreement with the results of circuit simulations.
Finally in Fig. 10, we show the EM-simulated |Hz| distributions for the cases of desired α1 = 0.5 and α2 = α3 = 0.25 and desired α1 = 0.7, α2 = 0.2, and α3 = 0.1. For these field distributions, a power source of 1 W was used in HFSS EM simulations. The |Hz| field distributions in Fig. 10(a) and (b) well reflect the desired power distributions or efficiencies. The total efficiencies and power distribution ratios based on theory and EM simulations are in good agreement.
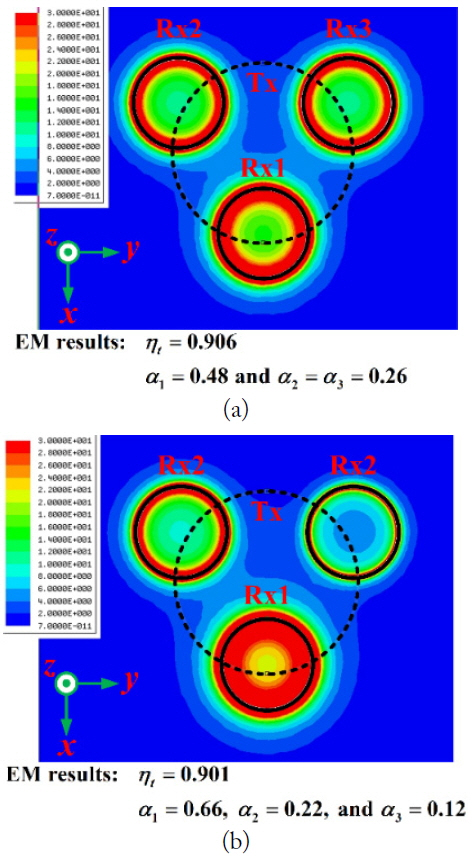
EM-simulated |Hz| distribution (f0 = 6.78 MHz, N = 3, r0 = 10 cm, r1 = r2 = r3 = 5 cm, rring = 0.2 cm, α1,opt = 0.5, α2,opt = α3,opt = 0.25, βopt = 22.9, and ηt(βopt) = 0.916). (a) Desired α1 = 0.5, α2 = α3 = 0.25, and ηt = 0.916, (b) desired α1 = 0.7, α2 = 0.2, α3 = 0.1, and ηt = 0.91.
In summary, the realized αis using the simple closed-form solution (21) show good agreement with the desired ones for a wide range of applications.
IV. Conclusion
In this paper, we analyzed the efficiencies and power distribution ratio among receivers of the SIMO system consisting of multiple receivers. The optimum load for maximum total efficiency was derived using the equivalent circuit. In addition, we obtained the simple formula of the load condition for the desired power distribution ratio. We employed various numerical examples and validated the derived formula by comparing the target distribution ratio with the realized one from circuit and EM simulations. The proposed simple formula can also be applied to arbitrary N receivers. There have also been some analytical or closed-form solutions, but their accuracy is far lower than the proposed solution. The proposed formula is expected to be implemented in future SIMO industrial applications due to its simple but relatively accurate property.
Acknowledgments
This work was supported by Institute for Information & Communications Technology Promotion (IITP) grant funded by the Korea government (MSIT) (No. IITP-2018-2016-0-00291, Information Technology Research Center).
References
Biography
Gunyoung Kim received a B.S. degree in Radio Communication Engineering from Kyung Hee University, Yongin, Korea in 2010, an M.S. degree in Electronics and Radio Engineering from Kyung Hee University in 2012, and a Ph.D. degree in Electronics Engineering from Kyung Hee University in 2018. Currently, he is a post-doctor in the College of Electronics and Information at Kyung Hee University. His fields of research include microwave antennas, passive devices, wireless power transmission, and metamaterials.

Sanghoek Kim received B.S. degree with a double major in Electrical Engineering and Mathematics from Seoul National University, Seoul, Korea in 2007 and the M.S. and Ph.D. degrees in electrical engineering from Stanford University, CA, USA in 2013. His research focuses on applications of radio-frequency technology and electromagnetics theory in wireless power transfer, communications, and signal integrity in high-speed channels. After graduating, he worked at Qualcomm Inc. as a signal/power integrity engineer and at SiBeam, Inc. as a mmWave system engineer. Currently, he is an assistant professor in the Department of Electronics Engineering at Kyung Hee University.

Seunghyun Boo received a B.S. in Electronics Engineering from Kyung Hee University, Yongin, Korea, in 2017. He is currently working toward an M.S. in Electronics Engineering from Kyung Hee University. His fields of research include microwave antennas, passive devices, and wireless power transmission.

Bomson Lee received a B.S. degree in Electrical Engineering from Seoul National University, Seoul, Korea, in 1982. From 1982 to 1988, he was with the Hyundai Engineering Company Ltd., Seoul, Korea. He received M.S. and Ph.D. degrees in Electrical Engineering from the University of Nebraska, Lincoln, NE, USA in 1991 and 1995, respectively. In 1995, he joined the faculty at Kyung Hee University, where he is currently a professor in the Department of Electronics Engineering. From 2007 to 2008, he was the chair of the technical group for microwave and radio wave propagation in the Korea Institute of Electromagnetic Engineering & Science (KIEES). In 2010, he was Editor-in-Chief of the Journal of the Korean Institute of Electromagnetic Engineering and Science. From 2015 to 2016, he was vice-chairman of KIEES. In 2017, he was executive vice-chairman of KIEES. Since 2018, he has been president of KIEES. His research interests include microwave antennas, RF identification (RFID) tags, microwave passive devices, wireless power transfer, and metamaterials.