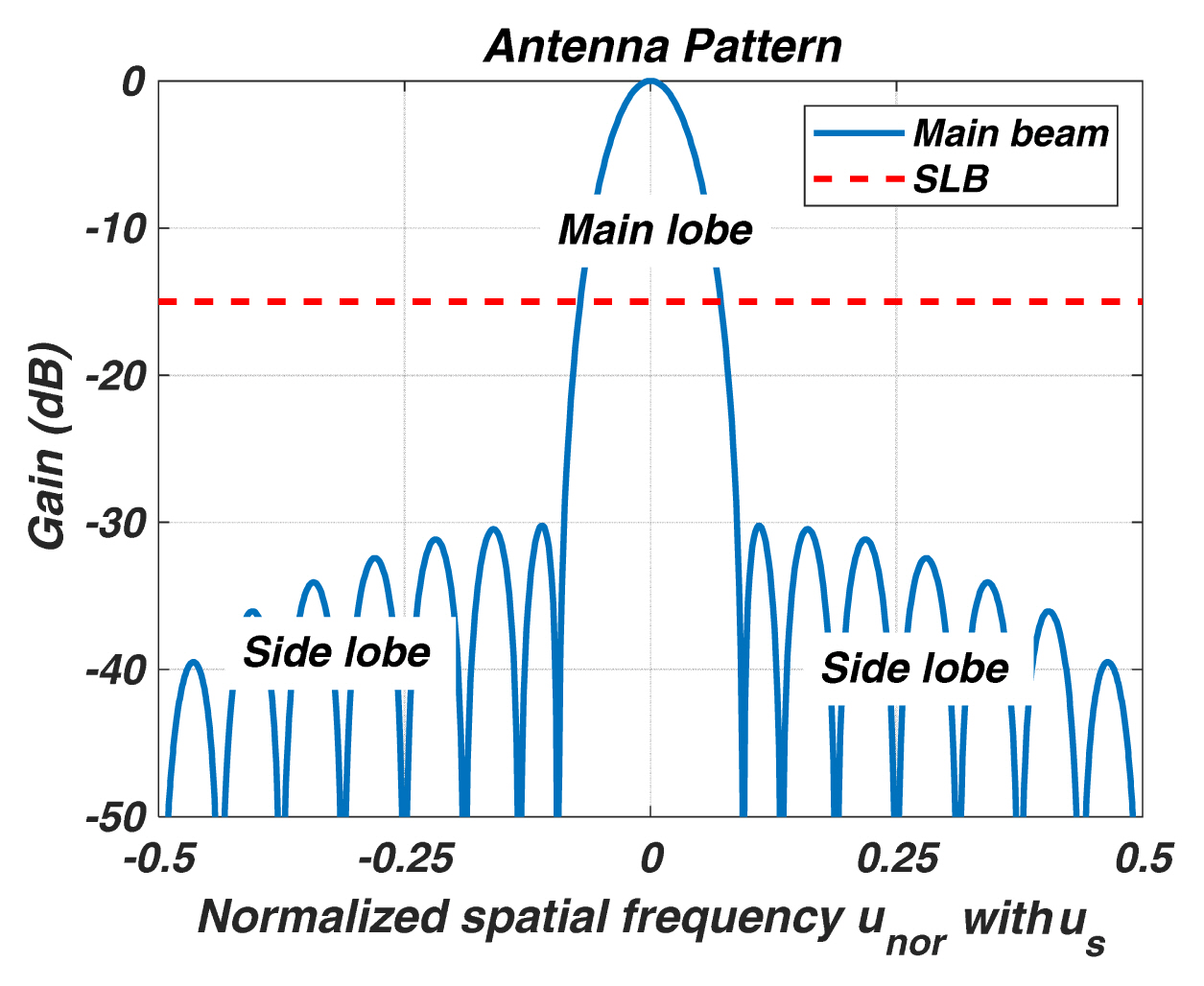
I. Introduction
II. Adaptive SLB Channel Synthesis
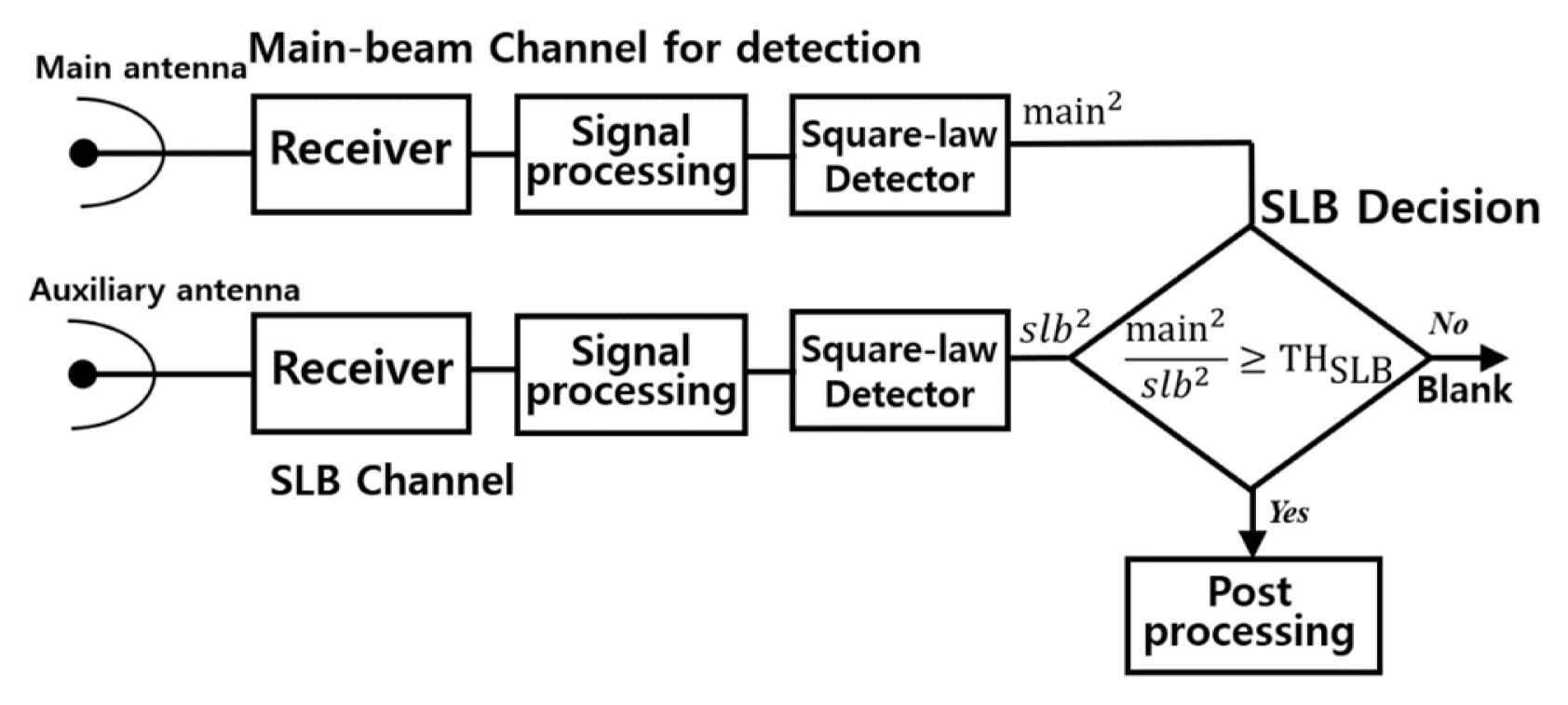
1. Conventional SLB System
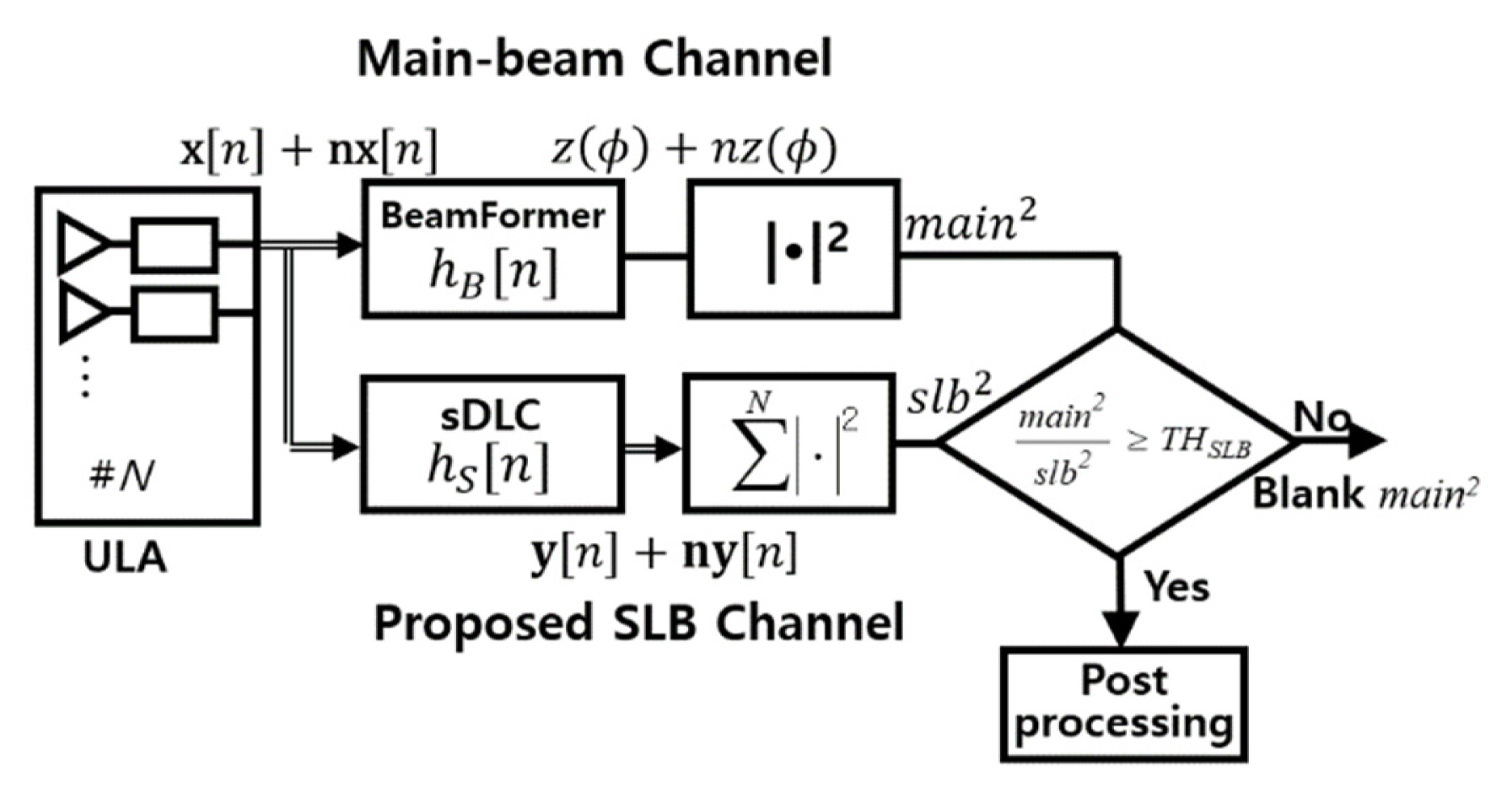
2. Adaptive SLB System with Spatial DLC and Non-coherent Integrator
III. SLB-Ratio Function for SLB Decision
1. Impulse Response and Frequency Response of the SLB System
(8)
(12)
-
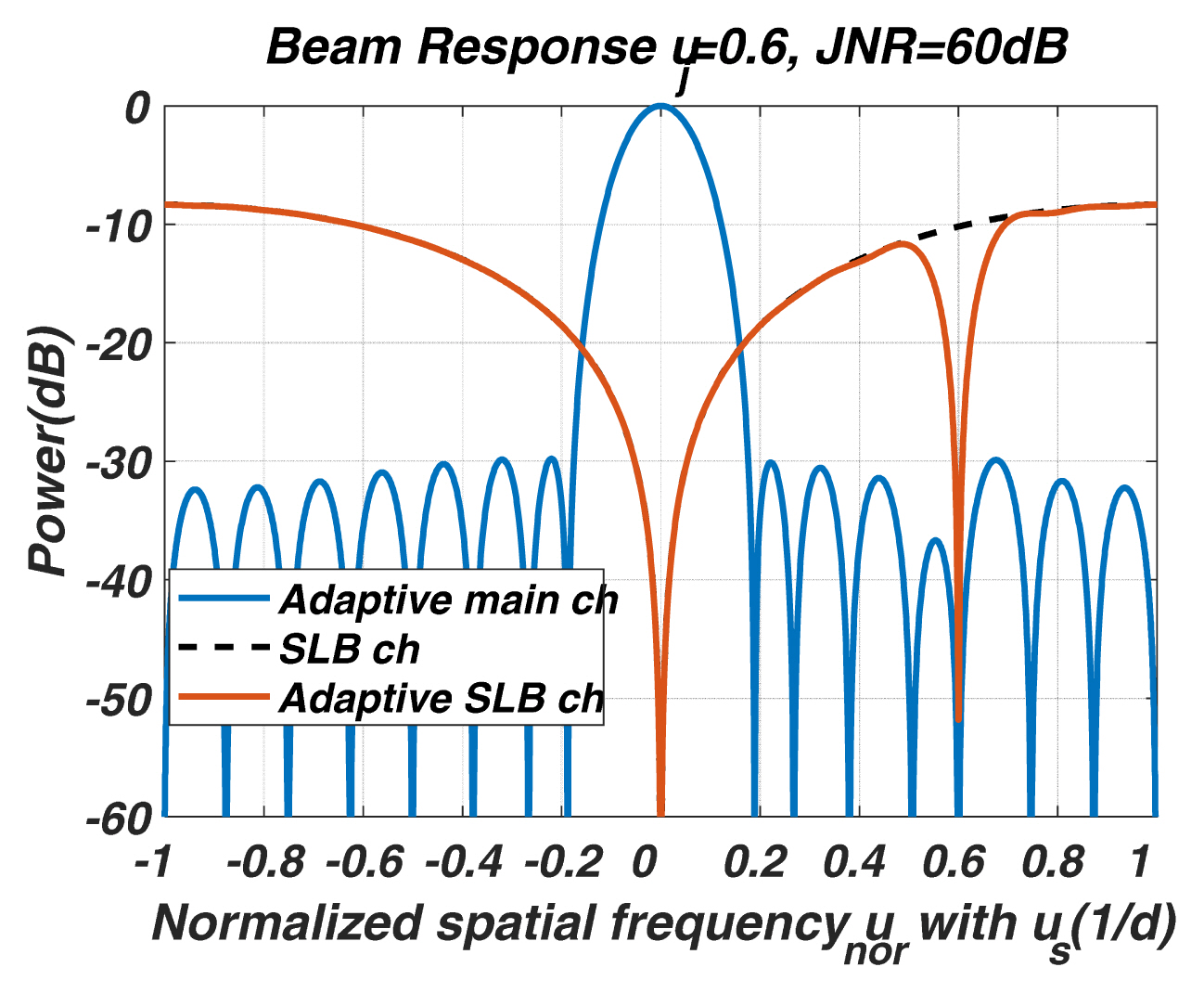
We designed the M-length of hx[n] to extract the desired spatial frequency-selective response, for example, the directivity and the null. Thus, the number of valid output samples depends on the M. If M is greater than the number of input samples N, we cannot obtain the valid output with the designed frequency-selective response of M Ōēż N, which is a necessary condition for Fig. 4. In the spatial DLC in the SLB channel, the output y[n] has valid output samples of N-1, n = 1,..., N-1, since hS[n] satisfies the causality of the first difference operation and is 2-length in Eq. (2). In the case of the beamformer in the main beam channel, for Nlength hB[n], the only N-1th output is valid:
The output with one sample no longer has a variable of n in the spatial domain, and is related to the spatial frequency response at ui, as in Eq. (13). If the input of the FIR system is a complex exponential, as in Eqs. (5) and (12), the Hx(ui) in the output is referred to as the steady-state response of the system [14]. It represents the spatial frequency response at ui in steady state, such as a pass-band or a stop-band. In addition, the steady state indicates holding its frequency response for all observations [14ŌĆō16]. Consequently, the Hx(u) with the input-complex-exponential must persist for n of any output. In particular, the steady state response Hx(u) has no more statistical meaning, such as averaging over n. On the other hand, the first term in Eq. (12), representing the value of the current input sample, becomes only a factor for scaling the amplitude and shifting the initial phase independent of the system response. Therefore, it is regarded as an ignorable complex constant of the system response.
2. Target Signal
Žāt: RCS or amplitude of the target,
ut = sin(Žåt)/╬╗ : spatial frequency of the target,
Žåt: arriving angle of the target.
3. Noise Signal
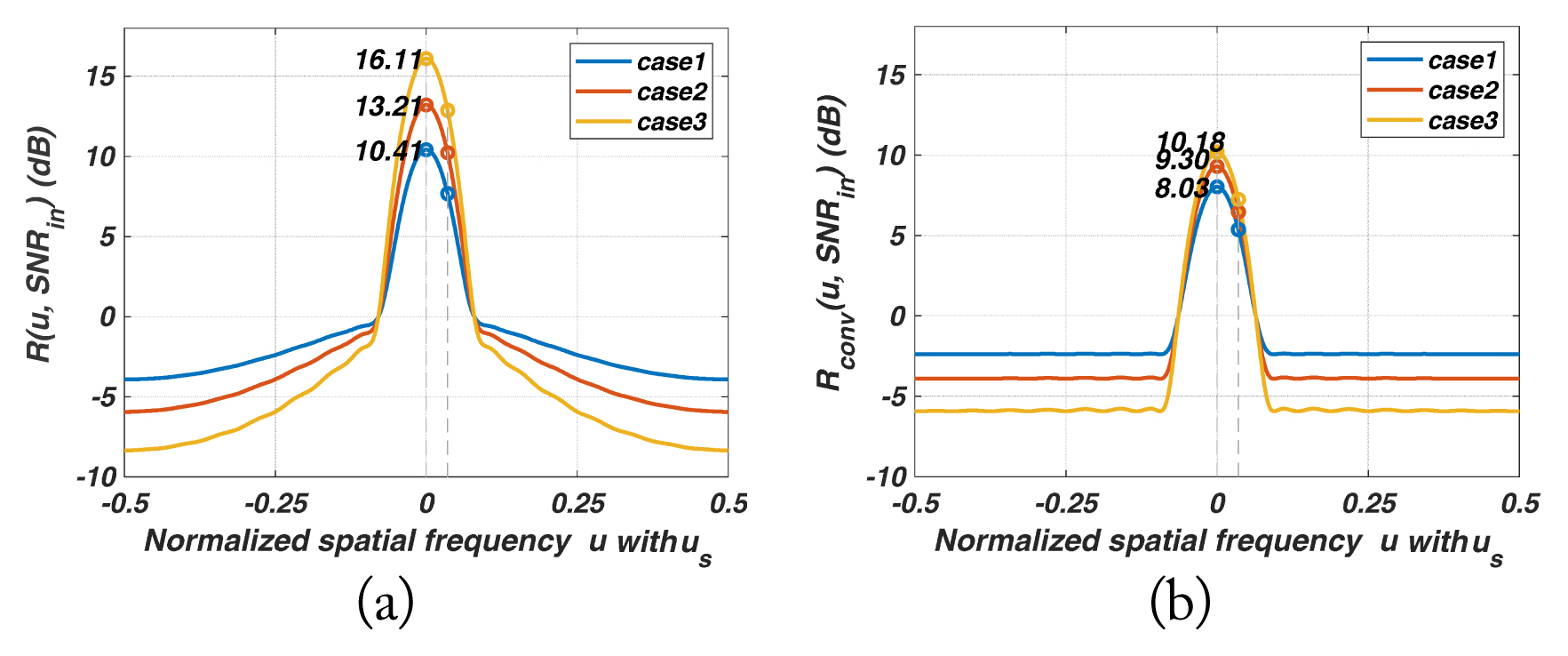
4. Input/Output SNR and SLB-Ratio Function
IV. Optimal SLB Threshold and Simulation Results
1. SLB Thresholds Appropriate for the Targets
2. Simulation Results
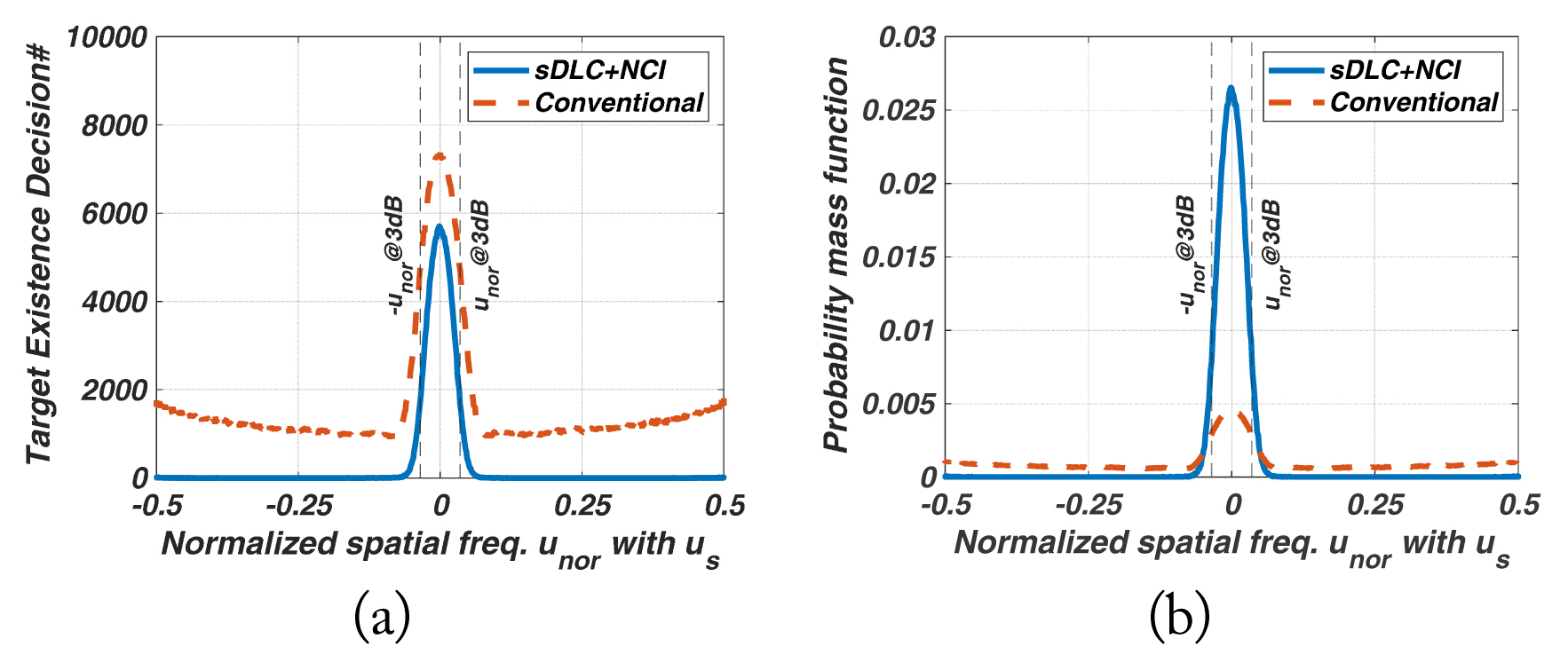
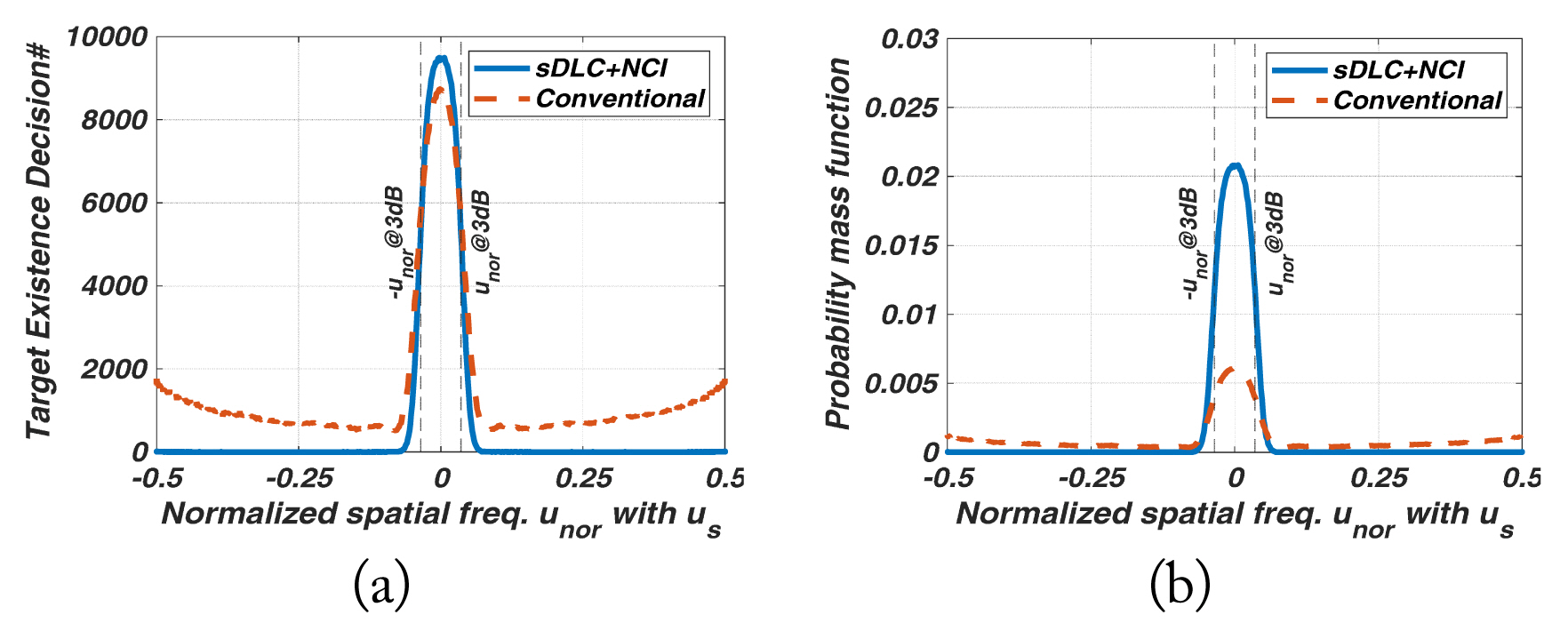
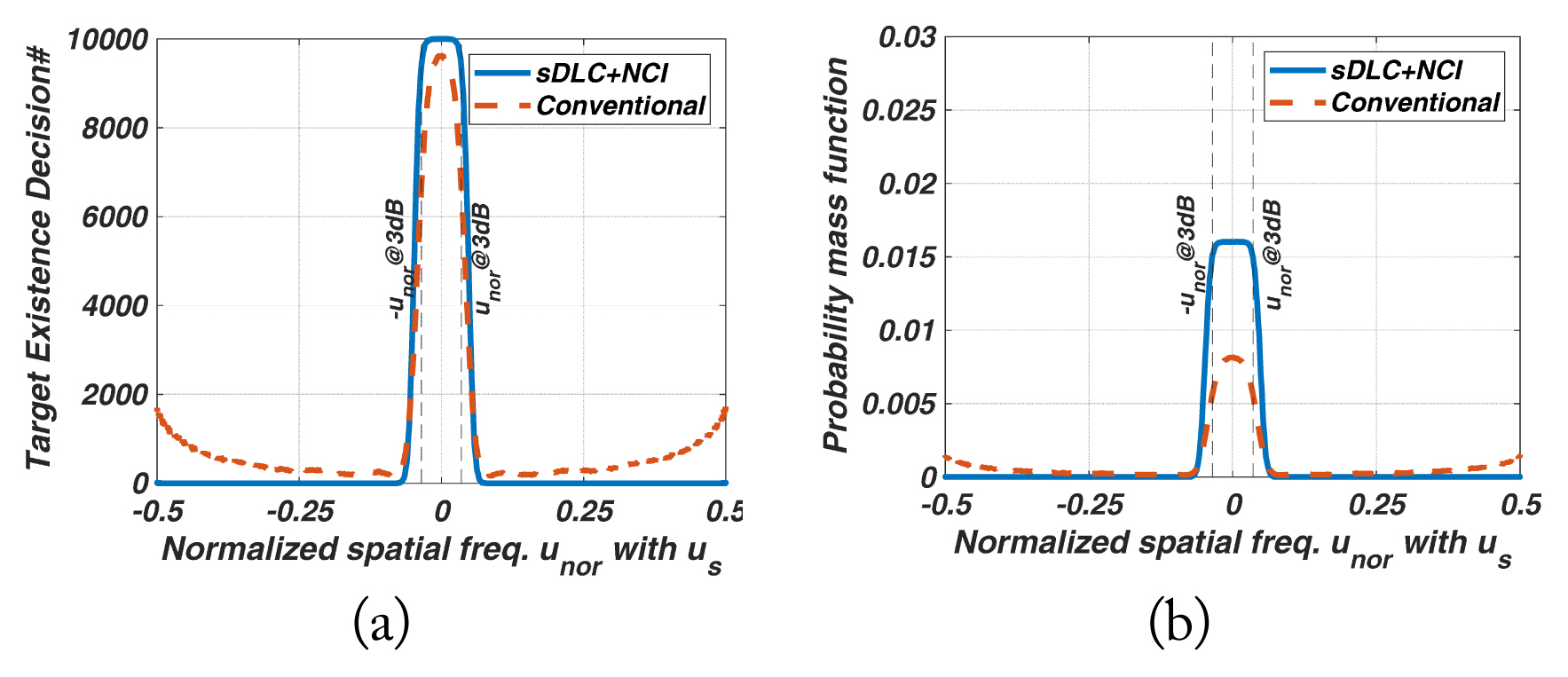
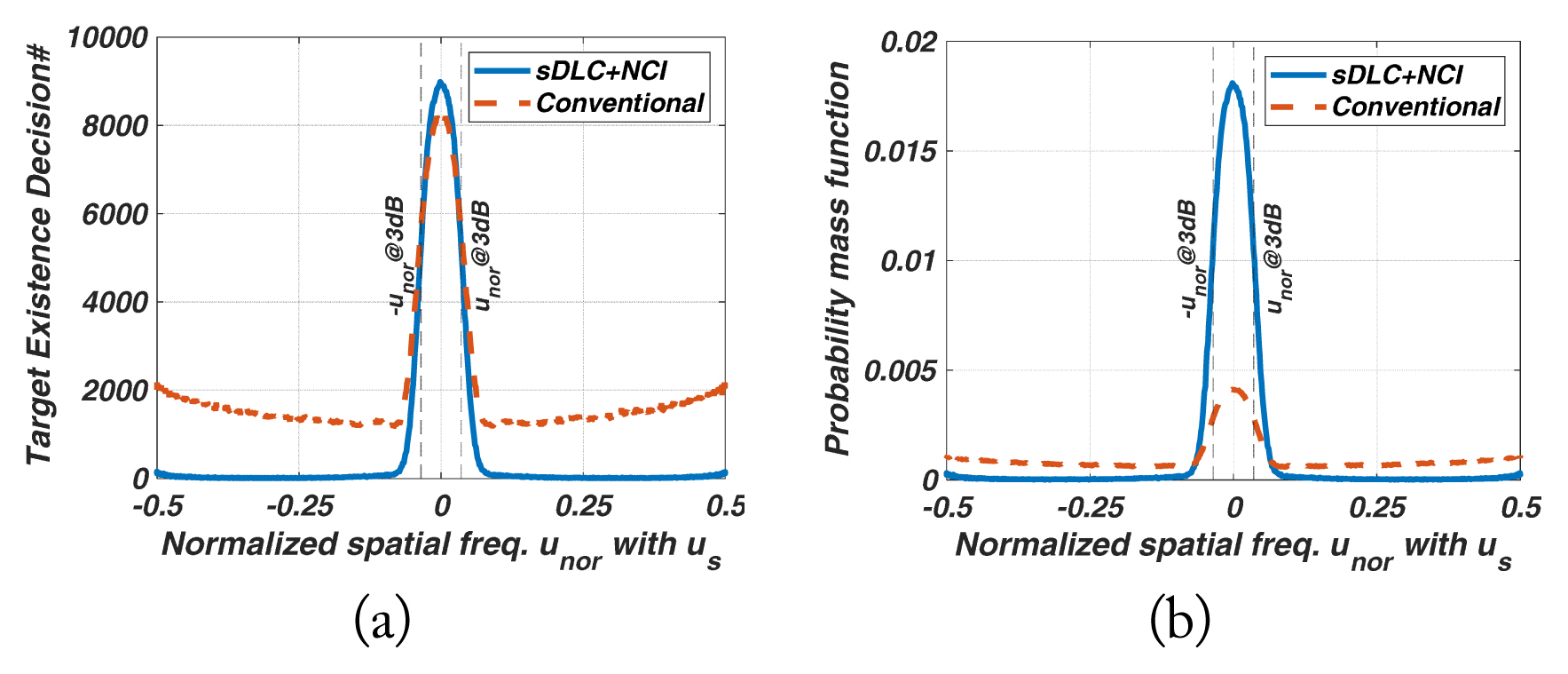
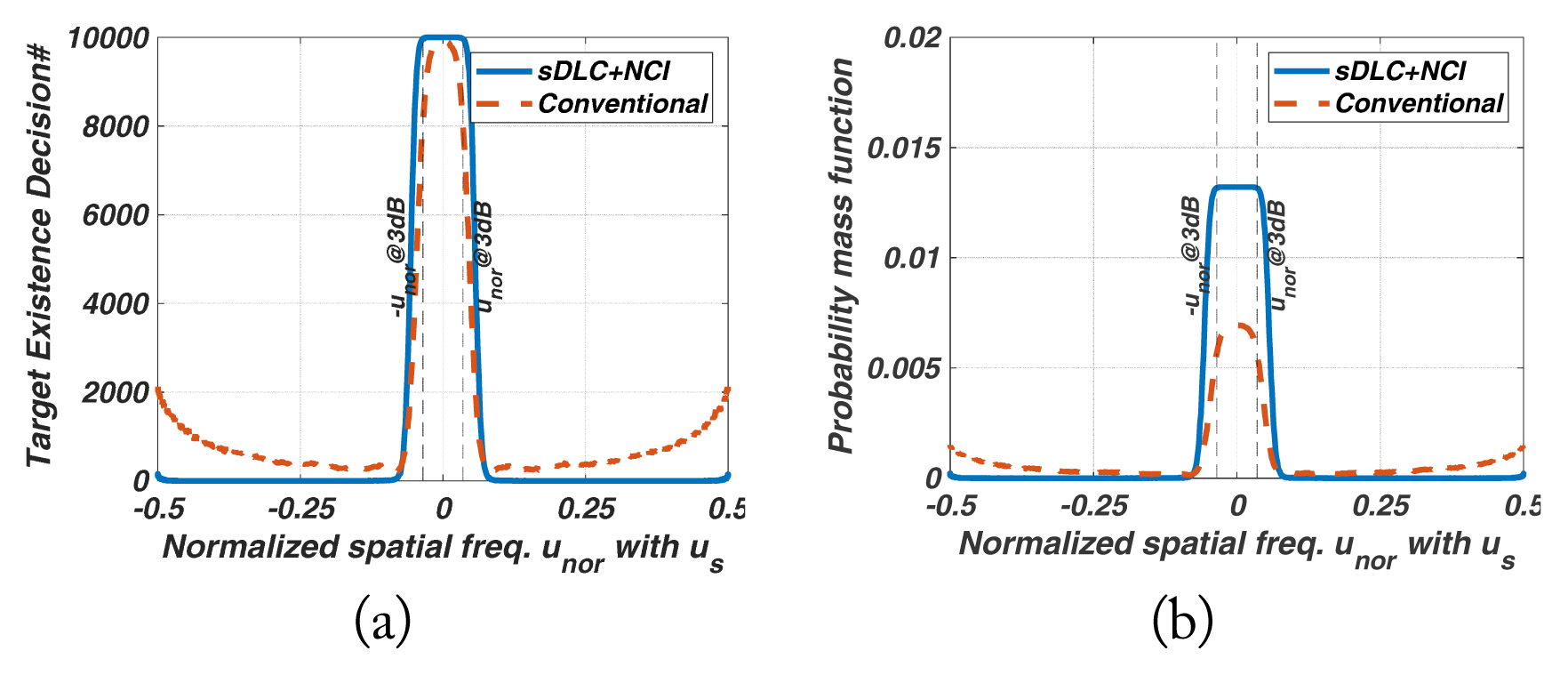
The amount of ŌĆ£Target Existence Decision#ŌĆØ within ┬▒u3dB represents the detectability of the target-in-mainlobe in the detection region, meaning the frequency of a target-in-mainlobe decision occurring in the mainlobe. If this value is low, many of the target-in-mainlobes are blanked by SLB, thus reducing the detection probability of a radar.
The distribution of the probability mass function identifies the region where the decision probability of the mainlobe target occurs intensively.
The partial sum of the probability mass function within ┬▒u3dB involved a reliability in the detection region relative to the entire u domain. This is an important indicator of a low-RCS target because an improper SLB threshold or an insufficient SLB ratio can frequently blank the target with low SNRmain in the detection region. Thus, we have displayed the quantities in tabular form. Additionally, an unfavorable SLB ratio and SLB threshold of a low-RCS target are inherently difficult when it comes to satisfying overall performance. Hence, a reasonable threshold may be acceptable. Although there is a disadvantage of low detectability of ŌĆ£Target Existence Decision#ŌĆØ in the detection region, it is sufficient to satisfy fewer blanking errors and high reliability in the detection region. Nevertheless, in the proposed method, an appropriate threshold exhibits superior detectability with high reliability in the detection region.
The remaining partial sum within the ┬▒u3dB involved a blanking error in the blanking-region: