FDTD Analysis of Electromagnetic Wave Propagation in an Inhomogeneous Ionosphere under Arbitrary-Direction Geomagnetic Field
Article information
Abstract
The finite-difference time-domain (FDTD) model was developed to analyze electromagnetic (EM) wave propagation in an inhomogeneous ionosphere. The EM analysis of ionosphere is complicated, owing to various propagation environments that are significantly influenced by plasma frequency, cyclotron frequency, and collision frequency. Based on the simple auxiliary differential equation (ADE) technique, we present an accurate FDTD algorithm suitable for the EM analysis of complex phenomena in the ionosphere under arbitrary-direction geomagnetic field. Numerical examples are used to validate our FDTD model in terms of the reflection coefficient of a single magnetized plasma slab. Based on the FDTD formulation developed here, we investigate EM wave propagation characteristics in the ionosphere using realistic ionospheric data for South Korea.
I. Introduction
It is of great importance for radio and satellite communication to study electromagnetic (EM) wave propagation in the atmosphere. However, it is not easy to investigate EM wave propagation in the ionosphere because of ionized ions and free electrons [1]. Three key parameters to consider for EM analysis of the ionosphere are plasma frequency, cyclotron frequency, and collision frequency [1]. Plasma frequency is oscillation frequency, which is related to electron movement to neutralize locally biased space. Cyclotron frequency is angular frequency of electrons when they move in circular form under a static geomagnetic field. Collision frequency is the effective number of collisions per second.
In this study, we develop a finite-difference time-domain (FDTD) [2] model suitable for EM analysis of the ionosphere, based on a simple and accurate auxiliary differential equation (ADE). Our model can accurately investigate EM wave interaction with the ionosphere because it can take into account arbitrary geomagnetic field and inhomogeneous ionospheric parameters varying in height, unlike previous FDTD studies [3]. The proposed ADE-FDTD model is validated by analyzing a simple slab of magnetized plasma. We examine EM wave interaction with the ionosphere based on realistic ionospheric data for South Korea.
II. 1-D FDTD Formulation
EM interaction with magnetized plasma can be analyzed using Maxwell’s equations coupled with the Lorentz equation of motion [1]. The governing equation set is given by the following:
Here, E is the electric field, H is the magnetic field, J is the current density, v is the collision frequency, ωp is the plasma frequency, ωb is the cyclotron frequency, and ɛ0 and μ0 are the permittivity and permeability of free space, respectively. For simplicity and without loss of generality, we assume that the EM wave propagates along the z-axis. By using the central difference scheme in both time and space [4], one can obtain
where the superscript and the subscript refer to the time indexing and the spatial indexing, respectively. Note that
III. Numerical Examples
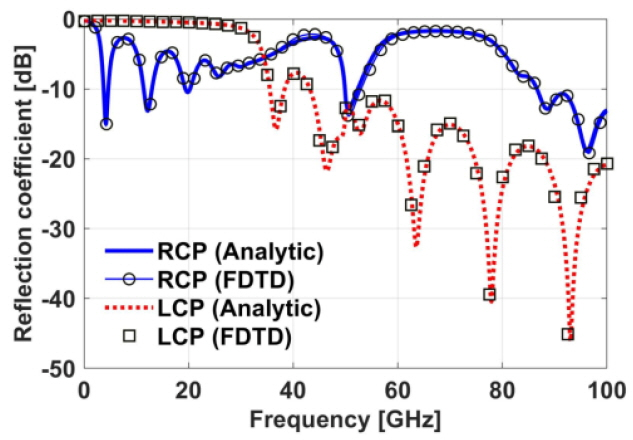
In order to validate the accuracy of the proposed FDTD model, we compute the right-hand circularly polarized (RCP) and left-hand circularly polarized (LCP) reflection coefficient of the EM wave in the magnetized plasma slab with an arbitrary angle θ between the wavenumber vector and the bias magnetic field. The ionosphere slab occupies 120 cells in the free space, and the incident wave is a differentiated Gaussian pulse. The spatial size and time step are 75 μm and 0.125 ps, respectively. The plasma parameters are ωp = 2π ×50 × 109 rad/s, ωb = 3 × 1011 rad/s, v = 20 GHz, and θ = 20°. As shown in Fig. 1, the results of the proposed FDTD model have good agreement with the analytic results [1].
Next, we examine realistic EM wave propagation characteristics using ionospheric data for South Korea. Before proceeding, it is worth explaining the key ionospheric parameters. The plasma frequency is
Here, T and Nm are ion temperature (K) and the density of molecules (per cm3) [1].
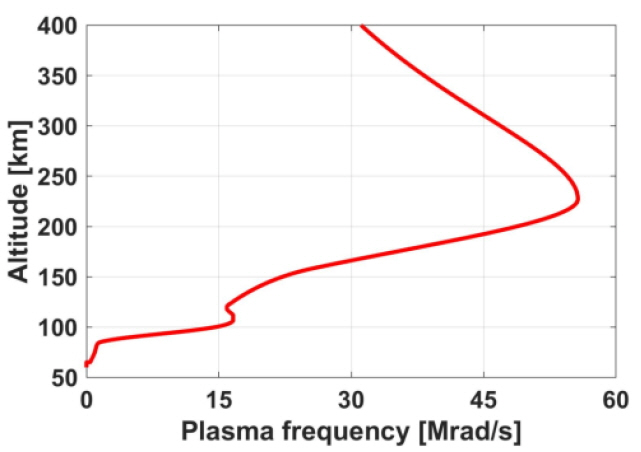
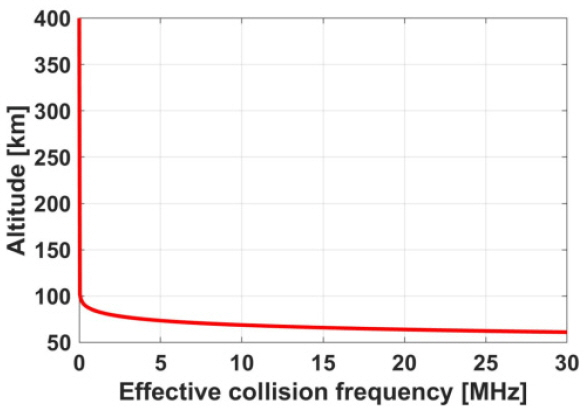
Let us consider EM wave propagation in a realistic ionosphere. For example, in this study, we consider ionospheric parameters at latitude 37°N and longitude 127°E (South Korea) on January 1, 2016. For ωp and veff, we refer to ionospheric data (ne, T, and Nm) from the Community Coordinate Modeling Center (https://ccmc.gsfc.nasa.gov/). Figs. 2 and 3 show the profiles of the plasma frequency and the effective collision frequency versus altitude. For the static geomagnetic field B, data provided from the Korea Space Weather Center (http://space-weather.rra.go.kr/) are used. It is worth noting that B hardly changes with altitude, and thus constant B is applied. Each component of cyclotron frequency, ωbx, ωby, and ωbz, is 5.21 × 106 rad/s, −7.74 × 105 rad/s, and 7.18 × 106 rad/s, respectively.
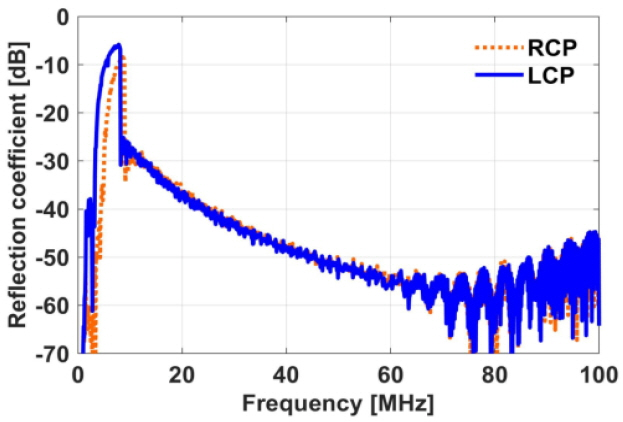
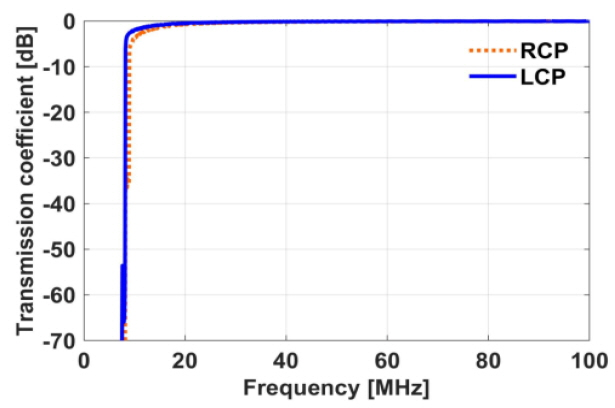
Figs. 4 and 5 show the reflection and transmission coefficients for the whole ionosphere from 50 km to 400 km. Note that the spatial size and the time step size are set as 0.3 m and 0.99 ns, respectively. For both polarizations, the reflection coefficient is largest at approximately 9 MHz, while the EM wave cannot propagate through the ionosphere considered in this study below 9 MHz.
IV. Conclusion
We provide an FDTD model suitable for the analysis of EM interaction with realistic ionosphere where EM parameters vary with altitude. For this purpose, we developed an accurate FDTD algorithm for an inhomogeneous ionosphere with arbitrary geomagnetic field, and we employed ionospheric data at a specific location and time. It is believed that the proposed FDTD model can be applied to accurately predict EM wave propagation in the atmosphere for radio and satellite communication at any location and at any time.
Acknowledgements
This work was supported by the research fund of Signal Intelligence Research Center, supervised by Defense Acquisition Program Administration and Agency for Defense Development of Korea.